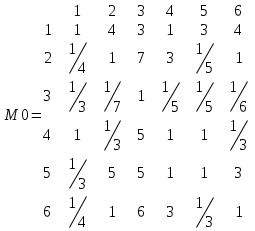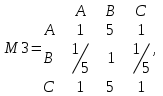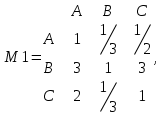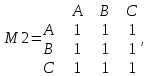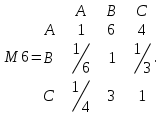Система и поддержка принятия решений лаба 1. Отчет. Метод анализа иерархий (маи) по курсу Компьютерные системы поддержки принятия решений

• Название: Метод анализа иерархий (маи) по курсу Компьютерные системы поддержки принятия решений
• Анкор: Система и поддержка принятия решений лаба 1
• Дата: 26.12.2022
• Размер: 100.62 Kb.
• Имя файла: Отчет.docx
• Тип: Лабораторная работа; #864481

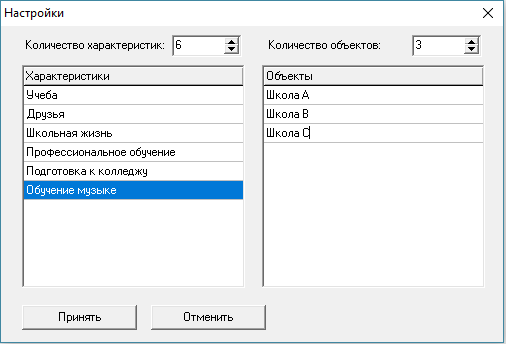
Отчет

Лабораторная работа №1

Тема: Метод анализа иерархий (МАИ)

по курсу «Компьютерные системы поддержки принятия решений»

Цель: Изучение метода анализа иерархий для поддержки принятия решений.

Ход работы:

Этап 1.

Решение задачи альтернативного выбора с помощью программной системы.

Практическое освоение МАИ в лабораторной работе начинается с простой задачи выбора школы.

Был проведен анализ трех школ А, В, С по шести критериям:

1. учеба;

2. друзья;

3. школьная жизнь;

4. профессиональное обучение;

5. подготовка к колледжу;

6. обучение музыке.

В качестве матрицы парных сравнений важности используемых критериев на этом этапе предлагается использовать следующую матрицу:

.

Номера столбцов и строк матрицы М0 совпадают с номерами критериев

Оценки школ относительно шести критериев представлены матрицами М_i i=[1,6].














Запуск программы осуществляется инициированием исполняемого файла mai3.exe в ОС Windows.

Дальнейшая работа с программой объясняется после инициирования окна «Настройки»



Шаг №1

Выберем и нажмем на кнопку «Настройки»



Заполним матрицу попарных значений для характеристик:



Заполним матрицу попарных значений для объектов:

1. учеба;

2. друзья;

3. школьная жизнь;

4. профессиональное обучение;

5. подготовка к колледжу;

6. обучение музыке.

Нажмем на кнопку «Расчет»

Результат:



Приступаем к Этапу №2

Этап 2. Проверка найденных решений с помощью таблицы Excel.

Этап 2. С помощью таблицы Excel, используя соотношение (1) и табл.1, а также методику оценки согласованности локальных приоритетов (раздел 4) проверить полученные результаты.

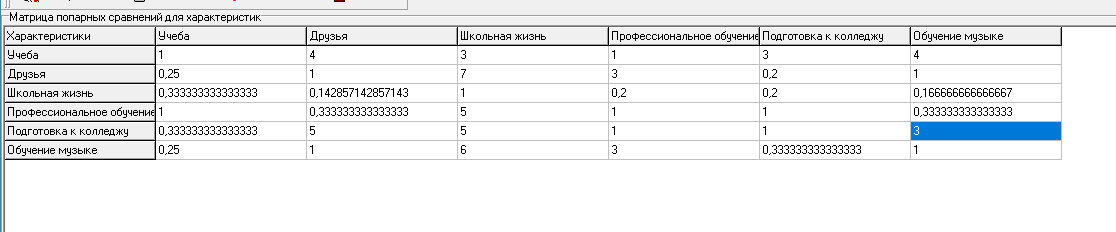
Матрица парных сравнений важности используемых критериев:
n-характеристика	1	2	3	4		5		6
1	1	4	3	1		3		4
2	0,25	1	7	3		0,2		1
3	0,333333333	0,142857143	1	0,2		0,2		0,166667
4	1	0,333333333	5	1		1		0,333333
5	0,333333333	5	5	1		1		3
6	0,25	1	6	3		0,333333333		1

Оценки школ относительно шести критериев:

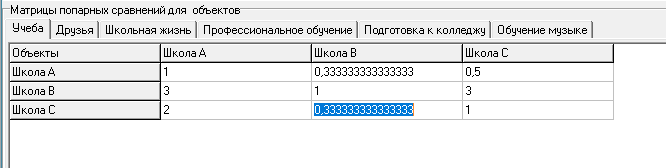
Критерий	Объект	Школа A	Школа B	Школа C
M1	Школа A	1	0,333333333	0,5
	Школа B	3	1	3
	Школа C	2	0,333333333	1
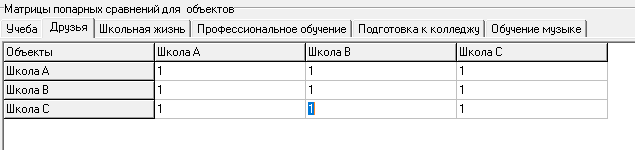
M2		Школа A	Школа B	Школа C
	Школа A	1	1	1
	Школа B	1	1	1
	Школа C	1	1	1
M3		Школа A	Школа B	Школа C
	Школа A	1	5	1
	Школа B	0,2	1	0,2
	Школа C	2	5	1
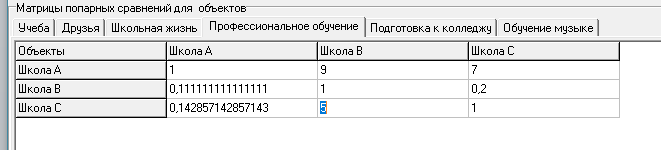
M4		Школа A	Школа B	Школа C
	Школа A	1	9	7
	Школа B	0,111111111	1	0,2
	Школа C	0,142857143	5	1
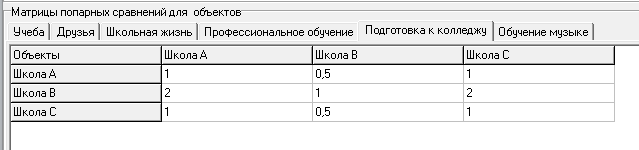
M5		Школа A	Школа B	Школа C
	Школа A	1	0,5	1
	Школа B	2	1	2
	Школа C	2	0,5	1
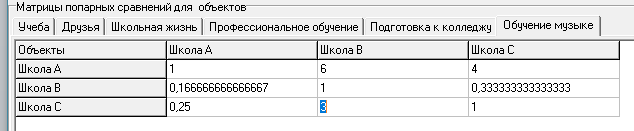
M6		Школа A	Школа B	Школа C
	Школа A	1	6	4
	Школа B	0,166666667	1	0,333333333
	Школа C	0,25	3	1

Компонента собственного вектора:

n-характеристика	Результат
1	3,464101615
2	1,012272234
3	0,133481894
4	0,863340021
5	2,236067977
6	1,10668192

Нормализация компоненты собственного вектора:

n-характеристика	До нормализации	После нормализации,a
1	3,464101615	0,216506351
2	1,012272234	0,081307007
3	0,133481894	0,065340787
4	0,863340021	0,099616156
5	2,236067977	0,14583052
6	1,10668192	0,095540885

Оценка вектора приоритета характеристик:

n-характеристика	Норм. Компонента собственного вектора	Оценка вектора
1	0,216506351	1,657027998
2	0,081307007	1,016374565
3	0,065340787	0,214137674
4	0,099616156	0,847606262
5	0,14583052	1,337477087
6	0,095540885	0,970477847

Оценка вектора приоритета для объектов:

M1	Школа A	Школа B	Школа C	НеНорм. Компонента собственного вектора	Норм. Компонента собственного вектора	Оценка вектора
Школа A	1	0,333333333	0,5	0,638943104	0,34851442	0,566533
Школа B	3	1	3	1,732050808	0,24743583	2,106221
Школа C	2	0,333333333	1	0,903602004	0,271080601	1,050588
M2	Школа A	Школа B	Школа C	НеНорм. Компонента собственного вектора	Норм. Компонента собственного вектора	Оценка вектора
Школа A	1	1	1	1	0,333333333	1
Школа B	1	1	1	1	0,333333333	1
Школа C	1	1	1	1	0,333333333	1
M3	Школа A	Школа B	Школа C	НеНорм. Компонента собственного вектора	Норм. Компонента собственного вектора	Оценка вектора
Школа A	1	5	1	1,495348781	0,213621254	2,033098
Школа B	0,2	1	0,2	0,447213595	0,319438282	0,40662
Школа C	2	5	1	1,77827941	0,222284926	2,246719
M4	Школа A	Школа B	Школа C	НеНорм. Компонента собственного вектора	Норм. Компонента собственного вектора	Оценка вектора
Школа A	1	9	7	2,817313247	0,165724309	3,863654
Школа B	0,111111111	1	0,2	0,386097395	0,294481064	0,342826
Школа C	0,142857143	5	1	0,919322715	0,149657186	1,645737
M5	Школа A	Школа B	Школа C	НеНорм. Компонента собственного вектора	Норм. Компонента собственного вектора	Оценка вектора
Школа A	1	0,5	1	0,840896415	0,336358566	0,763494
Школа B	2	1	2	1,414213562	0,282842712	1,526988
Школа C	2	0,5	1	1	0,285714286	1,099853
M6	Школа A	Школа B	Школа C	НеНорм. Компонента собственного вектора	Норм. Компонента собственного вектора	Оценка вектора
Школа A	1	6	4	2,213363839	0,201214894	3,019045
Школа B	0,166666667	1	0,333333333	0,485491772	0,323661181	0,430186
Школа C	0,25	3	1	0,930604859	0,218965849	1,240253

Оценка обобщенного приоритета:

Объект	M1	M2	M3	M4	M5	M6	Оценка обобщенного приоритета
Школа A	0,566533331	1	2,033097593	3,863654189	0,763494208	3,019045	0,833032406
Школа B	2,106220894	1	0,406619519	0,342826313	1,526988416	0,430186	0,820718601
Школа C	1,050588052	1	2,246718848	1,645737408	1,099852774	1,240253	0,779902508

Результат:

Школа А является наиболее выгодным решением, т.к. в процессе анализа был получен наибольший результат.