Отчет о выполнении работы по дисциплине методы оптимизации Тема: Метод дихотомии. Метод дихотомии
 Скачать 176.7 Kb. Скачать 176.7 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования ОТЧЁТ О ВЫПОЛНЕНИИ РАБОТЫ по дисциплине методы оптимизации Тема: Метод дихотомии. Работу выполнил _________________________________ студент (подпись) Работу проверил _________________________________ Преподаватель (подпись) 2022 1 Постановка задачи Требуется найти безусловный минимум функции: 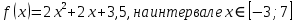 с точностью δ = 0.2 с помощью метода дихотомии. с точностью δ = 0.2 с помощью метода дихотомии.2 Стратегия поиска Метод относится к последовательным стратегиям. Задается начальный интервал неопределенности и требуемая точность. Алгоритм опирается на анализ значений функции в двух точках. Для их нахождения текущий интервал неопределенности делится пополам и в обе стороны от середины откладывается по 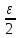 , где , где 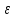 - малое положительное число. Условия окончания процесса поиска стандартные: поиск заканчивается, когда длина текущего интервала неопределенности оказывается меньше установленной величины. - малое положительное число. Условия окончания процесса поиска стандартные: поиск заканчивается, когда длина текущего интервала неопределенности оказывается меньше установленной величины.3 Алгоритм Шаг 1. Задать начальный интервал неопределенности 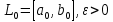 – малое число, l > 0 – точность. – малое число, l > 0 – точность.Шаг 2. Положить k = 0. Шаг 3. Вычислить 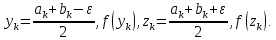 Шаг 4. Сравнить 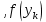 c c 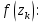 a) если 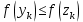 , положить , положить 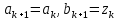 (рис. 1) и перейти к шагу 5; (рис. 1) и перейти к шагу 5;b) если 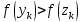 , положить , положить 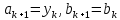 (рис. 1); (рис. 1);Шаг 5. Вычислить 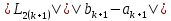 и проверить условие окончания: и проверить условие окончания:a) если 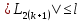 , процесс поиска завершается и , процесс поиска завершается и 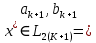 ]. В качестве приближенного решения можно взять середину последнего интервала: ]. В качестве приближенного решения можно взять середину последнего интервала: 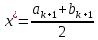 ; ;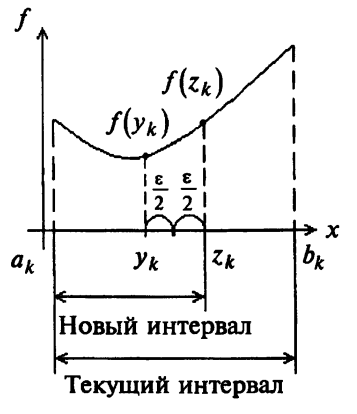 Рисунок 1. b) если 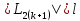 , положить , положить 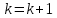 и перейти к шагу 3. и перейти к шагу 3.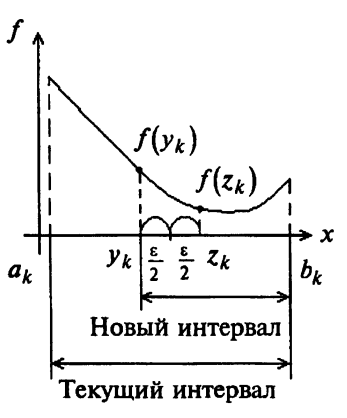 Рисунок 2. 4 Программная реализация На рисунках 3-5 предоставлена реализация метода дихотомии на программном языке С#. 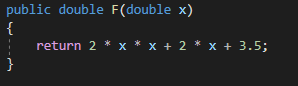 Рисунок 3. 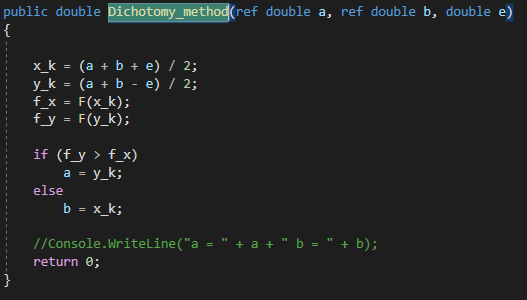 Рисунок 4. 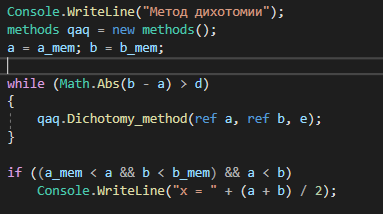 Рисунок 5. На рисунках 3 и 4 изображены функции класса method реализующие вычисление исходной функции (рисунок 3) и 3 и 4 шаги алгоритма поиска нуля функции (рисунок 4). На рисунке 5 изображены цикл 3 и 4 шагов, а также проверка условия выхода из этого цикла – 5 шаг. 5. Сходимость Для метода дихотомии характеристика относительного уменьшения начального интервала неопределенности находится по формуле 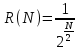 , где N – количество вычислений функции. , где N – количество вычислений функции.R(6) 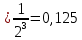 6. Результаты вычислений Результаты вычислений приведены на рисунке 7. Где: a и b – границы промежутка yk и zk – значения y и z на текущей итерации F(y) и F(z) -значение функции на текущей итерации x – искомый минимум 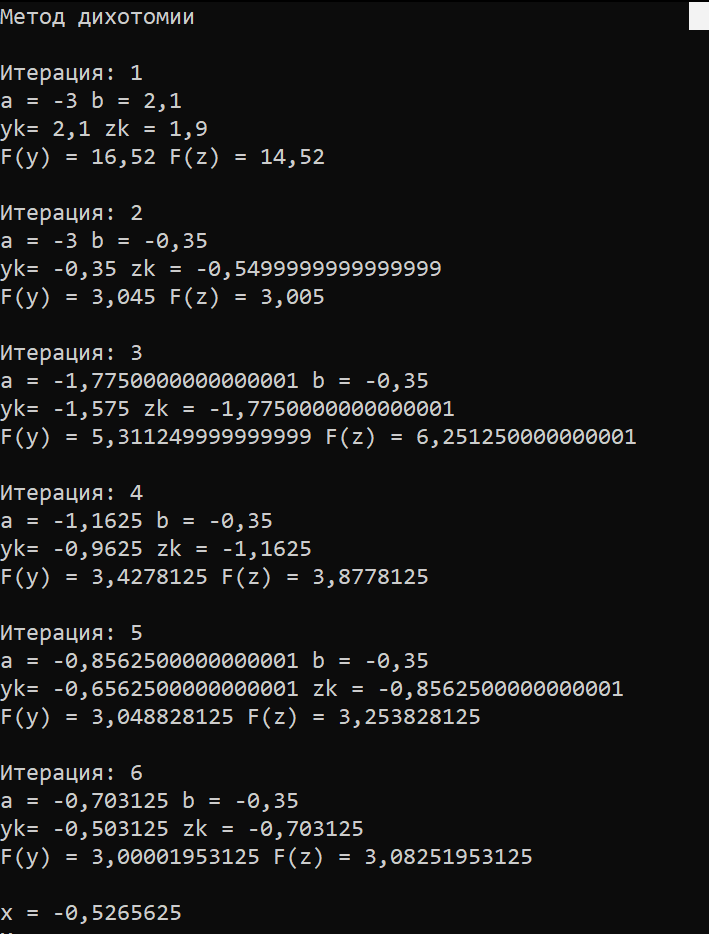 Рисунок 7. Список литературы 1. Методы оптимизации в примерах и задачах Пантелеев А.В_2005 -544с |
