Метод Фибоначи. Метод Фибоначчи
 Скачать 359.47 Kb. Скачать 359.47 Kb.
|
|
Метод Фибоначчи. Часто в вычислительных процедурах существенные трудности возникают в связи с вычислениями значений 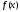 . Например, . Например, 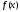 вычисляется в процессе эксперимента, либо вычисляется в процессе эксперимента, либо 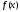 задана сложной формулой. задана сложной формулой.К методам, в которых при ограничениях на количество вычислений значений 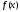 достигается в определенном смысле наилучшая точность, относятся методы Фибоначчи и золотого сечения. достигается в определенном смысле наилучшая точность, относятся методы Фибоначчи и золотого сечения.Как и в методе дихотомии, процедура будет заключаться в последовательном уменьшении отрезка неопределенности на основании анализа значений функции в двух внутренних точках отрезка с существенным отличием от предыдущего, состоящего в том, что одна из внутренних точек последующего отрезка неопределенности совпадет с одной из двух внутренних точек предыдущего отрезка неопределенности. Определение. Последовательность чисел 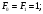 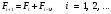 называется последовательностью Фибоначчи. называется последовательностью Фибоначчи.Зададимся некоторым 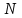 и выпишем последовательность чисел Фибоначчи. и выпишем последовательность чисел Фибоначчи.Итак, необходимо найти минимум 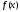 на отрезке на отрезке 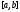 с точностью с точностью  . .Опишем 1-й шаг метода Фибоначчи. Как и в предыдущем методе найдем 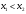 на отрезке на отрезке 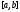 : :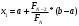 ; ; 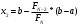 Из формул видно, что 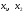 симметричны относительно середины отрезка симметричны относительно середины отрезка 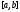 . .Дальнейшая процедура уменьшения отрезка неопределенности совпадает с методом дихотомии. Итак, основное отличие метода Фибоначчи от метода дихотомии состоит в выборе точек 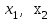 на каждом шаге. на каждом шаге.В силу свойств последовательности Фибоначчи, на каждом шаге, кроме 1-го и предпоследнего, вычисляется одно новое значение функции, другое значение используется из предыдущего шага. Только на 1-м шаге значение 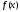 вычисляется дважды, а на предпоследнем, когда вычисляется дважды, а на предпоследнем, когда 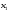 совпадает с совпадает с 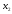 , , 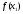 известно из предыдущего шага. Можно показать, что на известно из предыдущего шага. Можно показать, что на 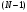 -м шаге -м шаге 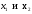 совпадут, этим завершится процедура деления отрезка неопределенности. Для получения окончательного результата необходимо вычислить совпадут, этим завершится процедура деления отрезка неопределенности. Для получения окончательного результата необходимо вычислить 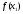 и и 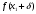 , где , где 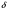 - малая величина, параметр метода. - малая величина, параметр метода.Если 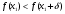 , то полагают, что , то полагают, что 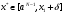 , в противном случае , в противном случае 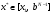 . .Посмотрим, как уменьшается отрезок неопределенности 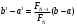 ; ;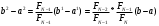 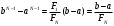 Таким образом, 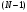 -й шаг метода Фибоначчи обеспечивает уменьшение длины отрезка неопределенности в -й шаг метода Фибоначчи обеспечивает уменьшение длины отрезка неопределенности в 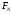 раз. раз.Для решения задачи минимизации с заданной точностью  необходимо решить неравенство необходимо решить неравенство 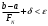 относительно относительно 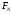 , получить последовательность чисел Фибоначчи , получить последовательность чисел Фибоначчи 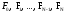 и использовать ее с конца. и использовать ее с конца.Замечание 1. Теоретически достаточно найти первую точку метода 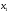 , остальные точки можно получать, используя свойство их симметрии относительно центра отрезка, однако в этом случае быстро накапливается погрешность. Чтобы избежать накопления погрешности, следует пересчитывать точки , остальные точки можно получать, используя свойство их симметрии относительно центра отрезка, однако в этом случае быстро накапливается погрешность. Чтобы избежать накопления погрешности, следует пересчитывать точки 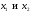 по соответствующим формулам. по соответствующим формулам.Замечание 2. Поскольку 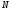 определяется сначала как функция от определяется сначала как функция от  , алгоритм не позволяет получить более точный результат путем продолжения счета. Для обеспечения другой точности необходимо реализовать новую вычислительную процедуру. , алгоритм не позволяет получить более точный результат путем продолжения счета. Для обеспечения другой точности необходимо реализовать новую вычислительную процедуру.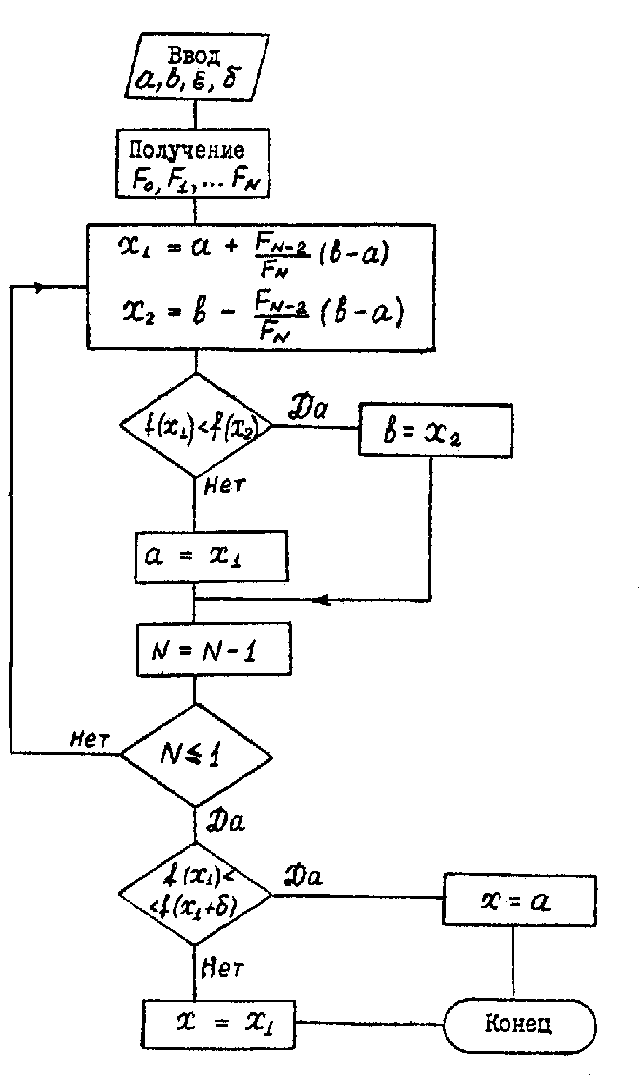 Блок-схема метода Фибоначчи Пример. Найти минимум 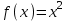 на отрезке на отрезке 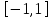 c c 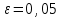 . Начнем с определения . Начнем с определения 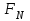 : :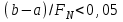 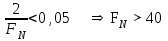 Для решения поставленной задачи потребуется 9 шагов по методу Фибоначчи, при этом понадобится 9 раз вычислять 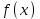 . Заметим, что для решения этой же задачи методом дихотомии мы проделали 7 шагов, то есть . Заметим, что для решения этой же задачи методом дихотомии мы проделали 7 шагов, то есть 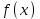 вычисляли 14 раз. вычисляли 14 раз.1-й шаг. 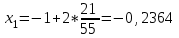 ; ; 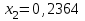 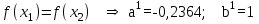 . .2-й шаг. 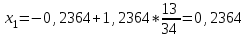 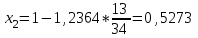 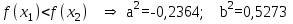 . .3-й шаг. 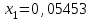 ; ; 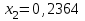 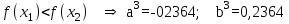 . .4-й шаг. 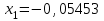 ; ; 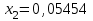 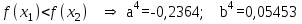 . .5-й шаг. 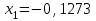 ; ; 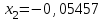 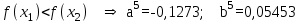 . .6-й шаг. 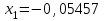 ; ; 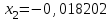 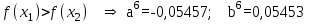 . .7-й шаг. 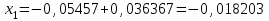 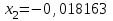 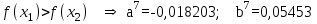 . .8-й шаг. 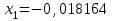 ; ; 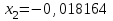 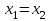 . .9-й шаг. 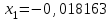 ; ; 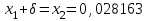 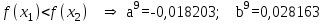 . .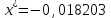 Замечание. Вычисления проводились с 5 знаками после запятой, поэтому точки последующего и предыдущего шага совпадают не полностью. Метод золотого сечения. В теории чисел показано, что существует предел отношения соседних чисел Фибоначчи 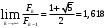 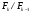 показывает, как соотносятся длины отрезков неопределенности при применении метода Фибоначчи. показывает, как соотносятся длины отрезков неопределенности при применении метода Фибоначчи.С другой стороны, рассмотрим следующую задачу. Возьмем отрезок 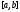 , найдем внутри этого отрезка , найдем внутри этого отрезка 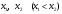 , образующие золотое сечение. , образующие золотое сечение.Для этого необходимо выполнение следующих условий: 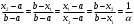 Найдем  ,при котором возможны равенства ,при котором возможны равенства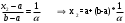 , ,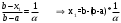 , ,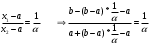 , , 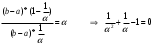 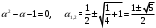 Поскольку 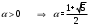 Отсюда видно, что золотое сечение можно рассматривать как предельный случай деления отрезка по методу Фибоначчи при большом k. Метод золотого сечения состоит в том, что начиная с 1-го шага отрезок делится точками 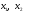 в пропорции золотого сечения. При каждом шаге отрезок неопределенности уменьшается в в пропорции золотого сечения. При каждом шаге отрезок неопределенности уменьшается в  раз. раз.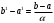 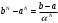 Если  - заданная точность, то число шагов метода золотого сечения следует находить как решение неравенства - заданная точность, то число шагов метода золотого сечения следует находить как решение неравенства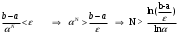 Замечание. Метод золотого сечения немного медленнее сходится, чем метод Фибоначчи. С другой стороны, при необходимости, для получения более точного результата, есть возможность его продолжить. При 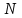 шагах метода золотого сечения шагах метода золотого сечения 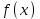 вычисляется вычисляется 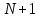 раз, так как на 1-м шаге раз, так как на 1-м шаге 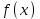 вычисляется дважды, а на последующих шагах по одному разу, так же как и в методе Фибоначчи одна из внутренних точек отрезка неопределенности последующего шага совпадает с одной из точек предыдущего шага. вычисляется дважды, а на последующих шагах по одному разу, так же как и в методе Фибоначчи одна из внутренних точек отрезка неопределенности последующего шага совпадает с одной из точек предыдущего шага.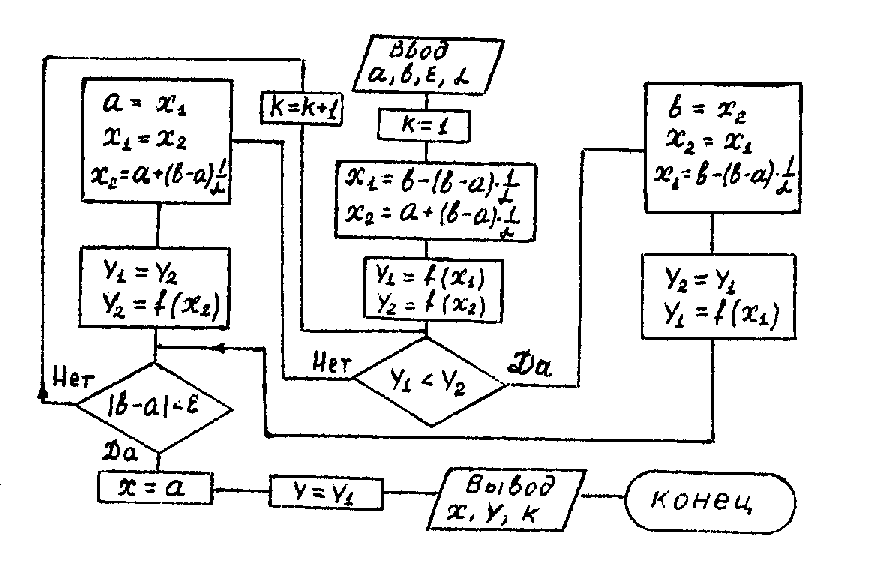 Блок-схема метода золотого сечения Пример. Найти минимум 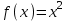 на отрезке на отрезке 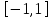 c c 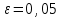 Предварительно определим, сколько потребуется шагов метода золотого сечения. 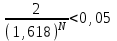 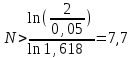 Итак, потребуется 8 шагов метода золотого сечения, при этом значения 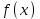 придется вычислять 9 раз, то есть трудоемкость такая же, как была в методе Фибоначчи. придется вычислять 9 раз, то есть трудоемкость такая же, как была в методе Фибоначчи.1-й шаг. 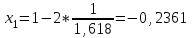 ; ;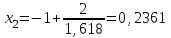 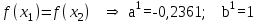 . .2-й шаг. 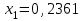 ; ;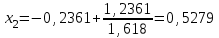 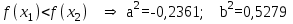 . .3-й шаг. 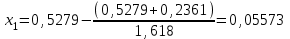 ; ;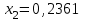 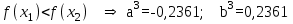 . .4-й шаг. 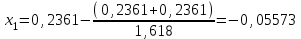 ; ;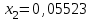 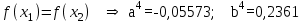 . .5-й шаг. 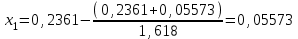 ; ;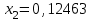 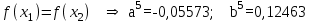 . .6-й шаг. 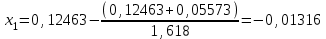 ; ;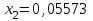 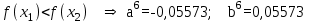 . .7-й шаг. 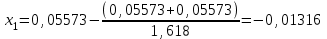 ; ;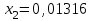 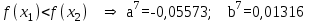 . .8-й шаг. 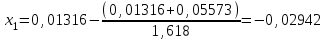 ; ;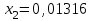 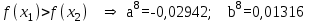 . . Метод Фибоначчи используется для нахождения безусловного минимума унимодальных функций f(x). Функция f(x) называется унимодальной на отрезке [a,b], если
Свойства унимодальных функций. Пусть f(x) унимодальна на [a,b], x,z принадлежат отрезку, x 1) если f(x) 2) если f(x)>f(z), то x* принадлежит [x,b]; 3) если f(x)=f(z), то x* принадлежит [x,z]; Алгоритм. 1) Задаются: отрезок локализации L0 = [a0,b0], ε > 0, l > 0, (отрезок локализации можно найти алгоритмом Свена); 2) Необходимо найти N – количество вычислений как наименьшее целое число, при котором FN >= | L0 | / l 3) Количество итераций k = 0; 4) Вычисляются: xk=ak + (FN-2 / FN) * (bk - ak) yk=ak + (FN-1 / FN) * (bk - ak) 5) Вычисляютсяи сравниваются f(xk) и f(yk) 5.1) если f(xk) <= f(yk) , то ak+1 = ak bk+1 = yk yk +1 = xk xk+1= ak+1 + (FN – k — 3 / FN — k — 1) * (bk - ak) 5.2) если f(xk) > f(yk) , то ak+1 = xk bk+1 = bk xk+1=yk yk+1= ak+1 + (FN – k — 2 / FN — k — 1) * (bk - ak) 6) если k ≠ N-3, то k=k+1 и к 5) если k= N-3, то xN-2=yN-2 = (aN – 2 + bN – 2)/2 xN-1 = xN-2 = yN-2 yN-1= xN-1+ ε 7) в xN-1 и yN-1 вычисляются значения функции и находятся границы конечного отрезка локализации 7.1) если f(xN-1) <= f(yN -1), то aN — 1 = aN — 2 bN — 2 = yN — 1 7.2) если f(xN-1) > f(yN -1), то aN — 2 = xN — 1 bN — 1 = bN — 2 8) x*=(ak+1 + bk+1)/2 Найдем минимум функции: f(x) = (x-3)2 Используем для этого Метод Фибоначчи. Важнейшая особенность этого метода состоит в том, что он позволяет для заранее заданного числа вычислений функции построить оптимальную процедуру поиска минимума унимодальной функции. Предположим, что заданный начальный интервал неопределенности [a1,b1], [ai,bi] является интервалом неопределенности, полученным на i-той итерации. Рассмотрим две точки λi и μi из интервала [ai,bi], заданные с помощью соотношений: где n - заданное число вычислений функции; Fk - последовательность чисел Фибоначчи, заданная с помощью рекуррентной формулы: Fk+1 = Fk + Fk-1, k = 1,2, … , где F0 = F1 = 1 Новый интервал неопределенности (ai+1,bi+1) равен (λi,bi), если f(λi) > f(μi), и равен (ai, μi), если f(λi) < f(μi). Тогда в первом случае, новый интервал неопределенности имеет длину: Отсюда следует, что в любом случае на i-той итерации интервал неопределенности сжимается в Fn-i/Fn-i+1 раз. На (i+1)-ой итерации либо λi+1 = μi, либо μi+1 = λi. Поэтому на каждом шаге вычисляется только одно новое значение функции. На (n-1)-ой итерации λn-1 = μn-1,и значение функции не вычисляется. Если ε есть точность вычисления значения функции, n – максимально возможное число вычислений функции, то конечный интервал неопределенности будет равен: Решение. Последовательность чисел Фибоначчи имеет вид: 1,1,2,3,5,8,13,21,34,55,89,144, Итерация 1. Вычислим точки f(λ1) = 3.4371; f(μ1) = 1.3135 Так как f(λ1) > f(μ1), то сокращаем интервал неопределенности и принимаем на второй итерации: a2 = λ1 = 1.1460674157303; b2 = b1 = 3 Итерация 2. Вычислим точки f(λ2) = 1.3135; f(μ2) = 0.5011 Так как f(λ2) > f(μ2), то сокращаем интервал неопределенности и принимаем на 3-й итерации: a3 = λ2 = 1.8539325842697; b3 = b2 = 3 Итерация 3. Вычислим точки f(λ3) = 0.5011; f(μ3) = 0.192 Так как f(λ3) > f(μ3), то сокращаем интервал неопределенности и принимаем на 4-й итерации: a4 = λ3 = 2.2921348314607; b4 = b3 = 3 Итерация 4. Вычислим точки f(λ4) = 0.192; f(μ4) = 0.07272 Так как f(λ4) > f(μ4), то сокращаем интервал неопределенности и принимаем на 5-й итерации: a5 = λ4 = 2.561797752809; b5 = b4 = 3 Все вычисления сведены в таблицу. Вычисления продолжаются, пока не найдены 10 новых точек.
Вычисляем точку минимума функции f(xmin) = 0.00114 Ответ: x = 2.9663; F(x) = 0.00114 Количество итераций, N = 8
|
