Расширение полей 4 Глава Поле алгебраических чисел 9 1 Алгебраические числа основные понятия 9
 Скачать 107.67 Kb. Скачать 107.67 Kb.
|
ОглавлениеВведение 2 Глава 1. Расширение полей 4 Глава 2. Поле алгебраических чисел 9 2.1 Алгебраические числа: основные понятия 9 2.2 Поле алгебраических чисел 13 Заключение 26 Список использованных источников 27 Введение Теория чисел - раздел математики, занимающийся изучением свойств чисел как математических объектов. Теория чисел возникла как продолжение арифметики, то есть, науки о натуральных числах. На протяжении многих столетий понятие числа углублялось и пополнялось новыми элементами. В настоящее время в теорию чисел включают изучение не только натуральных чисел, но и множества целых чисел, множества рациональных чисел, множества алгебраических чисел а также изучение функций различного происхождения, которые связаны с арифметикой целых чисел и их обобщений. Если рассматривать многочлен:  с целыми коэффициентами, то целые числа являются корнями многочлена, когда этот многочлен имеет степень n=1. Тогда, во множестве комплексных чисел естественно выделить целые алгебраические числа, представляющие собой корни многочленов с целыми коэффициентами. с целыми коэффициентами, то целые числа являются корнями многочлена, когда этот многочлен имеет степень n=1. Тогда, во множестве комплексных чисел естественно выделить целые алгебраические числа, представляющие собой корни многочленов с целыми коэффициентами.Изучение свойств таких чисел - задача алгебраической теорией чисел. Она занимается изучением различных классов алгебраических чисел. Мир чисел и по наши дни таит в себе много загадок и нерешенных вопросов и притягивает к себе многие выдающиеся умы. Целью настоящей работы является не только показать современное состояние теории алгебраических чисел и зложить основные методы этой теории, но и дать представление об историческом ходе развития ее методов и о тех связях, которые существуют между этой теорией и другими проблемами теории чисел. Глава 1. Расширение полей Пусть P[x] — кольцо полиномов от x над полем P, где P — подполе поля F. Напомним, что элемент a поля F называется алгебраическим над полем P, если a является корнем какого-нибудь полинома положительной степени из P [x]. Определение. Пусть P < F и a0F. Простым расширением поля P с помощью элемента a называется наименьшее подполе поля F, содержащее множество Р и элемент a. Простое расширение P с помощью a обозначается через P (a), основное множество поля P (a) обозначается через Р(a)[3]. Пусть a0F, P [x] — кольцо полиномов от x и  т. е. P [a] есть множество всех выражений вида  где а0, a1,...an0P и n — любое натуральное число. Легко видеть, что алгебра +P[a], +, —, ., 1, — подкольцо поля P (a) — является кольцом; это кольцо обозначается символом P [a]. Теорема 1.1. Пусть P [x]— кольцо полиномов от х над P и P (a)— простое расширение поля P. Пусть y — отображение P[x] на P[a] такое, что y(f)=f(a) для любого f из P[x]. Тогда: (а) для любого а из Р y (а) = а; (b) y(x) = a; (с) y является гомоморфизмом кольца P [x] на кольцо P [a]; (d)  y y(е) фактор-кольцо P [x]/Кег y изоморфно кольцу P [a]. Доказательство. Утверждения (а) и (Ь) непосредственно следуют из определения y. Отображение y сохраняет главные операции кольца P [x], так как для любых f и g из P[x] 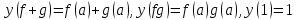 Далее, по условию, y есть отображение Р[х] на Р[a]. Следовательно, y является гомоморфизмом кольца P [x] на кольцо P [a]. Утверждение (d) непосредственно следует из определения отображения y[10]. Поскольку y — гомоморфизм кольца P [x] на P [a], то фактор-кольцо P[x]/Кег y изоморфно кольцу P [a]. Следствие 1.2. Пусть a — трансцендентный элемент над полем P. Тогда кольцо полиномов P [x] изоморфно кольцу P [a]. Доказательство. В силу трансцендентности a над P Kery={0}. Поэтому P[x]/{0}– P [a]. Кроме того, фактор-кольцо кольца P [x] по нулевому идеалу изоморфно P [x]. Следовательно, P [x]– P [a]. Пример 4.1[5,с.159]. Пусть F = Q(a) и а является корнем многочлена  .Найдите минимальный многочлен элемента .Найдите минимальный многочлен элемента 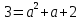 Решение. По условию,  , отсюда , отсюда 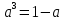 . Из данного по условию равенства . Из данного по условию равенства  находим находим 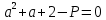 . Умножив данное равенство на а, получаем . Умножив данное равенство на а, получаем  , откуда , откуда  Наконец,  , откуда , откуда  . Таким образом, приходим к системе равенств . Таким образом, приходим к системе равенств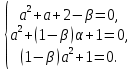 Исключая а2 и а, приходим к равенству  , которое говорит о том, что Р является корнем многочлена , которое говорит о том, что Р является корнем многочлена  . Этот многочлен, как легко видеть, не имеет рационль- ных корней, а значит, неприводим над полем Q. Следовательно, ф(х) является искомым минимальным многочленом алгебраического над полем Q элемента р[15,с.11]. . Этот многочлен, как легко видеть, не имеет рационль- ных корней, а значит, неприводим над полем Q. Следовательно, ф(х) является искомым минимальным многочленом алгебраического над полем Q элемента р[15,с.11].Заметим, что при исключении а из системы равенств можно привлечь знания по решению систем линейных уравнений. Равенства системы говорят о том, что вектор (а2, а, 1) является ненулевым решением однородной системы линейных уравнений  Следовательно, определитель матрицы системы равен нулю:  Отсюда получаем равенство  . .Наконец, отметим, что это упражнение можно превратить в школьную задачу: известно, что  ; найдите уравнение с целыми коэффициентами, корнем которого является р. ; найдите уравнение с целыми коэффициентами, корнем которого является р.До сих пор мы присоединяли лишь по одному элементу. Перейдем к естественному обобщению простого расширения поля. Определение 4.10. Пусть поле F является расширением поля Р и а1; а2, ..., ап е F. Составным расширением поля Р с помощью присоединения элементов М = {а1; а2, ..., а,,} называется поле, которое получается из элементов поля Р и элементов множества М с помощью операций сложения, вычитания, умножения и деления. Обозначение: Р(аь а2,..., а„). Если присоединяемые элементы алгебраические, то говорят о составном алгебраическом расширении поля. Теорема 4.7. Составное алгебраическое расширение поля можно получить с помощью ряда повторных расширений[11,с.12]. Доказательство. Пусть ах, а2, ..., ап — алгебраические элементы над полем Р. Докажем, что Р(аь а2, ..., а„) = P(aj)(a2)... (а„). Поскольку с Р(а1)(а2)...(ап), аа, а2, ..., ап е Р(а1)(а2)... («„), то Р(а1; а2,..., а„) с Р(ах)(а2)...(а„). Обратное включение докажем индукцией по п. При п = 1 утверждение очевидно. Пусть уже доказано, что Рх = Р(аД (а2)... с Р(ах, а2, ..., ап_х), докажем, что Р2 = P(aj)(a2)... (a„) с P(aa, a2, ..., ап). По теореме о строении простого алгебраического расширения, всякий элемент Ре Р2 = Рх (а„) является линейной комбинацией степеней элемента а„ с коэффициентами из поля F1. По индуктивному предположению, Рх с Р(аь а2,..., а„_х) с Р(аь а2,..., ос,,_г, а„). Следовательно, Р2 = F1(an) с с Р(аь а2,..., аГ!). Таким образом, Р(аь а2,..., a„) =P(a1)(a2)... (a„). Теорема доказана. Рассмотрим составные расширения числовых полей. Начнем с примера. Пример 4.2[12,с.124]. Докажем, что составное алгебраическое расширение Q(f2, /з) можно получить присоединением к Q одного элемента 42 + 4з. В самом деле, числа 42и4з можно получить в виде линейных комбинаций степеней 1 = а0, а, а2, а3. (Докажите!) Следовательно, <0>(л/2,4з) с Q(V2 + 4з). Обратное включение очевидно. Элемент а в этом случае называется примитивным. Докажем существование такого элемента в значительно более общей ситуации. Теорема 4.8 (о примитивном элементе). Составное алгебраическое расширение числового поля является простым[6,с.112]. Доказательство. Пусть Р — числовое поле. Докажем, что составное алгебраическое расширение F = Р(a, Р) является простым, т.е. существует примитивный элемент 0 е F, такой что Р(а, Р) = Р(0). Пусть Дх) и g(x) — минимальные многочлены элементов соответственно а и Р над полем Р. Пусть otj = а, а2, ..., ак — все различные корни многочлена Дх) и Рх = Р, р2, ..., Рт — все различные корни многочлена g(x). Рассмотрим уравнения а; + хР; = а + хР для всех 1 < i < к и 1 < j < т. Предположим, что одно из этих уравнений имеет два различных корня Cj и с2. Тогда а; + CjPj = а + схР и а, + с2Р; = а + с2р. Вычитая из первого равенства второе, получим (cj - с2)Р; = (сх - с2)Р, откуда Р, = Р = Рх, что противоречит условию. Следовательно, каждое из рассматриваемых уравнений имеет в Р не более одного решения. Поскольку поле Р бесконечно, то существует элемент с е Р, который не является корнем ни одного из данных уравнений. Обозначим 0 = а + сР и докажем, что Р(а, Р) = Р(0). Очевидно, Р(а, Р) з Р(0). Следовательно, существует номер i, такой что а, = 0 - ср;, откуда а + сР = 0 = а,- + сР;. Если предположить, что Р( Ф Р, то приходим к противоречию с выбором элемента с. Следовательно, Р- = Р и Р оказывается кратным корнем многочлена F. Но этот многочлен неприводим над полем Р, а значит, взаимно прост со своей производной и не может иметь кратных корней. Таким образом, НОД((х),/(0 - сР)) = х - р. Алгоритм Евклида для нахождения НОД двух многочленов показывает, что коэффициенты многочлена, являющегося НОД, принадлежат тому же полю, что и коэффициенты многочленов g(x) и/(0 - сх), т.е. полю Р(в). Следовательно, р е Р(0). Но тогда а е Р(0). Таким образом, доказано включение Р(а, Р) с Р(0), а вместе с тем и равенство Р(а, Р) = Р(0). Пусть теперь дано составное алгебраическое расширение F числового поля Р. Тогда F = Р(а, Р, у, ..., S) и, по доказанному, Р(а, р, у,..., 8) = Р(а, р)(у,..., 8) = P(0j)(y,..., 8) = ... = Р(0„). Глава 2. Поле алгебраических чисел 2.1 Алгебраические числа: основные понятия С точки зрения важного для алгебры понятия алгебраического уравнения, естественным представляется выделение классов чисел, которые являются корнями алгебраических уравнений, с коэффициентами из некоторого определенного множества чисел[13,с.23]. Определение 1 [1, стр. 259]: Комплексное или действительное число z называется алгебраическим, если оно является корнем какого-нибудь алгебраического уравнения с целыми коэффициентами: anxn+an-1xn-1+ … +a1x+a0=0 (a0, a1, …, anZ; an0). Для определения алгебраического числа можно рассматривать многочлены с рациональными коэффициентами, поскольку, приведением к общему знаменателю и умножением всего уравнения на этот общий знаменатель такое уравнение с помощью элементарных преобразований можно привести к уравнению с целыми коэффициентами, корнем которого будет наше число. К алгебраическим числам принадлежат, в частности, и все рациональные числа. Действительно, рациональное число z= (p, qN) очевидно является корнем уравнения: qx-p=0[9,с.10].  Также всякое значение корня любой степени из рационального числа является алгебраическим числом. Действительно, число z= (p, qN) является корнем уравнения: qxn-p=0. Существуют алгебраические числа и иного вида, нежели указанное выше. Пример:  Чиcло z= является алгебраическим. Действительно, возводя в квадрат обе части равенства, определяющего число z, получим: z2=2+2+3. Отсюда z2-5=. Возводя в квадрат обе части этого равенства, получим: z4-10z2+25=24. Отсюда следует, что число z является корнем следующего уравнения: x4-10x2+1=0.  Чиcло z= тоже является алгебраическим. Действительно, возведем в куб обе части равенства , получим: . Запишем это равенство в следующем виде: и возведем обе части полученного равенства в квадрат. После соответствующих преобразований получим уравнение, корнем которого является число z=:  Всякое число z=a+bi, у которого компоненты a и b - рациональные числа, являются алгебраическими. Докажем это.  Из равенства , получаем: . Отсюда, возводя в квадрат, получим: . Следовательно, z является корнем уравнения с целыми коэффициентами:  Например, найдем уравнение, корнем которого является комплексное число . Исходя из вышесказанного данное комплексное число является корнем уравнения , что проверяется подстановкой: 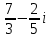  В дальнейшем мы будем рассматривать только действительные алгебраические числа, не оговаривая этого каждый раз[7,с.41]. Определение 2: Число n называется степенью алгебраического числа z, если z является корнем многочлена n-ой степени с рациональными коэффициентами и не является корнем тождественно не равного нулю многочлена с рациональными коэффициентами степени, меньшей чем n. Рациональные числа являются алгебраическими числами первой степени. Любая квадратическая иррациональность представляет собой алгебраическое число 2-й степени. Алгебраические числа 3-й степени часто называют кубическими иррациональностями, а 4-й степени биквадратическими иррациональностями[14,с.10]. Пример: - алгебраическое число 3-й степени, т.е. кубическая иррациональность, поскольку, это число является корнем многочлена 3-й степени с целыми коэффициентами x3-2=0 и не является корнем какого-либо многочлена 1-й или 2-й степени с целыми коэффициентами. Определение 3 [1, стр. 260]: Если алгебраическое число n-й степени z является корнем многочлена f(x)=xn+b1xn-1+ … +bn (n1) (1) с рациональными коэффициентами, то f(x) называется минимальным многочленом для z. Заметим, что старший коэффициент этого многочлена равен 1. Пример: Минимальным многочленом для является x3-2, так как корень этого многочлена не является корнем какого-либо многочлена степени, меньшей, чем 3 с рациональными коэффициентами. Определение 4 [4, стр. 520]. Неприводимый многочлен - это многочлен, не разлагающийся на множители более низкой степени, отличной от нуля. Если многочлен разлагается на множители более низкой степени, отличной от нуля, то, соответственно, такой многочлен есть приводимым многочленом. Теорема 1 [1, стр. 261]: Если f(x) минимальный многочлен алгебраического числа z и F(x) многочлен с рациональными коэффициентами, такой, что F(z)=0, то f(x) делитель F(x), т.е. F(x)=f(x) g(x), где g(x) также многочлен с рациональными коэффициентами[7,с.260]. Доказательство: Согласно известной теореме алгебры о делении с остачей F(x) можно представить в виде: F(x)=f(x) g(x)+r(x) где g(x) и r(x) - многочлены с рациональными коэффициентами, причем степень r(x) меньше степени f(x). Поскольку F(z)=0 и f(z)=0, то придавая x значение z, получаем r(z)=0; z - корень многочлена r(x) с рациональными коэффициентами степени, меньшей чем у минимального для z многочлена, т.е. меньшей чем степень z. Это может быть только если r(x) тождественно равен нулю, а значит F(x)=f(x) g(x). Теорема доказана. Теорема 2 [1, стр. 261]: Для любого алгебраического числа z минимальный многочлен неприводим над полем рациональных чисел. Доказательство: Пусть f(x) - минимальный многочлен для z. Предположим, что f(x) приводим над полем рациональных чисел, т.е., что f(x)=(x)(x), (x)(x) - многочлены с рациональными коэффициентами, степени меньшей, чем n. Из равенства (x)(x)=f(x)=0 следует, что из двух чисел (x) и (x), по крайней мере одно равно нулю. Пусть например (x)=0, тогда z - корень тождественно не равного нулю многочлена (x) с рациональными коэффициентами, степени меньшей, чем n, т.е. меньшей чем у f(x). А это противоречит тому, что f(x) - минимальный многочлен для z. Предположение, что f(x) приводим над полем рациональных чисел, оказалось неверным, т.е. f(x) неприводим над этим полем. Теорема доказана. Теорема 3 [1, стр. 261]: Если z корень неприводимого над полем рациональных чисел многочлена F(x) с рациональными коэффициентами степени n, то z - алгебраическое число степени n. Доказательство: Обозначим минимальный многочлен для z через f(x). Согласно теоремы 1: F(x)=f(x) g(x); где g(x) - многочлен с рациональными коэффициентами. Поскольку F(x) неприводим над полем рациональных чисел и f(x) отлично от постоянного, то g(x)=c, где c - рационально. F(x)=cf(x), т.е. z - алгебраическое число n-й степени. Теорема доказана[3,с. 109]. Пример: Пусть p - простое число. при любом простом целом a (a>1), не равном p-ой степени другого целого, представляет собой алгебраическое число степени p. Действительно это число есть корень неприводимого над полем рациональных чисел многочлена. xp-a=0 Если z - алгебраическое число степени n и f(x) - минимальный многочлен для z, то все корни z1, z2, … zn уравнения f(x)=0, отличные от z, называют сопряженным с z. Один из корней совпадает с z, будем ставить его на первое место, т.е. z=z1. 2.2 Поле алгебраических чисел В математике , поле алгебраических чисел (или просто номер поля ) является расширение поля в поле из рациональных чисел таким образом, что расширение поля имеет конечную степень (и , следовательно , является алгебраическое расширение поля). Таким образом, поле, которое содержит и имеет конечную размерность, если рассматривать его как векторное пространство . Изучение полей алгебраических чисел и, в более общем смысле, алгебраических расширений поля рациональных чисел является центральной темой теории алгебраических чисел . Понятие поля алгебраических чисел опирается на понятие поля . Поле состоит из набора элементов вместе с двумя операциями, а именно сложением и умножением , а также некоторыми предположениями о дистрибутивности. Яркий пример поля является полем рациональных чисел , обычно обозначаемых , вместе с обычными операциями сложения и умножения[2,с. 74]. Еще одно понятие, необходимое для определения полей алгебраических чисел, - векторные пространства . В той степени, в которой здесь необходимо, векторные пространства можно рассматривать как состоящие из последовательностей (или кортежей ) записи которого являются элементами фиксированного поля, такого как поле . Любые две такие последовательности можно добавить, добавляя записи по одной. Более того, любая последовательность может быть умножена на единственный элемент c фиксированного поля. Эти две операции, известные как сложение векторов и скалярное умножение, удовлетворяют ряду свойств, которые служат для абстрактного определения векторных пространств. Векторные пространства могут быть «бесконечномерными», то есть последовательности, составляющие векторные пространства, имеют бесконечную длину. Если, однако, векторное пространство состоит из конечных последовательностей [3,с. 89]. Поле алгебраических чисел (или просто номер поля ) является конечно- степень расширения поля поля рациональных чисел. Поле алгебраических чисел алгебраически замкнуто, а поле вещественных алгебраических чисел вещественно замкнуто. [1,с.12] Если поле алгебраических чисел К является расширением поля алгебраических чисел F, v - нормирование поля F и w - нормирование поля / С, делящее v, то K. В частности, локальные степени относительно продолжений нормирования v одинаковы. [2,с.14] Элементы поля алгебраических чисел К, которые при любом изоморфизме на сопряженное с К поле вещественных чисел оказываются положительными, называются вполне положительными в К. Если у поля К нет вещественных сопряженных полей, то каждое число из К может быть названо вполне положительным. Понятие вполне положительного числа может быть перенесено на произвольное поле К, если вполне положительными элементами из К назвать такие, которые оказываются положительными при всех упорядочениях на К. [3,с.107] F - поле алгебраических чисел и Ле ( / г), то существует циклическое расширение поля F, расщепляющее алгебру А. Из этого результата вытекает ослабленный вариант следующей теоремы: всякая алгебра А е ( F) эквивалентна циклической. [4,с.10] Галуа над полями алгебраических чисел И.Р.Шафаревичу в 1959 г. была присуждена Ленинская премия. [5,с.96] Если k есть поле алгебраических чисел, то по теореме Мор-деля - Вейля [7] группа 21 имеет конечное число образующих. Тем самым это верно и для Hl ( G, 2lfc); но так как эта группа периодична, то она конечна. [6,с.10] Поле алгебраических чисел алгебраически замкнуто, а поле вещественных алгебраических чисел вещественно замкнуто. [9,с.23] Если поле алгебраических чисел К является расширением поля алгебраических чисел F, v - нормирование поля F и w - нормирование поля / С, делящее v, то K. В частности, локальные степени относительно продолжений нормирования v одинаковы. [10,с.10] Равносторонние триангуляции римановых поверхностей и кривые над полями алгебраических чисел. [11,с96] На этом основании поля конечной степени называются также полями алгебраических чисел, хотя этот термин несколько двусмыслен, не предусматривая обязательно конечность степени. [12,с.17] В качестве этого поля можно, конечно, взять обычное поле R вещественных алгебраических чисел , получающееся путем выделения алгебраических чисел из совокупности всех вещественных чисел. [13,с.17] Общая теория предыдущего параграфа очень хорошо иллюстрируется на примере поля алгебраических чисел. [14,с.96] Кроме того, плотные решетки получаются из идеалов в полях алгебраических чисел. Мы также строим Es и решетку Лича, используя икосианы. [15,с.17] Естественный и важный подход к выделению и изучению тех или иных множеств чисел связан с замкнутостью множеств чисел относительно тех или иных действий. Определение 1: Мы говорим, что некоторое множество чисел М замкнуто относительно некоторого действия, если для всяких двух чисел их М, для которых определен результат данного действия над ним, число, является этим результатом, всегда принадлежащим М. Пример: N Множество натуральных чисел замкнуто относительно сложения, т.к. a, bN (a+b) N. В отношении умножения множество N так же замкнуто. Но оно не является замкнутым относительно вычитания и деления. Действительно: 5, 7 N, но 5-7=-2 N, 3, 2N, но 3:2=1,5 N Множество целых чисел Z замкнуто относительно сложения, вычитания и умножения. Множество чисел вида 2к, кN, замкнуто относительно умножения и деления. 2к×2l=2k+l 2к:2l=2k-l В связи с замкнутостью действий на множестве выделились классы числовых множеств. Рассмотрим один их классов, называемых полем. Определение 2: Множество чисел М, содержащие не менее двух чисел, называется числовым полем, если оно замкнуто относительно действий сложения, вычитания, умножения и деления. Последнее означает, что для любых a, b M, должно иметь место a+b, a-b, a×b M. Так же для любого aM и любого b0 из М, должно выполняться a:bM. Пример: Среди важнейших числовых полей наиболее важными являются: поле всех рациональных чисел; поле всех вещественных чисел; поле всех комплексных чисел. Что касается множества всех целых чисел, то оно не является числовым полем, ибо не замкнуто относительно деления. Существует бесконечно много числовых полей. Нас, в данном случае интересует поле алгебраических чисел. Существуют различные признаки, по которым их общего множества Z выделяю те или иные подмножества, подвергаемые специальному изучению. С точки зрения важного для алгебры понятия алгебраического уравнения, естественным представляется выделение классов чисел, являющихся корнями алгебраических уравнений, коэффициенты которых принадлежат тому или иному классу чисел. Определение 3: Число Z называется алгебраическим, если оно является корнем какого-нибудь алгебраического уравнения с целыми коэффициентами: anxn+an-1xn-1+…+a1x+a0=0 (a0, a1, … ,anZ; an0), т.е. выполняется: anzn+an-1zn-1+…+a1z+a0=0 В определении алгебраического числа можно допустить, чтобы коэффициенты a0, a1, … ,an-1, an были любыми рациональными числами, поскольку, умножив левую и правую части уравнения на целое число, являющиеся общим кратным знаменателем всех коэффициентов, мы получили уравнение с целыми коэффициентами, корнем которого будет наше число. К алгебраическим числам принадлежат, в частности, и все рациональные числа. Действительно, рациональное число z= 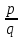 (p, qN) очевидно является корнем уравнения: qx-p=0. (p, qN) очевидно является корнем уравнения: qx-p=0.Также всякое значение корня любой степени из рационального числа является алгебраическим числом. Действительно, число z=  (p, qN) является корнем уравнения:qxn-p=0. (p, qN) является корнем уравнения:qxn-p=0.Существуют и другие алгебраические числа, нежели указанное выше. Пример: Чиcло z=  является алгебраическим. Действительно, возводя в квадрат обе части равенства, определяющего число z, получим: z2=2+2 является алгебраическим. Действительно, возводя в квадрат обе части равенства, определяющего число z, получим: z2=2+2 +3. Отсюда z2-5= +3. Отсюда z2-5= . Возводя в квадрат обе части этого равенства, получим: z4-10z2+25=24. Отсюда следует, что число z является корнем следующего уравнения: . Возводя в квадрат обе части этого равенства, получим: z4-10z2+25=24. Отсюда следует, что число z является корнем следующего уравнения:x4-10x2+1=0 Всякое число z=a+bi, у которого компоненты a и b – рациональные числа, являются алгебраическими. Докажем это. 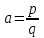 , ,  (p, q, (p, q,  N). N).Из равенства  , получаем: , получаем:  . Отсюда, возводя в квадрат, получим: . Отсюда, возводя в квадрат, получим:  . Следовательно, я является корнем уравнения: . Следовательно, я является корнем уравнения: все коэффициенты которого целые числа. В дальнейшем мы будем рассматривать только действительные алгебраические числа, не оговаривая этого каждый раз. Из f(x)=0 следует f(z)(x)=0, где в качестве (x) можно взять любой многочлен с целыми коэффициентами. Таким образом для любого алгебраического числа z, из всех этих многочленов обычно рассматривают многочлен наименьшей степени. Определение 4: Число n называется степенью алгебраического числа z, если z есть корень некоторого многочлена n-ой степени с рациональными коэффициентами и не существует тождественно не равного нулю многочлена с рациональными коэффициентами степени, меньшей чем n, корнем которого является z. Если корень многочлена n-ой степени с целыми рациональными коэффициентами z не является корнем ни одного тождественно неравного нулю многочлена с целыми коэффициентами степени меньшей чем n, то z не может быть корнем и тождественно неравного нулю многочлена с рациональными коэффициентами степени меньшей чем n, т.е. z – алгебраическое число степени n. Рациональные числа являются алгебраическими числами первой степени. Любая квадратическая иррациональность представляет собой алгебраическое число 2-й степени, так как, являясь корнем квадратичного уравнения с целыми коэффициентами, она не является корнем какого-либо уравнения 1-й степени с целыми коэффициентами. Алгебраические числа 3-й степени часто называют кубическими иррациональностями, а 4-й степени биквадратическими иррациональностями. Пример:  - алгебраическое число 3-й степени, т.е. кубическая иррациональность. Действительно, это число есть корень многочлена 3-й степени с целыми коэффициентами x3-2=0 и - алгебраическое число 3-й степени, т.е. кубическая иррациональность. Действительно, это число есть корень многочлена 3-й степени с целыми коэффициентами x3-2=0 и  не является корнем какого-либо многочлена 1-й или 2-й степени с целыми коэффициентами. не является корнем какого-либо многочлена 1-й или 2-й степени с целыми коэффициентами.Определение 5: Если алгебраическое число n-й степени z является корнем многочлена f(x)=xn+b1xn-1+ … +bn (n1) (1) с рациональными коэффициентами, то f(x) называется минимальным многочленом для z. Таким образом, минимальным многочленом для z называется многочлен наименьшей степени с рациональными коэффициентами и старшим коэффициентом, равном единице, корнем которого является z. Если вместо многочлена (1) взять какой-либо другой многочлен с рациональными коэффициентами степени n, корнем которого является z, то многочлен (1) может быть получен из него делением всех коэффициентов на старший член. Пример: Минимальным многочленом для  является x3-2, так как корень этого многочлена является x3-2, так как корень этого многочлена  не является корнем какого-либо многочлена степени с рациональными коэффициентами. не является корнем какого-либо многочлена степени с рациональными коэффициентами.Теорема 1: Если f(x) минимальный многочлен алгебраического числа z и f(x) многочлен с рациональными коэффициентами, такой, что F(z)=0, то f(x) делитель F(x), т.е. F(x)=f(x)g(x), где g(x) также многочлен с рациональными коэффициентами. Доказательство: Согласно известной теореме алгебры F(x) можно представить в виде: F(x)=f(x)g(x)+r(x) где g(x) и к(ч) – многочлены с рациональными коэффициентами, причем степень r(x) меньше степени f(x). Поскольку F(x)=0 и f(z)=0, то придавая x значение z, получаем r(z)=0; z – корень многочлена r(x) с рациональными коэффициентами степени, меньшей чем у минимального для z многочлена, т.е. меньшей чем степень z. Это может быть только если r(x) тождественно равен нулю, а значит F(x)=f(x)g(x). Теорема доказана. Теорема 2: Для любого алгебраического числа z минимальный многочлен неприводим над полем рациональных чисел. Доказательство: Пусть f(x) – минимальный многочлен для z. Предположим, что f(x) приводим над полем рациональных чисел, т.е., что f(x)=(x)(x), (x)(x) – многочлены с рациональными коэффициентами, степени меньшей, чем n. Из равенства (x)(x)=f(x)=0 следует, что из двух чисел (x) и (x), по крайней мере одно равно нулю. Пусть например (x)=0, тогда z – корень тождественно не равного нулю многочлена (x) с рациональными коэффициентами, степени меньшей, чем n, т.е. меньшей чем у f(x). А это противоречит тому, что f(x) – минимальный многочлен для z. Предположение, что f(x) приводим над полем рациональных чисел, оказалось неверным, т.е. f(x) неприводим над этим полем. Теорема доказана. Теорема 3: Если z корень неприводимого над полем рациональных чисел многочлена F(x) с рациональными коэффициентами степени n, то z – алгебраическое число степени n. Доказательство: Обозначим минимальный многочлен для z через f(x). Согласно теоремы 1: F(x)=f(x)g(x); где g(x) – многочлен с рациональными коэффициентами. Поскольку F(x) неприводим над полем рациональных чисел и f(x) отлично от постоянного, то g(x)=c, где c – рационально. F(x)=cf(x), т.е. z – алгебраическое число n-й степени. Теорема доказана. Пример: Пусть p – простое число.  при любом простом целом a (a>1), не равном p-ой степени другого целого, представляет собой алгебраическое число степени p. Действительно это число есть корень неприводимого над полем рациональных чисел многочлена. при любом простом целом a (a>1), не равном p-ой степени другого целого, представляет собой алгебраическое число степени p. Действительно это число есть корень неприводимого над полем рациональных чисел многочлена.xp-a=0 Если z – алгебраическое число степени n и f(x) – минимальный многочлен для z, то все корни z1, z2, … zn уравнения f(x)=0, отличные от z, называют сопряженным с z. Один из корней совпадает с z, будем ставить его на первое место, т.е. z=z1. Теорема 4: Множество всех действительных алгебраических чисел представляет собой поле, т.е. сумма, разность, произведение и частное двух алгебраических чисел и (для частного при 0) являются алгебраическими числами. Доказательство: Пусть - корень многочлена f(x) степени n с целыми коэффициентами, корни которого 1, 2, … ,n, и - корень многочлена (x) степени m с целыми коэффициентами, корни которого 1, 2, … m (=1). Рассмотрим многочлен: F(x)= 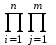 (x-(i+i))= (x-(i+i))== (x-1-1) (x-1-2) … (x-1-m) (x-2-1) (x-2-2) … (x-2-m) (x-n-1) (x-n-2) … (x-n-m) Если в этом произведении сделать какую угодно подстановку величин 1, 2, … ,n, то некоторые строки переставляется местами, но произведение в целом не изменится. Это значит, что F(x) – симметрический многочлен по отношению 1, 2, … m. В целом F(x) – симметрический многочлен от двух систем аргументов: 1, 2, … ,n и 1, 2, … m. Согласно известным теоремам о симметрических многочленах, коэффициенты многочлена F(x) могут быть выражены рационально через элементарные симметрические функции от 1, 2, … ,n и 1, 2, … m, т.е. через целые коэффициенты, f(x) и (x). Это значит, что коэффициенты F(x) рациональны, и, следовательно, число +=1+1, являющегося, как это непосредственно видно из формулы, корнем F(x), есть алгебраическое число. Для доказательства того, что произведение двух алгебраических чисел и есть алгебраическое число, достаточно, аналогично тому, как это было только что сделано для многочлена, рассмотреть многочлен: F(x)= 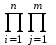 (x-ii) (x-ii) Этот многочлен имеет в качестве одного из своих корней 11=. Пусть - корень многочлена (x)=b0xn+ b1xn-1+ … bn, (bi – целые числа). Тогда - является корнем многочлена с целыми коэффициентами. (-x)=(-1)nb0xn+(-1)n-1b1xn-1+ … bn, а при 0 корень многочлена xn( 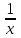 )=b0+b1x+ … bnxn. Таким образом, вместе с алгебраическими числами являются - и )=b0+b1x+ … bnxn. Таким образом, вместе с алгебраическими числами являются - и  . .Разность может быть представлена в виде +(-), т.е. в виде суммы двух алгебраических чисел. При 0 частное 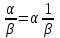 , являясь произведением двух алгебраических чисел, представляет собой так же алгебраическое число. , являясь произведением двух алгебраических чисел, представляет собой так же алгебраическое число.Если степени алгебраических чисел и равны m и n, то, взяв в качестве f(x) и (x) соответствующие минимальные многочлены будем в (2) и (3) иметь многочлены степени mn, и алгебраические числа степени, не большей, чем mn. Многочлены (x), (-x), и xn  одинаковой степени, а, следовательно, , -, одинаковой степени, а, следовательно, , -,  - алгебраические числа одной и той же степени, откуда следует, что и - и - алгебраические числа одной и той же степени, откуда следует, что и - и  имеют степени не больше, чем mn. Теорема доказана. имеют степени не больше, чем mn. Теорема доказана.Пример: 1) 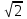 и и  алгебраические числа 2-й степени, а алгебраические числа 2-й степени, а  - алгебраическое число 4 степени. Действительно, если = - алгебраическое число 4 степени. Действительно, если = , то 2=5+ , то 2=5+ , 24-102+1=0, т.е. корень многочлена f(x)=x4-10x2+1 с целыми коэффициентами, и f(x)=(x- , 24-102+1=0, т.е. корень многочлена f(x)=x4-10x2+1 с целыми коэффициентами, и f(x)=(x- )(x- )(x- )(x+ )(x+ )(x+ )(x+ ) ) Из теоремы единственности над полем рациональных чисел множители f(x) должны являться произведением каких-то множителей правой части равенства (4). Легко видеть, что из этих множителей нельзя составить многочлен с рациональными коэффициентами степени меньшей, чем 4, т.е. f(x) – неприводимый над полем рациональных чисел многочлен, а, следовательно, согласно теореме 3,  - алгебраическое число 4-й степени. - алгебраическое число 4-й степени.2) =  и = и = , как легко видеть, это алгебраические числа 6-й степени, а произведение = , как легко видеть, это алгебраические числа 6-й степени, а произведение = - алгебраическое число 3-й степени. - алгебраическое число 3-й степени.Заключение Алгебраические числа имеют широкое применение в теории чисел, алгебре, геометрии и других разделов математики. Они позволяют раскрыть вариантности алгебры для практических приложений. Это имеет большое значение в подготовке учителя для средней школы. Изучение свойств таких чисел составляет содержание одного из важнейших разделов современной теории чисел, называемого алгебраической теорией чисел. К этому разделу относятся вопросы, связанные с изучением различных классов алгебраических чисел. Эта работа может служить в качестве учебного пособия при изучении теории алгебраических чисел. А так же она удобна в использовании при подготовке к экзамену. В работе введена сплошная нумерация теорем и определений арабскими цифрами. Все теоремы даны с полными доказательствами. Приведенные примеры алгебраических чисел и действий над ними, даны с доступными пояснениями и, при необходимости, с доказательством. Большое место в работе занимают теоретические сведения о развитии алгебры теории чисел. Помимо введения, дающего общий очерк развития теории чисел, первый параграф посвящен уже конкретно развитию теории алгебраических чисел. Так же на протяжении всей работы можно наблюдать исторические комментарии. Данная работа дает представление о современном состоянии рассматриваемого вопроса и дает представление о теории алгебраических чисел и о теории чисел вообще, как о развивающейся науке. Список использованных источников 1. Айерлэнд, К. Классическое введение в современную теорию чисел / К. Айерлэнд, М. Роузен. - М.: Мир, 1987. - 416 c. 2. Алфутова, Н. Б. Алгебра и теория чисел. Сборник задач / Н.Б. Алфутова, А.В. Устинов. - М.: МЦНМО, 2002. - 264 c. 3. Алфутова, Н. Б. Алгебра и теория чисел. Сборник задач / Н.Б. Алфутова, А.В. Устинов. - Москва: Высшая школа, 2009. - 336 c. 4. Алфутова, Н.Б. Алгебра и теория чисел: Сборник задач для математических школ / Н.Б. Алфутова, А.В. Устинов. - М.: [не указано], 2003. - 930 c. 5. Введение в современную теорию чисел. - М.: Московский центр непрерывного математического образования (МЦНМО), 2013. - 600 c. 6. Вейль, Г. Алгебраическая теория чисел / Г. Вейль. - Москва: ИЛ, 2011. - 224 c. 7. Виленкин, Н.Я. Алгебра и теория чисел / Н.Я. Виленкин. - М.: Книга по Требованию, 2012. - 192 c. 8. Гильберт, Д. Избранные труды. В 2 томах. Том 1. Теория инвариантов. Теория чисел. Алгебра. Геометрия. Основания математики / Д. Гильберт. - М.: Факториал, 1998. - 576 c. 9. Дэвенпорт, Г. Высшая арифметика. Введение в теорию чисел / Г. Дэвенпорт. - Москва: СИНТЕГ, 2010. - 243 c. 10. Дэвенпорт, Г. Высшая арифметика. Введение в теорию чисел. / Г. Дэвенпорт. - М.: [не указано], 2017. - 546 c. 11.Л.Я. Куликов «Алгебра и теория чисел» М.: Высшая школа, 1979. — 559 с. 12. Александр Бухштаб: Теория чисел. Учебное пособие, 1966 г. 13. Основы теории чисел: Учебное пособие. 11-е изд.,стер. — СПб.: Издательство «Лань», 2006. — 176 с. —(Учебники для вузов. Специальная литература). 14. Винберг Э.Б. Алгебра многочленов. - М., Просвещение, 1980. - 176 с. 15. Варден, Бартел Лендерт ван дер. Алгебра [Текст] / Пер. с нем. А. А. Бельского ; Под ред. Ю. И. Мерзлякова. - Москва : Наука, 1976. - 648 с. 16. Э.Ф. Шмигирев, С.В. Игнатович. Теория многочленов. Мозырь 2002. |
