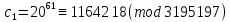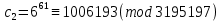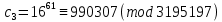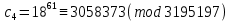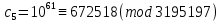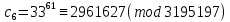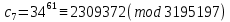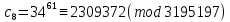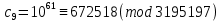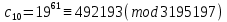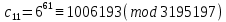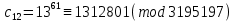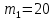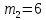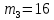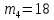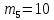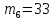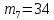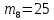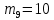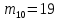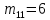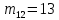Применение теории чисел в криптосистеме RSA. статья_Шадрин. Применение теории чисел в криптосистеме rsa
 Скачать 24.64 Kb. Скачать 24.64 Kb.
|
|
Применение теории чисел в криптосистеме RSA Математика неизменно является обязательной дисциплиной любой образовательной программы, будь то школа или университет. В силу абстрактного характера этой дисциплины, у большинства учащихся рано или поздно возникает естественный вопрос – есть ли реальное применение изучаемой ими математической теории? Несмотря на очевидность ответа, привести убедительные примеры реального применения математической теории на практике не так просто. Главной причиной этого является текущий уровень владения математической теорией самими учащимися, недостаточный для понимания ее практических приложений. Как сказал Л.Д. Кудрявцев, «сама математика является абстрактной наукой, а ее применения могут быть весьма конкретными. При этом следует помнить, что нельзя обучить приложениям математики, не научив самой математике» ([3], с. 60). Поэтому проблема поиска примеров приложений математических теорий, сочетающих в себе, с одной стороны, простоту их теоретических основ, а с другой стороны, большую практическую значимость в современном мире, является очень актуальной и в настоящее время. Ярким и неоспоримым примером практического применения результатов «чистой» математики в реальной жизни является, на наш взгляд, изучение современных криптографических алгоритмов. Криптография – наука о математических методах обеспечения конфиденциальности (невозможности прочтения информации посторонним) и аутентичности (целостности и подлинности авторства) информации. Другими словами, криптография изучает методы преобразования (шифрования) информации с целью ее защиты от незаконных пользователей при хранении информации в ненадежных источниках или передачи ее по незащищенным каналам связи. В последние десятилетия, когда человечество вступило в стадию информационного общества, роль криптографии резко возросла. Её методы, начиная от электронной почты и заканчивая банковскими системами, широко используются государственными структурами, юридическими и частными лицами в электронных коммерческих операциях, при идентификации, аутентификации и так далее. При этом все современные криптографические алгоритмы базируются на результатах классической теории чисел, поэтому идеи и методы, лежащие в их основе, доступны для понимания студентам младших курсов и даже школьникам. В данной работе приведем пример применения теории чисел в криптографической системе с открытым ключом RSA, с помощью которого решается задача шифрования и дешифрования информации в этой системе. Тысячелетиями в криптографии для шифровки и дешифровки сообщений использовался один и тот же ключ. Главной проблемой при этом являлось обеспечение секретности используемого ключа, потому что любое обладающее им лицо может использовать его для расшифровки данных. Идея криптосистемы с открытым ключом, при которой для шифровки и дешифровки сообщений используются разные ключи, и более того – ключ, используемый для дешифровки, находится в открытом доступе, впервые была озвучена в ноябре 1976 года, в публикации Уитфилда Диффи и Мартина Хеллмана «Новые направления в криптографии» [1], благодаря которой была открыта новая область в криптографии – криптография с открытым ключом. Первой криптосистемой с открытым ключом принято считать алгоритм RSA (аббревиатура от фамилий Rivest, Shamir, Adleman). Некоторое время принцип работы алгоритма оставался засекреченным. Однако, в феврале 1978 года в журнале «Communications of the ACM» было опубликовано полное описание новой криптосистемы. В 1989 году алгоритм RSA находит применение в зарождающейся сети интернет, а в 1990 году алгоритм начинает использовать министерство обороны США. Основу криптографической системы RSA составляет теория сравнений. Ознакомиться с основными положениями теории сравнений, необходимыми для понимания дальнейшего текста, можно, к примеру, в [2] или в [4]. Вопрос применения теории чисел в криптосистеме RSA достаточно подробно раскрыт в монографии [5]. Описание алгоритма можно найти, к примеру, в [6]. Рассмотрим пример шифрования и дешифрования информации с помощью криптографической системы RSA и покажем, что основу алгоритма составляет теория чисел. Закодируем, например, словосочетание «Теория чисел». Изначально будет считать, что регистр букв не имеет значения, а каждой букве присвоен ее порядковый номер в алфавите.
Этап создания ключей: Выберем два простых числа 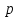 и и 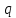 , причем таких, что , причем таких, что 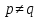 . Пусть . Пусть 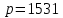 и и 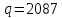 . .Вычислим произведение взятых чисел: 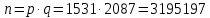 . .Вычислим функцию Эйлера для полученного числа по формуле 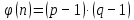 . Тогда . Тогда 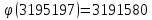 . .Выберем произвольное число 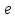 . Пусть . Пусть 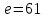 . .С помощью алгоритма Евклида вычислим число d, удовлетворяющее условию 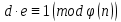 . Получим, . Получим, 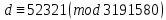 . .Переходим к этапу распределения ключей. Назначаем пару 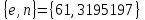 в качестве открытого ключа/ в качестве открытого ключа/Назначаем пару 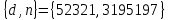 в качестве закрытого ключа. в качестве закрытого ключа.Теперь, когда в наличии имеются открытый и закрытый ключи, можно приступать к этапу шифрования. Выбираем текст, который необходимо зашифровать (шифрование будем выполнять с помощью открытого ключа). В нашем примере текст «Теория чисел» состоит из двенадцати символов 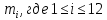 . . Шифруем сообщение с использованием открытого ключа получателя по формуле: 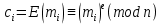 . .
Заключительным этапом будет этап дешифрования. Возьмем полученный зашифрованный текст 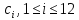 и дешифруем его с помощью закрытого ключа по формуле: и дешифруем его с помощью закрытого ключа по формуле: 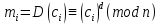 . .
Осталось лишь поставить в соответствие каждой букве ее порядковый номер и получить исходный текст: «Теория чисел». Конечно, в реальных условиях при шифровании и дешифровании алгоритмом RSA применяются числа, превосходящие рассмотренные в несколько раз, чем и достигается высокая криптостойкость данного алгоритма. Таким образом, нами приведен пример приложения теории чисел, имеющий огромное практическое значение в современном мире. Из него ясно, что идеи, лежащие в его основе, доступны для усвоения уже студентами первого курса математических направлений, поэтому могут являться завершающей темой при изучении курса теории чисел. И даже больше, в силу того, что рассматриваемый в данной работе вопрос имеет реальное практическое применение, к его рассмотрению можно приступить в старших классах общеобразовательной школы, поскольку он вполне доступен для восприятия. Знакомство школьников с теорией чисел можно начать на дополнительных занятиях, представляющих собой факультативный или элективный курс. Поскольку в рамках курса большое внимание будет уделяться применению теории чисел в криптосистеме RSA, то стоит более детально рассмотреть вопросы теории сравнений и теории делимости чисел. После усвоения основных положений теории чисел, в частности, теории сравнений, школьникам предстоит познакомиться с криптографической системой RSA, историей ее возникновения, описанием алгоритма и принципом ее работы. Завершающим этапом работы станет шифрование и дешифрование информации с помощью криптосистемы RSA. Данную работу можно провести в форме контрольной работы. Таким образом, рассмотренный нами пример приложения теории чисел в криптосистеме RSA может является великолепной основой элективного математического курса для учащихся старших классов общеобразовательных школ. Литература: Diffie W., Hellman M. E. New Directions in Cryptography / IEEE Trans. Inf. Theory / F. Kschischang — IEEE, 1976. — Vol. 22, Iss. 6. — P. 644–654. Коутинхо, С. Введение в теорию чисел. Алгоритм RSA. / С. Коутинхо – М., 2001. – 328 с. Кудрявцев, Л.Д. Современная математика и ее преподавание. / Л.Д. Кудрявцев – М., 1985. – 168 с. Манин, Ю.И. Введение в современную теорию чисел. / Ю.И. Манин, А.А. Панчишкин – М., 2009. – 552 с. Нестеренко, Ю.В. Теория чисел. / Ю.В. Нестеренко – М., 2008. – 272 с. Романьков, В.А. Алгебраическая криптография. / В.А. Романьков - Омск, 2013. – 136 с. |

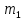 =«т»=20
=«т»=20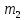 =«е»=6
=«е»=6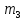 =«о»=16
=«о»=16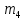 =«р»=18
=«р»=18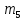 =«и»=10
=«и»=10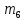 =«я»=33
=«я»=33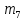 =«_»=34
=«_»=34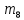 =«ч»=25
=«ч»=25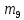 =«и»=10
=«и»=10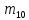 =«с»=19
=«с»=19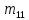 =«е»=6
=«е»=6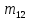 =«л»=13
=«л»=13