лр5. К лабораторной 5 (2). Методы анализа временных рядов
 Скачать 0.75 Mb.
|
|
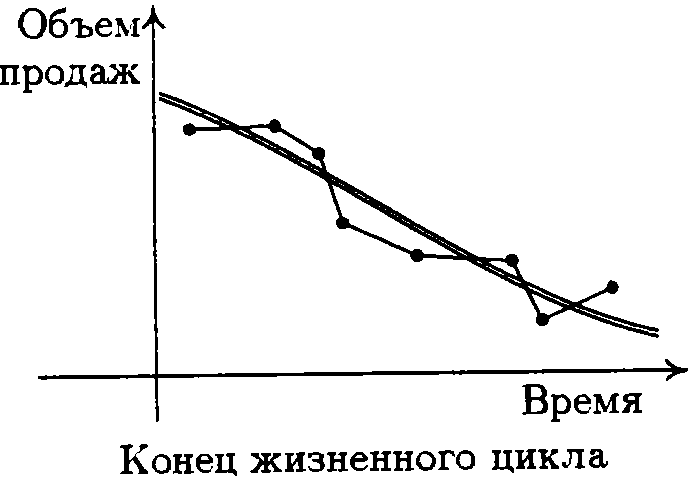
Лабораторная работа №5 Тема: Методы анализа временных рядов Цель: Приобрести навыки прогнозирования значений временного ряда, в частности, выделения тренда и учета сезонной составляющей, а также навыки использования средств Пакет Анализа и Поиск решения, входящих в MS Excel. Порядок выполнения работы: 1) Прогнозирование значений временного ряда. Для каждой задачи необходимо: Изучить теорию. Построить график значений временного ряда. Построить графики прогнозируемых значений (для каждого из полученных прогнозов). Вычислить САО или СООП Ответить на вопросы задачи. 2) Составление отчёта по лабораторной работе, в котором представляется: формулировка индивидуального задания; ответы на вопросы задачи; при необходимости, снимки экрана монитора, содержащие основные моменты решения задачи; графики значений временного ряда и прогноза. Теория Временным рядом называется последовательность значений некоторого показателя во времени (например, объемов продаж, как на рис. 1). 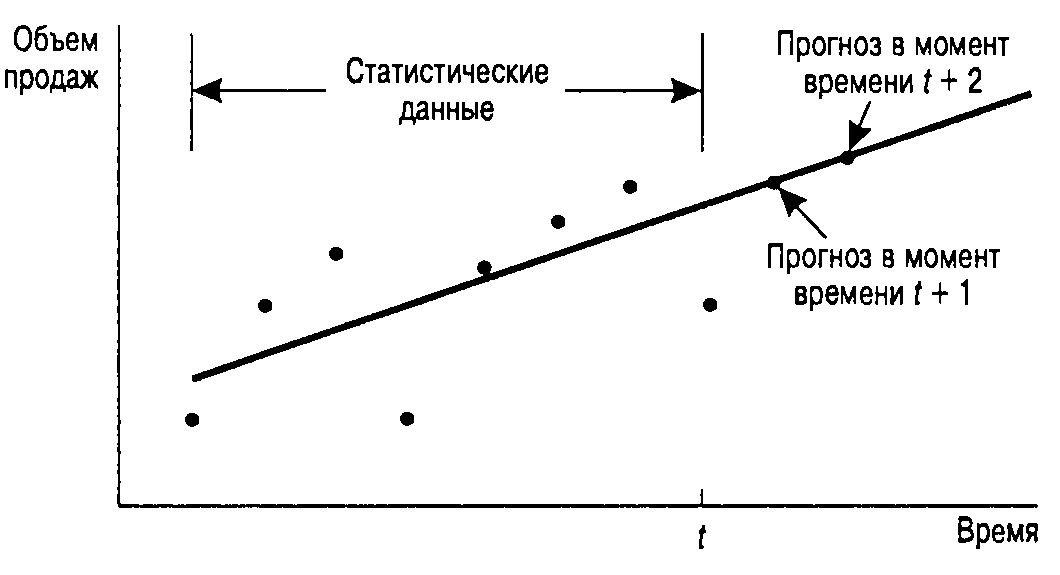 Рис. 1 Анализ временных рядов является способом выявления тенденций прошлого и продления их в будущее. Методы анализа временных рядов осуществляют прогноз путем экстраполяции значений отдельной переменной на основе статистических данных за прошлый временной период. Основное допущение, которое при этом делается, заключается в том, что происшедшее в прошлом дает хорошее приближение в оценке будущего. Развитие процессов, реально наблюдаемых в жизни, складывается из некоторой устойчивой тенденции (тренда) и некоторой случайной составляющей, выражающейся в колебании значений показателя вокруг тренда. На рис. 2 показано, как могут зависеть объемы продаж одного и того же товара на двух стадиях его жизненного цикла (в начале и в конце продаж).
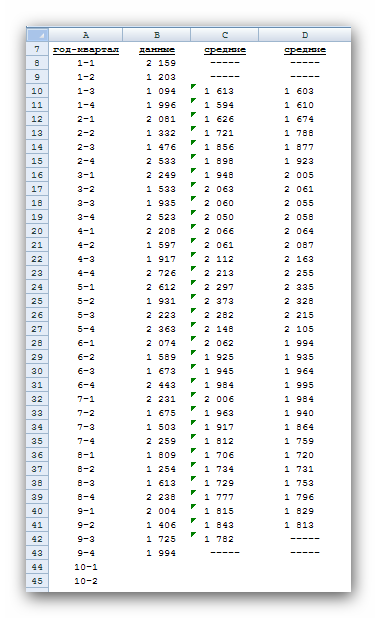
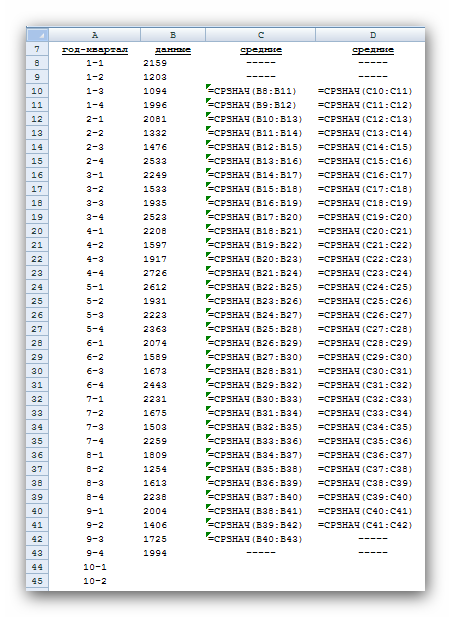
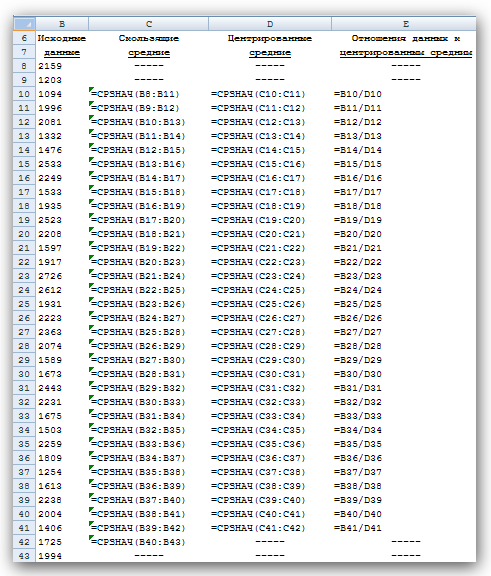
Рис. 2 Кривые тренда сглаживают временной ряд значений показателя, выделяя общую тенденцию. Именно выбор кривой тренда во многом определяет результаты прогнозирования. В большинстве случаев временной ряд, кроме тренда и случайных отклонений от него, характеризуется еще сезонной составляющей. Сезонная составляющая — это периодические изменения показателя. Обычная продолжительность сезонной составляющей измеряется днями, неделями или месяцами. Вначале рассмотрим несколько простейших методов прогнозирования, не учитывающих наличия сезонности во временном ряде. Предположим, что в журнале Wall Street Journal приведена сводка за последние 12 дней (включая сегодняшний) цен на апельсины, сложившихся на момент закрытия биржи. Используя эти данные, нужно предсказать завтрашнюю цену на какао (также на момент закрытия биржи). Рассмотрим несколько способов сделать это. Если последнее (сегодняшнее) значение наиболее значимо по сравнению с остальными, то оно является наилучшим прогнозом на завтра. Возможно, из-за быстрого изменения цен на бирже первые шесть значений уже устарели и не актуальны, в то время как последние шесть значимы и имеют равную ценность для прогноза Тогда в качестве прогноза на завтра можно взять среднее последних шести значений. Если все значения существенны, но сегодняшнее 12-е значение наиболее значимо, а предыдущие 11-е, 10-е, 9-е и т.д. имеют все меньшую и меньшую значимость, следует найти взвешенное среднее всех 12 значений. Причем весовые коэффициенты для последних значений должны быть больше, чем для предыдущих, и сумма всех весовых коэффициентов должна равняться 1. Первый способа называется «наивным» прогнозом и достаточно очевиден. Рассмотрим подробнее остальные способы. Метод скользящего среднего. Одним из предположений, лежащих в основе данного метода, является то, что более точный прогноз на будущее можно получить, если использовались недавние наблюдения, причем, чем «новее» данные, тем их вес для прогноза должен быть больше. Удивительно, но такой «наивный» подход оказывается чрезвычайно полезным для практики. Например, многие авиакомпании используют частный тип скользящего среднего для создания прогнозов спроса на авиаперелеты, которые, в свою очередь, используются в сложных механизмах управления и оптимизации доходов. Более того, практически все программные пакеты управления запасами содержат модули, выполняющие прогнозы на основе того или иного типа скользящего среднего. Рассмотрим следующий пример. Менеджеру нужно спрогнозировать спрос на производимые его компанией станки. Данные по объемам продаж за последний год работы компании находятся в файле Станки.xls. Простое скользящее среднее. В этом методе среднее фиксированного числа N последних наблюдений используется для оценки следующего значения временно ряда. Например, используя данные о продажах станков за первые три месяца года, менеджер получает для апреля значение  .В случае произвольного числа N узлов расчетная формула выглядит так  .Менеджер вычислил объем продаж на основе простого скользящего среднего за 3 и 4 месяца. Но какое количество узлов даст более точный прогноз? Для оценки точности прогнозов используются среднее абсолютных отклонений (САО) и среднее относительных ошибок, в процентах (СООП), вычисляемые по формулам 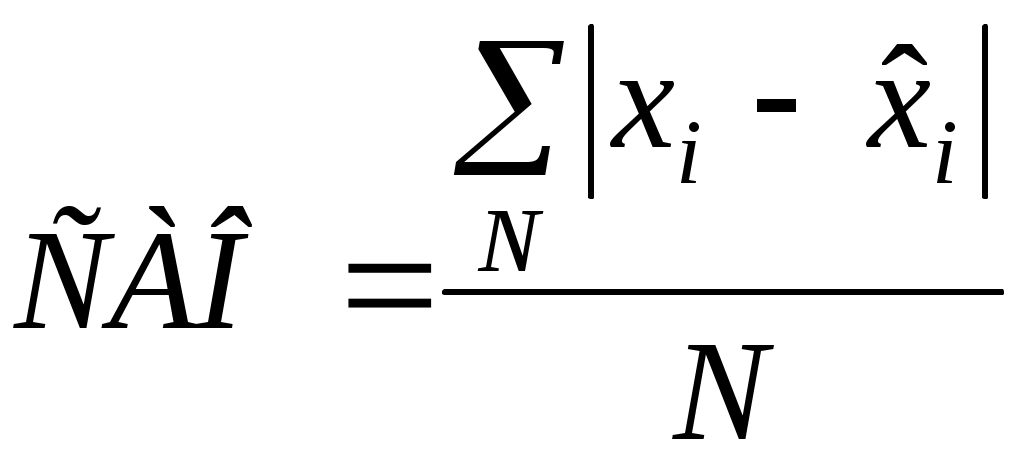 , ,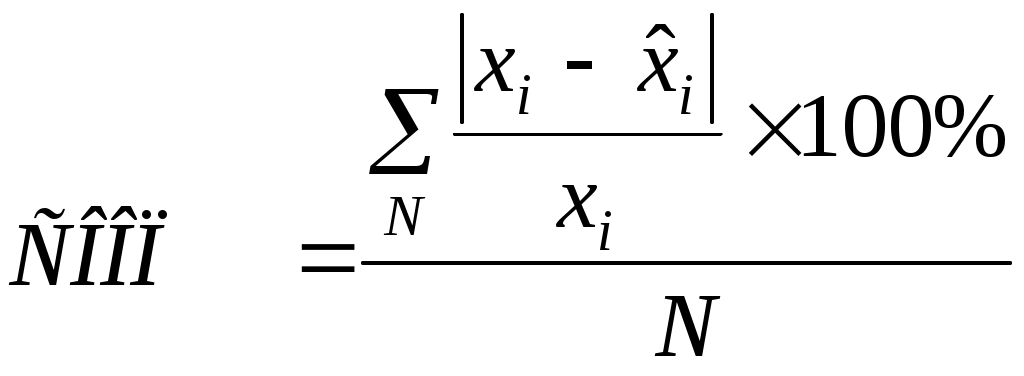где N — количество прогнозов. Согласно результатам, полученным на листе «Простое ск. среднее» рабочей книги Станки.xls (рис. 3), скользящее среднее за три месяца имеет значение САО равное 12,67 (ячейка D16), тогда как для скользящего среднего за 4 месяца значение САО равно 15,59 (ячейка F16). Это значит, что использование большего количества статистических данных скорее ухудшает, чем улучшает точность прогноза методом скользящего среднего. 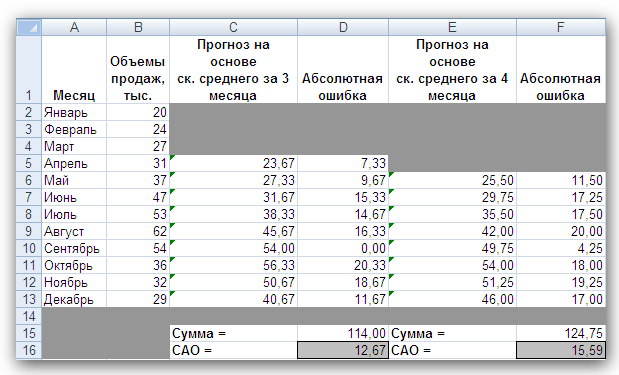 Рис. 3 На графике (рис. 4), построенном по результатам наблюдений и прогнозов с интервалом 3 месяца, можно заметить ряд особенностей, общих для всех применений метода скользящего среднего. 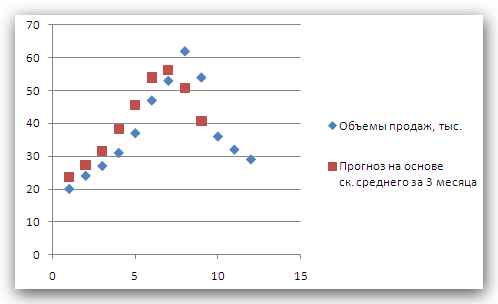 Рис. 4 Значение прогноза, полученное методом простого скользящего среднего, всегда меньше фактического значения, если исходные данные монотонно возрастают, и больше фактического значения, если исходные данные монотонно убывают. Поэтому, если данные монотонно возрастают или убывают, то с помощью простого скользящего среднего нельзя получить точных прогнозов. Этот метод лучше всего подходит для данных с небольшими случайными отклонениями от некоторого постоянного или медленно меняющегося значения. Основной недостаток метода простого скользящего среднего возникает в результате того, что при вычислении прогнозируемого значения самое последнее наблюдение имеет такой же вес (т. е. значимость), как и предыдущие. Это происходит потому, что вес всех N последних наблюдений, участвующих в вычислении скользящего среднего, равен 1/N. Присвоение равного веса противоречит интуитивному представлению о том, что во многих случаях последние данные могут больше сказать о том, что произойдет в ближайшем будущем, чем предыдущие. Взвешенное скользящее среднее. Вклад различных моментов времени можно учесть, вводя вес для каждого значения показателя в скользящем интервале. В результате приходим к методу взвешенного скользящего среднего, который математически можно записать так 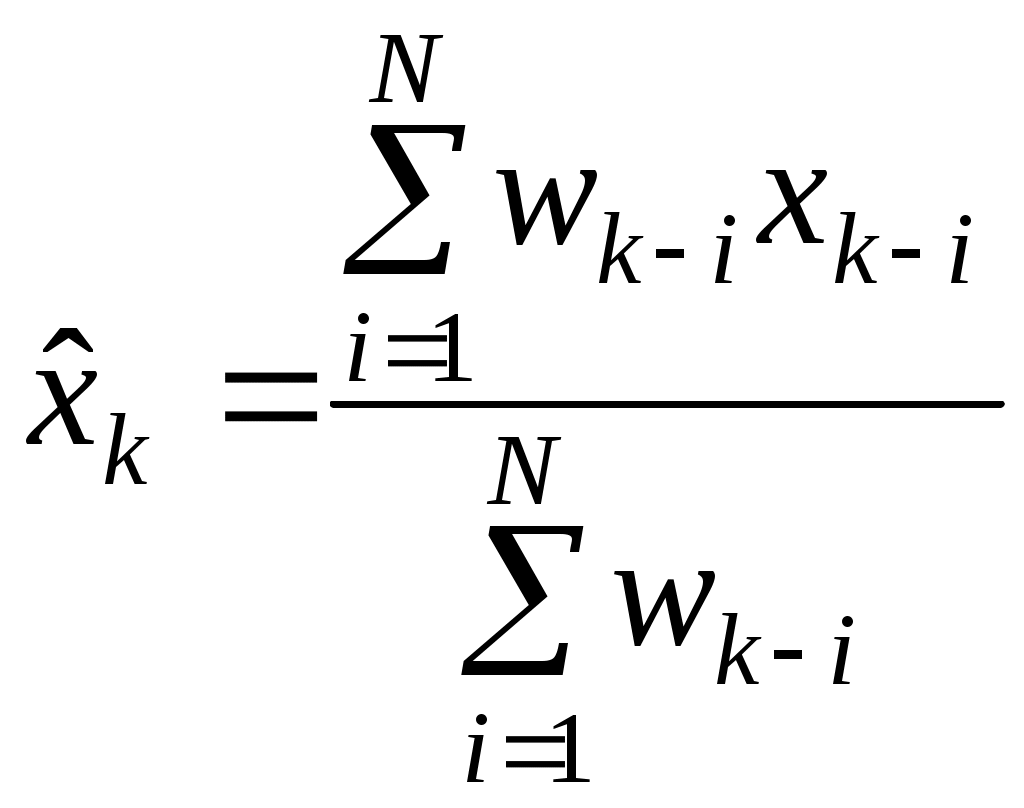 ,где  — вес, с которым используется показатель  при расчете.Вес — это всегда положительное число. В случае, когда все веса одинаковы, мы возвращаемся к простому скользящему среднему. Теперь наш менеджер может использовать метод взвешенного скользящего среднего за 3 месяца. Но как ему выбрать веса? Конечно, это всегда можно сделать «методом проб и ошибок», выбирая веса произвольно, и оценивая точность прогноза при помощи САО (САО меньше, точность прогноза выше). Однако, пробы и ошибки могут продолжаться довольно долго. Есть более простой путь. Используя средство Поиск решения, можно определить оптимальный вес узлов. Чтобы определить вес узлов с помощью средства Поиск решения, при котором значение среднего абсолютных отклонений было бы минимально, выполните такие действия Выберите команду Сервис -> Поиск решения. В открывшемся диалоговом окне Поиск решения установите ячейку G16 целевой (см. лист «Веса») и укажите, что ее значение должно быть минимальным. В поле Изменяя ячейки введите диапазон В1:В3. Введите ограничения В4 = 1,0, В1:ВЗ ≥ 0, В1:В3 ≤ 1, B1 ≤ В2 и В2 ≤ В3. Щелкнув на кнопке Выполнить, получите результат, показанный на рис. 5. 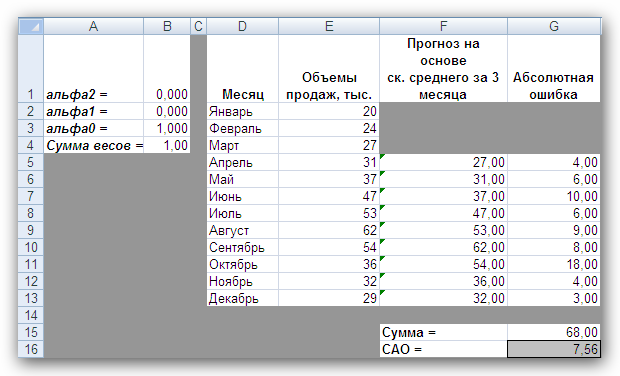 Рис. 5 Полученные результаты показывают, что оптимальное распределение весов таково, что весь вес сосредоточен на самом последнем наблюдении, при этом значение среднего абсолютных отклонений равно 7,56. Этот результат подтверждает предположение о том, что более поздние наблюдения должны иметь больший вес. Прогнозы в методах скользящего среднего зависят от предыдущих значений показателя временного ряда, но не от качества предыдущих прогнозов. Рассмотрим метод один из методов прогнозирования, который учитывает отклонение предыдущего прогноза от реального значения показателя ряда. Метод экспоненциального сглаживания. Очевидно, что в методе взвешенного скользящего среднего существует множество способов задавать значения весов так, чтобы их сумма была равной 1. Один из таких способов называется экспоненциальным сглаживанием. В этой схеме метода взвешенного среднего для любого t > 1 прогнозируемое значение  в момент времени t+1 представляет собой взвешенную сумму фактического объема продаж  , за период времени t и прогнозируемого объема продаж  , за период времени t Другими словами, .Экспоненциальное сглаживание имеет вычислительные преимущества перед скользящим средним. Здесь, чтобы вычислить , необходимо знать только значения , и , (а также значение α), вместо значений показателя ряда во всех узлах, по которым происходит сглаживание. Сохраняя значение α и последний прогноз, мы также неявно сохраняем и все предыдущие прогнозы.Рассмотрим некоторые свойства модели экспоненциального сглаживания. Для начала заметим, что если t > 2, то в формуле (1) t можно заменить на t–1, т.е.  Подставив это выражение в первоначальную формулу (1), получим .Выполняя последовательно аналогичные подстановки, получим следующее выражение для   .Поскольку из неравенства 0 < α < 1 следует, что 0 < 1 – α < 1, то  Другими словами, наблюдение , имеет больший вес, чем наблюдение  , которое, в свою очередь, имеет больший вес, чем  . Это иллюстрирует основное свойство модели экспоненциального сглаживания — коэффициенты при  убывают при уменьшении номера k. Также можно показать, что сумма всех коэффициентов (включая коэффициент при  ), равна 1.Из приведенной формулы видно также, что значение является взвешенной суммой всех предыдущих наблюдений (включая последнее наблюдение ). Последнее слагаемое этой суммы является не статистическим наблюдением, а «предположением»  (можно предположить, например, что  ). Очевидно, что с ростом t влияние , на прогноз уменьшается, и в определенный момент им можно будет пренебречь. Даже если значение α достаточно малое (такое, что (1 – α) приблизительно равно 1), значение  будет быстро убывать.Значение параметра α сильно влияет на функционирование модели прогнозирования, поскольку α представляет собой вес самого последнего наблюдения . Это значит, что следует назначать большее значение α в том случае, когда в модели наиболее прогностическим является именно последнее наблюдение. Если же α близко к 0, это означает практически полное доверие к прошлому прогнозу и игнорирование последнего наблюдения.Перед менеджером возникает проблема: как наилучшим образом подобрать значение α? В этом поможет средство Поиск решения. Чтобы найти оптимальное значение α (т.е. такое, при котором прогнозная кривая будет менее всего отклоняться от кривой значений временного ряда), выполните следующие действия. Выберите команду Сервис -> Поиск решения. В открывшемся диалоговом окне Поиск решения установите целевую ячейку G16 (см. лист «Экспо») и укажите, что ее значение должно быть минимальным. Укажите, что изменяемой ячейкой является ячейка В1. Введите ограничения В1 > 0 и B1 < 1 Щелкнув на кнопке Выполнить, получите результат, показанный на рис. 6. 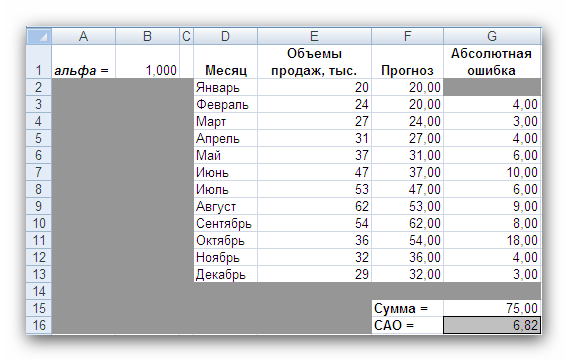 Рис. 6 Опять, как и в методе взвешенного скользящего среднего, наилучший прогноз будет получен, если назначить весь вес последнему наблюдению. Следовательно, оптимальное значение α равно 1, при этом среднее абсолютных отклонений равно 6,82 (ячейка G16). Метод экспоненциального сглаживания хорошо работает в ситуациях, когда интересующая нас переменная ведет себя стационарно, а ее отклонения от постоянного значения вызваны случайными факторами и не носят регулярного характера. Но этим методом, как и методами скользящего среднего не удастся спрогнозировать монотонно возрастающие или монотонно убывающие данные. Прогнозируемы значения будут всегда меньше или больше наблюдаемых, соответственно, а точность данных будет сравнима с точностью «наивного прогноза». Эти методы также не учитывают сезонных изменений показателя ряда. Если статистические данные монотонно изменяются или подвержены сезонным изменениям, необходимы специальные методы прогнозирования, которые будут рассмотрены ниже. Подбор кривой тренда. В качестве примера, воспользуемся данными объемов продаж из файла Продажи.xls. Вначале построим точечную диаграмму, отображающие реальные объемы продаж. Чтобы теперь построить по этим данным линию тренда, отражающую тенденцию в изменении объемов продаж, надо выполнить такие действия. Кликните на любой точке выбранного ряда данных. В результате будут выделены все точки ряда. Кликните правой кнопкой, и в появившемся меню выберите Добавить линию тренда. В диалоговом окне Линия тренда по умолчанию будет выбран линейный тип функции. Кликнете на кнопке ОК. После этого на графике появится прямая линия тренда (рис. 7). 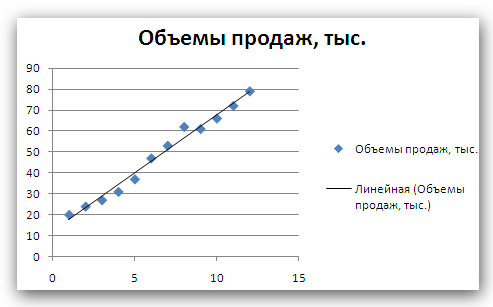 Рис. 7 Для того чтобы осуществить прогноз, нужно в диалоговом окне Линия тренда отметить интересующий интервал времени в пункте вперед на (или назад на). В меню Линия тренда можно также задать параметры подбираемой кривой. Например, он может быть экспоненциальной или полиномом заданной степени. В нашем случае кривой тренда является прямая линия с уравнением  . Коэффициенты  и  для этой кривой можно также найти с помощью надстройки Пакет Анализа, выбрав средство Регрессия.Метод Хольта — представляет собой развитие метода экспоненциального сглаживания, с учетом наличия тренда. Формулировка метода имеет вид  ,где  , .Метод Хольта позволяет прогнозировать на k периодов времени вперед. Метод, как видно, использует два параметра α и β, значения которых находятся в пределах от 0 до 1. Переменная L, указывает на долгосрочный уровень значений или базовое значение данных временного ряда. Переменная Т указывает на возможное возрастание или убывание значений за один период, т. е. на присутствие тренда. Рассмотрим работу этого метода на следующем примере. Светлана работает аналитиком в большой брокерской фирме. На основе имеющихся у нее квартальных отчетов компании Startup Airlines она хочет спрогнозировать доход этой компании в следующем квартале. Имеющиеся данные и диаграмма, построенная на их основе, находятся в файле Startup.xls (рис. 8). Видно, что данные имеют явный тренд (почти монотонно возрастают). Светлана хочет применить метод Хольта, чтобы спрогнозировать значение прибыли на одну акцию на тринадцатый квартал. Для этого необходимо задать начальные значения для L и Т. Есть несколько вариантов выбора: 1) L равно значению прибыли на одну акцию за первый квартал и T = 0; 2) L равно среднему значению прибыли на одну акцию за 12 кварталов и T равно среднему изменению за все 12 кварталов. Существуют и другие варианты начальных значений для L и Т, но Светлана выбрала первый вариант. Она решила воспользоваться средством Поиск решения, чтобы найти оптимальное значение параметров α и β, при которых значение среднего абсолютных ошибок в процентах было бы минимально. Для этого нужно выполнить такие действия. Выбрать команду Сервис -> Поиск решения. В открывшемся диалоговом окне Поиск решения задать ячейку F18 целевой и указать, что ее значение следует минимизировать. В поле Изменяя ячейки ввести диапазон ячеек В1:В2. Добавить ограничения В1:В2 > 0 и В1:В2 < 1. Кликнуть на кнопке Выполнить. Полученный прогноз показан на рис. 9, 10. Как видно, оптимальными оказались значения α = 0,59 и β = 0,42, при этом среднее абсолютных ошибок в процентах равно около 38%. 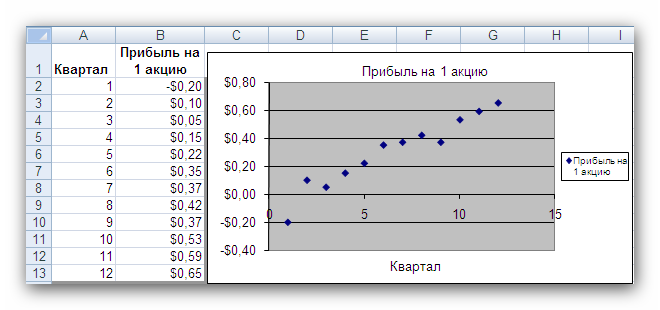 Рис. 8 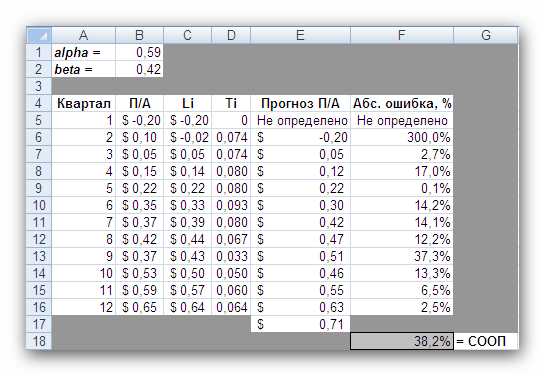 Рис. 9 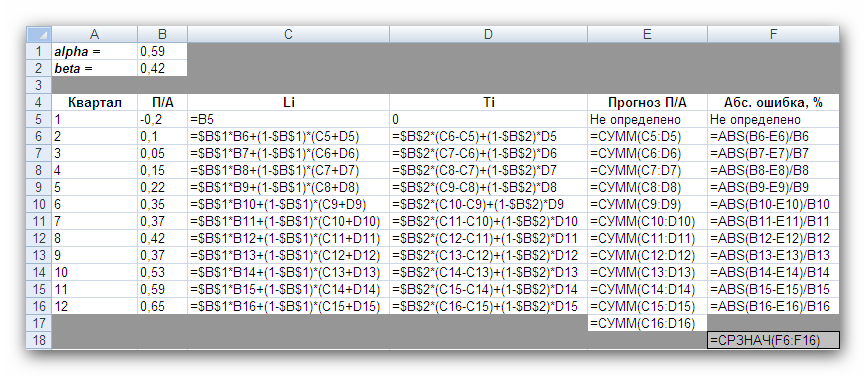 Рис. 10 Однако метод Хольта, как и рассмотренные ранее простейшие методы прогнозирования, не учитывает наличие во временном ряде сезонных изменений. Учет сезонных изменений. Спрос на значительное число товаров меняется в течение года. Например, если посмотреть на объемы продаж мороженого по месяцам, то можно увидеть в теплые месяцы (с июня по август в северном полушарии) более высокий уровень продаж, чем зимой, и так каждый год. Здесь сезонные колебания имеют период в 12 месяцев. Другой пример: анализируются еженедельные отчеты о количестве постояльцев, которые оставались на ночь в отеле, расположенном в бизнес-центре города. Предположительно можно сказать, что большое число клиентов ожидается в ночи на вторник, среду и четверг, меньше всего клиентов будет в ночи на субботу и воскресенье, и среднее число постояльцев ожидается в ночи на пятницу и понедельник. Такая структура данных, отображающая количество клиентов в разные дни недели, будет повторяться через каждые семь дней. Подобные циклические изменения показателя временного ряда носят название сезонных колебаний (хотя сезон, как мы видели, может продлиться и неделю и год). Процедура, которая позволяет сделать прогноз с учетом сезонных изменений, состоит из следующих этапов. На основе исходных данных определяется структура сезонных колебаний и период этих колебаний. Используя численный метод, описанный далее, из исходных данных исключают сезонную составляющую. На основе данных, из которых исключена сезонная составляющая, делается наилучший возможный прогноз. К полученному прогнозу добавляется сезонная составляющая. Проиллюстрируем этот подход на данных об объемах сбыта угля (измеряемого в тысячах тонн) в США на протяжении девяти лет. Пусть некто Фрэнк работает менеджером в компании Gillette Coal Mine, и ему необходимо спрогнозировать спрос на уголь на ближайшие два квартала. Он ввел данные по всей угольной отрасли в рабочую книгу Уголь.xls и построил по этим данным график (рис. 11). Определение структура и периода сезонных колебаний. Из графика на рис. 11 видно, что объемы продаж выше среднего уровня в первом и четвертом кварталах (зимнее время года) и ниже среднего во втором и третьем кварталах (весенне-летние месяцы). 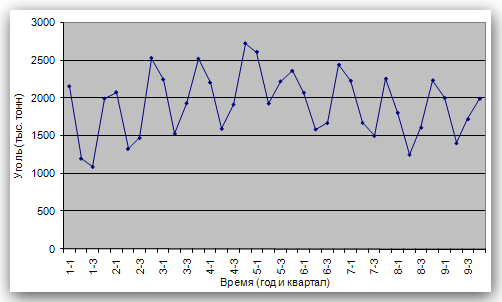 Рис. 11 Исключение сезонной составляющей. Сначала необходимо вычислить среднее значение всех отклонений за один период сезонных изменений. Чтобы исключить сезонную составляющую в пределах одного года, используются данные за четыре периода (квартала). А чтобы исключить сезонную составляющую из всего временного ряда, вычисляется последовательность скользящих средних по T узлам, где T — продолжительность сезонных колебаний. Для выполнения необходимых вычислений Фрэнк использовал столбцы С и D, как показано на рис. ниже. Столбец С содержит значения скользящего среднего по 4 узлам на основе данных, которые находятся в столбце В. Теперь надо назначить полученные значения скользящего среднего средним точкам последовательности данных, на основе которых эти значения были вычислены. Эта операция называется центрированием значений. Если T нечетное, то первое значение скользящего среднего (среднее значений от первой до T-й точки) надо присвоить (T + 1)/2 точке (например, если T = 7, то первое скользящее среднее будет назначено четвертой точке). Аналогично среднее значений от второй до (T + 1)-й точки центрируется в (T + 3)/2 точке и т. д. Центр n-го интервала находится в точке (T+(2n-1))/2. Если T четное, как в рассматриваемом случае, то задача несколько усложняется, поскольку здесь центральные (средние) точки расположены между точками, по которым вычислялось значение скользящего среднего. Поэтому центрированное значение для третьей точки вычисляется как среднее первого и второго значений скользящего среднего. Например, первое число в столбце D отцентрированных средних на рис. 12, слева равняется (1613 + 1594)/2 = 1603.
Рис. 12 На рис. 13 показаны графики исходных данных и отцентрированных средних. 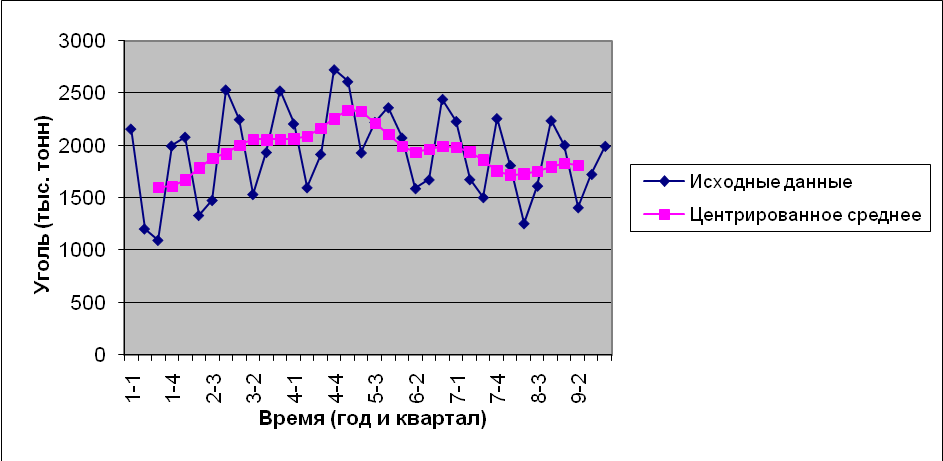 Рис. 13 Далее находим отношения значений точек данных к соответствующим значениям отцентрированных средних (рис. 14). Поскольку точкам в начале и конце последовательности данных нет соответствующих отцентрированных средних (см. первые и последние значения в столбце D), такое действие на эти точки не распространяется. Эти отношения показывают степень отклонения значений данных относительно типового уровня, определяемого отцентрированными средними. Заметим, что значения отношений для третьих кварталов меньше 1, а для четвертых — больше 1.
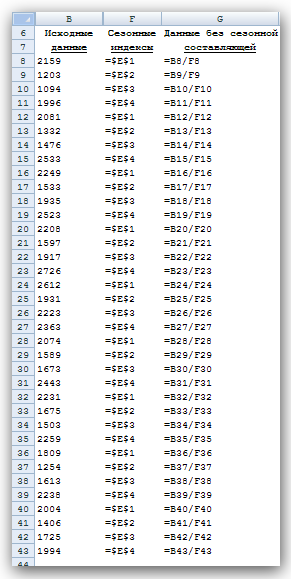
Рис. 14 Эти отношения являются основой для создания сезонных индексов. Для их вычисления группируются вычисленные отношения по кварталам, как показано на рис. 15 в столбцах G—О.  Рис. 15 Затем находятся средние значения отношений по каждому кварталу (столбец Е на рис. 15). Например, среднее всех отношений для первого квартала равно 1,108. Это значение является сезонным индексом первого квартала, на основе которого можно сделать вывод, что объем сбыта угля за первый квартал составляет в среднем около 110,8% относительного среднего годового объема сбыта. Сезонный индекс — это среднее отношение данных, относящихся к одному сезону (в данном случае сезоном является квартал), ко всем данным. Если сезонный индекс больше 1, значит, показатели этого сезона выше средних показателей за год, аналогично, если сезонный индекс ниже 1, то показатели сезона ниже средних показателей за год. Наконец, чтобы исключить из исходных данных сезонную составляющую, следует поделить значения исходных данных на соответствующий сезонный индекс. Результаты этой операции приведены в столбцах F и G (рис. 16). График данных, которые уже не содержат сезонной составляющей, представлен на рис. 17.
Рис. 16 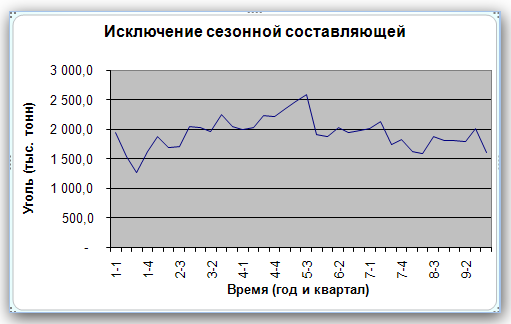 Рис. 17 Прогнозирование без сезонной составляющей. На основе данных, из которых исключена сезонная составляющая, строится прогноз. Для этого используется соответствующий метод, который учитывает характер поведения данных (например, данные имеют тренд или относительно постоянны). В этом примере прогноз строится с помощью простого экспоненциального сглаживания. Оптимальное значение параметра α находится с помощью средства Поиск решения. Графики прогноза и реальных данных с исключенной сезонной составляющей приведены на рис. 18. 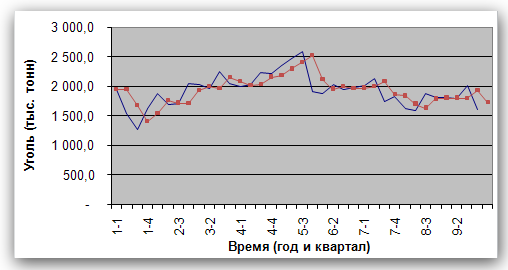 Рис. 18 Учет сезонной структуры. Теперь нужно учесть в полученном прогнозе (1726,5) сезонную составляющую. Для этого следует умножить 1726 на сезонный индекс первого квартала 1,108, в результате чего получим значение 1912. Аналогичная операция (умножение 1726 на сезонный индекс 0,784) даст прогноз на второй квартал, равный 1353. Результат добавления сезонной структуры к полученному прогнозу показан на рис. 19. 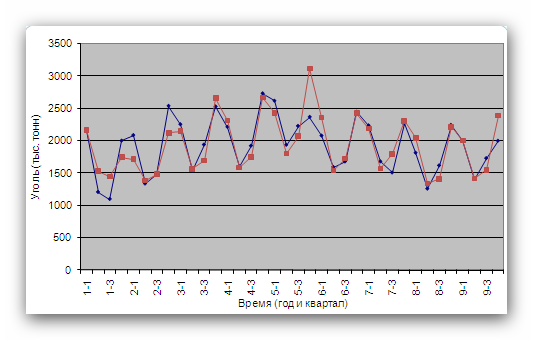 Рис. 19 Задания |
