
|
-7, -12
|
Вывод программы
|
a
|
5
|
208 0.998535 0.993793 0.0000214864 1
209 0.998582 0.993989 0.0000201452 1
210 0.998627 0.994180 0.0000188878 1
211 0.998670 0.994364 0.0000177089 1
212 0.998712 0.994543 0.0000166037 1
213 0.998753 0.994716 0.0000155674 1
214 0.998793 0.994884 0.0000145959 1
215 0.998831 0.995046 0.0000136850 1
216 0.998868 0.995203 0.0000128310 1
217 0.998904 0.995355 0.0000120303 1
218 0.998938 0.995502 0.0000112796 1
219 0.998972 0.995645 0.0000105758 1
220 0.999005 0.995783 0.0000099159 1
|
k*
|
220
|
Точка, в которой значение F(x1k,x2k,a) в первый раз стало < 10-5:
|
x1 =0.999005 x2 =0.995783 a=5
|

|
-7, -12
|
Вывод программы
|
a
|
15
|
154 0.999324 0.993838 0.0000299919 1
155 0.999356 0.994127 0.0000272480 1
156 0.999386 0.994402 0.0000247552 1
157 0.999415 0.994664 0.0000224904 1
158 0.999442 0.994914 0.0000204329 1
159 0.999468 0.995152 0.0000185636 1
160 0.999493 0.995379 0.0000168654 1
161 0.999517 0.995596 0.0000153225 1
162 0.999539 0.995802 0.0000139208 1
163 0.999561 0.995999 0.0000126474 1
164 0.999581 0.996186 0.0000114904 1
165 0.999601 0.996365 0.0000104393 1
166 0.999620 0.996535 0.0000094843 1
|
k*
|
166
|
Точка, в которой значение F(x1k,x2k,a) в первый раз стало < 10-5:
|
x1 =0.999620 x2 = 0.996535 a=15
|
3.2. Метод наискорейшего спуска

|
2, 2
|
Вывод программы
|
a
|
1
|
2 1.251209 1.429201 0.0816900746 22
3 1.174409 1.446876 0.0349935312 12
4 1.115322 1.189626 0.0162495525 18
5 1.079238 1.197914 0.0073782321 12
6 1.053185 1.085229 0.0034032157 20
7 1.036104 1.089178 0.0015489319 13
8 1.024315 1.038441 0.0007074678 18
9 1.016391 1.040282 0.0003209573 14
10 1.011021 1.017287 0.0001452296 21
11 1.007395 1.018133 0.0000655012 12
12 1.004967 1.007763 0.0000294979 21
13 1.003326 1.008147 0.0000132646 13
14 1.002248 1.003520 0.0000060181 20
|
k*
|
14
|
Точка, в которой значение F(x1k,x2k,a) в первый раз стало < 10-5:
|
x1 =1.002248 x2 =1.003520 a=1
|

|
2, 2
|
Вывод программы
|
a
|
5
|
1 1.269591 2.112371 0.6139061040 12
2 1.114979 1.108347 0.0842799955 20
3 1.028382 1.121683 0.0081381625 12
4 1.010776 1.009315 0.0007332883 17
5 1.002457 1.010618 0.0000626528 11
6 1.000989 1.000907 0.0000060383 18
|
k*
|
6
|
Точка, в которой значение F(x1k,x2k,a) в первый раз стало < 10-5:
|
x1 = 1.000989 x2 = 1.000907 a=5
|

|
2, 2
|
Вывод программы
|
a
|
15
|
1 1.125893 2.076009 0.8912046521 11
2 1.036806 1.018588 0.0234994841 20
3 1.002323 1.021494 0.0003646099 12
4 1.000998 1.000892 0.0000161688 19
5 1.000103 1.000950 0.0000007124 11
|
k*
|
5
|
Точка, в которой значение F(x1k,x2k,a) в первый раз стало < 10-5:
|
x1 =1.000103 x2 =1.000950 a=15
|

|
3, -2
|
Вывод программы
|
a
|
1
|
9 0.944005 0.863898 0.0038778499 12
10 0.953460 0.920495 0.0022961815 19
11 0.966554 0.918308 0.0013720508 13
12 0.972241 0.952173 0.0008184747 17
13 0.979950 0.950879 0.0004907979 13
14 0.983345 0.971132 0.0002947285 19
15 0.987925 0.970364 0.0001775242 13
16 0.989985 0.982600 0.0001067004 21
17 0.992730 0.982137 0.0000642458 13
18 0.993965 0.989490 0.0000387326 18
19 0.995613 0.989213 0.0000233761 14
20 0.996362 0.993660 0.0000140878 19
21 0.997354 0.993493 0.0000084956 13
|
k*
|
21
|
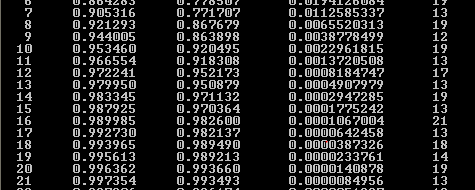
Точка, в которой значение F(x1k,x2k,a) в первый раз стало < 10-5:
|
x1 =0.997354 x2 = 0.993493 a=1
|

|
3, -2
|
Вывод программы
|
a
|
5
|
1 0.536494 -1.643440 4.8039764201 11
2 0.852764 0.846570 0.1226390555 18
3 0.961936 0.832704 0.0158222159 11
4 0.981136 0.979261 0.0020558819 19
5 0.994823 0.977468 0.0002829631 11
6 0.997411 0.997139 0.0000388449 17
7 0.999285 0.996892 0.0000053724 12
|
k*
|
7
|

Точка, в которой значение F(x1k,x2k,a) в первый раз стало < 10-5:
|
x1 = 0.999285 x2 = 0.996892 a=5
|

|
3, -2
|
Вывод программы
|
a
|
15
|
1 0.747824 -1.741938 6.2493154153 10
2 1.130588 0.841884 0.4461965082 15
3 0.984953 0.863459 0.0147754288 10
4 1.004202 0.995422 0.0004339016 19
5 0.999565 0.996099 0.0000120293 11
6 1.000133 0.999830 0.0000004540 18
|
k*
|
6
|
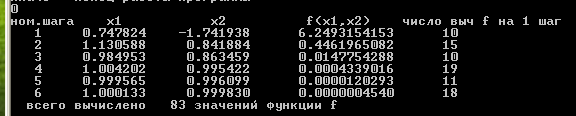
Точка, в которой значение F(x1k,x2k,a) в первый раз стало < 10-5:
|
x1 = 1.000133 x2 = 0.999830 a=15
|

|
6, 3
|
Вывод программы
|
a
|
1
|
5 1.152548 1.388933 0.0269391858 13
6 1.109182 1.185947 0.0138866868 20
7 1.077135 1.192793 0.0070108237 12
8 1.055783 1.092932 0.0035845831 19
9 1.038991 1.096523 0.0018099972 13
10 1.028449 1.046954 0.0009249878 18
11 1.019803 1.048792 0.0004694932 12
12 1.014482 1.023761 0.0002390443 19
13 1.010050 1.024703 0.0001212719 13
14 1.007358 1.012035 0.0000616198 22
15 1.005098 1.012516 0.0000312498 13
16 1.003740 1.006113 0.0000158951 20
17 1.002590 1.006357 0.0000080776 13
|
k*
|
17
|
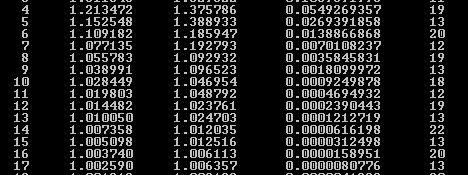
Точка, в которой значение F(x1k,x2k,a) в первый раз стало < 10-5:
|
x1 = 1.002590 x2 = 1.006357 a=1
|

|
6, 3
|
Вывод программы
|
a
|
5
|
10 1.077585 1.172525 0.0302260163 16
11 1.038227 1.171298 0.0160268207 12
12 1.040678 1.088698 0.0083059591 17
13 1.019535 1.088070 0.0042718757 11
14 1.020830 1.045049 0.0021781629 17
15 1.009887 1.044719 0.0011061668 12
16 1.010552 1.022717 0.0005589663 16
17 1.004975 1.022549 0.0002818596 12
18 1.005324 1.011462 0.0001423185 17
19 1.002507 1.011373 0.0000717854 12
20 1.002683 1.005768 0.0000361455 17
21 1.001261 1.005724 0.0000181905 12
22 1.001350 1.002900 0.0000091481 17
|
k*
|
22
|
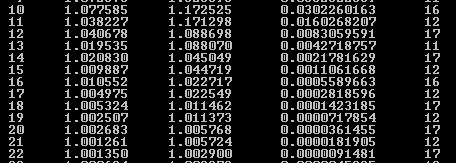
Точка, в которой значение F(x1k,x2k,a) в первый раз стало < 10-5:
|
x1 = 1.001350 x2 = 1.002900 a=5
|

|
6, 3
|
Вывод программы
|
a
|
15
|
1 1.300982 3.329231 4.0375620792 9
2 0.947792 1.072570 0.0712515800 19
3 1.007095 1.063289 0.0031608255 11
4 0.997734 1.003144 0.0001358533 19
5 1.000306 1.002744 0.0000059494 11
|
k*
|
5
|
Точка, в которой значение F(x1k,x2k,a) в первый раз стало < 10-5:
|
x1 = 1.000306 x2 = 1.002744 a=15
|

|
4, -8
|
Вывод программы
|
a
|
1
|
10 1.028795 1.053570 0.0008526828 18
11 1.021921 1.054429 0.0005826804 14
12 1.019671 1.036428 0.0003978287 18
13 1.014932 1.037021 0.0002710418 13
14 1.013417 1.024794 0.0001849539 19
15 1.010174 1.025196 0.0001260223 13
16 1.009141 1.016856 0.0000858365 19
17 1.006922 1.017131 0.0000584060 12
18 1.006225 1.011470 0.0000397904 18
19 1.004712 1.011657 0.0000270892 13
20 1.004241 1.007812 0.0000184630 19
21 1.003210 1.007938 0.0000125773 13
22 1.002886 1.005309 0.0000085538 21
|
k*
|
22
|

Точка, в которой значение F(x1k,x2k,a) в первый раз стало < 10-5:
|
x1 = 1.002886 x2 =1.005309 a=1
|

|
4, -8
|
Вывод программы
|
a
|
5
|
1 0.202678 -7.559731 60.9509116590 11
2 1.267572 1.378281 0.4101655597 18
3 1.093663 1.399006 0.0850353286 12
4 1.053544 1.066626 0.0162125639 18
5 1.016389 1.071110 0.0027918257 10
6 1.009187 1.011171 0.0004750593 18
7 1.002743 1.011945 0.0000792448 12
8 1.001537 1.001867 0.0000132723 19
9 1.000458 1.001996 0.0000022155 12
|
k*
|
9
|
Точка, в которой значение F(x1k,x2k,a) в первый раз стало < 10-5:
|
x1 = 1.000458 x2 =1.001996 a=5
|

|
4, -8
|
Вывод программы
|
a
|
15
|
1 0.457875 -7.641304 66.0459607050 9
2 1.477164 0.850475 5.1882805686 18
3 0.990390 0.908914 0.0065633062 9
4 0.992139 0.987099 0.0009344971 18
5 0.998616 0.986955 0.0001343954 12
6 0.998862 0.998119 0.0000195773 18
7 0.999798 0.998099 0.0000028547 11
|
k*
|
7
|
Точка, в которой значение F(x1k,x2k,a) в первый раз стало < 10-5:
|
x1 = 0.999798 x2 =0.998099 a=15
|

|
6, 10
|
Вывод программы
|
a
|
1
|
65 1.006152 1.015687 0.0000490346 13
66 1.006475 1.013822 0.0000426113 15
67 1.005345 1.013627 0.0000370260 13
68 1.005625 1.012004 0.0000321646 14
69 1.004642 1.011834 0.0000279395 14
70 1.004886 1.010424 0.0000242678 15
71 1.004031 1.010276 0.0000210773 13
72 1.004243 1.009050 0.0000183035 16
73 1.003500 1.008921 0.0000158938 14
74 1.003685 1.007856 0.0000137993 14
75 1.003038 1.007744 0.0000119802 12
76 1.003199 1.006818 0.0000104000 14
77 1.002638 1.006721 0.0000090279 12
|
k*
|
77
|
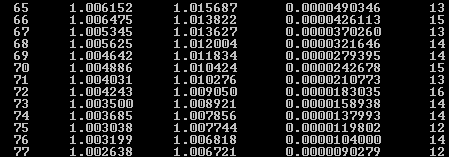
Точка, в которой значение F(x1k,x2k,a) в первый раз стало < 10-5:
|
x1 = 1.002638 x2 =1.006721 a=1
|

|
6, 10
|
Вывод программы
|
a
|
5
|
35 1.021237 1.097203 0.0052011979 12
36 1.024554 1.058706 0.0030954918 18
37 1.012562 1.057672 0.0018381354 10
38 1.014542 1.034609 0.0010855612 16
39 1.007390 1.033995 0.0006401879 11
40 1.008569 1.020365 0.0003770595 16
41 1.004341 1.020000 0.0002218813 12
42 1.005042 1.011982 0.0001306083 17
43 1.002552 1.011765 0.0000768445 11
44 1.002966 1.007046 0.0000451987 18
45 1.001500 1.006917 0.0000265773 11
46 1.001744 1.004146 0.0000156398 17
47 1.000882 1.004070 0.0000092026 11
|
k*
|
47
|
Точка, в которой значение F(x1k,x2k,a) в первый раз стало < 10-5:
|
x1 =1.000882 x2 = 1.004070 a=5
|

|
6, 10
|
Вывод программы
|
a
|
15
|
1 2.436143 10.239432 49.4675224110 8
2 1.197172 0.861616 0.9098878407 20
3 0.987860 0.889271 0.0097095700 11
4 1.001821 0.998981 0.0000714982 19
5 0.999914 0.999224 0.0000004758 11
|
k*
|
5
|
Точка, в которой значение F(x1k,x2k,a) в первый раз стало < 10-5:
|
x1 =0.999914 x2 =0.999224 a=15
|

|
-7, -12
|
Вывод программы
|
a
|
1
|
35 0.991549 0.978769 0.0000907797 13
36 0.991332 0.982261 0.0000753581 17
37 0.992982 0.982364 0.0000625721 14
38 0.992801 0.985254 0.0000519849 18
39 0.994167 0.985339 0.0000431968 13
40 0.994018 0.987739 0.0000359002 17
41 0.995151 0.987810 0.0000298412 13
42 0.995027 0.989802 0.0000248110 17
43 0.995967 0.989861 0.0000206313 13
44 0.995864 0.991516 0.0000171585 17
45 0.996645 0.991565 0.0000142718 12
46 0.996560 0.992942 0.0000118697 18
47 0.997209 0.992983 0.0000098727 13
|
k*
|
47
|
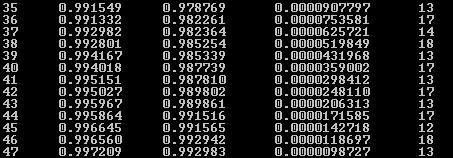
Точка, в которой значение F(x1k,x2k,a) в первый раз стало < 10-5:
|
x1 =0.997209 x2 =0.992983 a=1
|

|
-7, -12
|
Вывод программы
|
a
|
5
|
9 0.970393 0.863093 0.0105561190 12
10 0.966813 0.926251 0.0055787506 16
11 0.984177 0.927235 0.0029632304 11
12 0.982315 0.960483 0.0015836744 16
13 0.991497 0.960997 0.0008485444 11
14 0.990499 0.978677 0.0004571618 15
15 0.995403 0.978954 0.0002466428 10
16 0.994876 0.988502 0.0001329244 15
17 0.997518 0.988648 0.0000716865 13
18 0.997236 0.993797 0.0000386630 15
19 0.998660 0.993875 0.0000208603 12
20 0.998510 0.996662 0.0000112246 16
21 0.999278 0.996703 0.0000060406 12
|
k*
|
21
|

Точка, в которой значение F(x1k,x2k,a) в первый раз стало < 10-5:
|
x1 = 0.999278 x2 = 0.996703 a=5
|

|
-7, -12
|
Вывод программы
|
a
|
15
|
1 0.385655 -11.537449 142.2280635100 9
2 0.592489 0.458612 2.5025549242 18
3 0.944008 0.452553 0.2393950207 10
4 0.956974 0.934124 0.0281048716 18
5 0.992893 0.933157 0.0035327755 9
6 0.995167 0.993322 0.0003591700 18
7 0.999268 0.993167 0.0000368722 11
8 0.999559 0.999455 0.0000030364 18
|
k*
|
8
|
Точка, в которой значение F(x1k,x2k,a) в первый раз стало < 10-5:
|
x1 =0.999559 x2 =0.999455 a=15
|
3. Расчет скорости сходимости и порядка сходимости.
Метод с дроблением шага.

|
2, 2
|
a
|
1
|
h
|
0.03
|
№
|
x1
|
x2
|
F(x1,x2)
|
F(k+1)/F(k) Скорость сходимости
|
ln||x-1||
|
ln||x_{k+1} -1||/ln||x{k}-1|| Порядок сходимости
|
527
|
1,003284
|
1,007937
|
0,0000126295
|
0,9796112277
|
-4,757207197
|
1,002174248
|
528
|
1,003251
|
1,007855
|
0,000012372
|
0,9796071775
|
-4,767550546
|
1,002155667
|
529
|
1,003217
|
1,007775
|
0,0000121197
|
0,9796117066
|
-4,777827798
|
1,002163756
|
530
|
1,003184
|
1,007695
|
0,0000118726
|
0,9796085104
|
-4,788165854
|
1,002148535
|
531
|
1,003152
|
1,007616
|
0,0000116305
|
0,979605348
|
-4,798453395
|
1,002142608
|
532
|
1,00312
|
1,007538
|
0,0000113933
|
0,9796108239
|
-4,808734602
|
1,00213644
|
533
|
1,003088
|
1,007461
|
0,000011161
|
0,979607562
|
-4,819008175
|
1,002154015
|
534
|
1,003056
|
1,007384
|
0,0000109334
|
0,9796037829
|
-4,829388391
|
1,002137726
|
535
|
1,003025
|
1,007308
|
0,0000107104
|
0,979599268
|
-4,8397123
|
1,002131028
|
536
|
1,002994
|
1,007233
|
0,0000104919
|
0,979603313
|
-4,850025865
|
1,002124067
|
537
|
1,002963
|
1,007159
|
0,0000102779
|
0,979606729
|
-4,860327646
|
1,002116835
|
538
|
1,002932
|
1,007086
|
0,0000100683
|
0,9795993365
|
-4,870616159
|
1,002123979
|
539
|
1,002902
|
1,007013
|
0,0000098629
|
|
-4,880961244
|
|
Метод с дроблением шага сходится с порядком 1. В соотношении |𝐹(𝑥𝑘+1) − 𝐹(𝑥∗)| ≤ 0,98|𝐹(𝑥𝑘) − 𝐹(𝑥∗)| значение q близко к 1. Сходимость линейная. Полученные результаты соответствуют теоретическим сведениям.

|
6, 10
|
a
|
5
|
h
|
0.03
|
№
|
x1
|
x2
|
F(x1,x2)
|
F(k+1)/F(k) Скорость сходимости
|
ln||x-1||
|
ln||x_{k+1} -1||/ln||x{k}-1|| Порядок сходимости
|
283
|
1,001452
|
1,006148
|
0,0000210486
|
0,9377393271
|
-5,064489329
|
1,006363821
|
284
|
1,001406
|
1,005953
|
0,0000197381
|
0,937734635
|
-5,096718831
|
1,006300783
|
285
|
1,001361
|
1,005765
|
0,0000185091
|
0,9377333312
|
-5,128832153
|
1,006287962
|
286
|
1,001318
|
1,005582
|
0,0000173566
|
0,9377297397
|
-5,161082054
|
1,006203091
|
287
|
1,001277
|
1,005406
|
0,0000162758
|
0,9377296354
|
-5,193096717
|
1,006194477
|
288
|
1,001236
|
1,005235
|
0,0000152623
|
0,9377289137
|
-5,225265238
|
1,006165192
|
289
|
1,001197
|
1,005069
|
0,0000143119
|
0,9377231535
|
-5,257480002
|
1,006102393
|
290
|
1,001159
|
1,004909
|
0,0000134206
|
0,9377226055
|
-5,289563211
|
1,006106781
|
291
|
1,001122
|
1,004753
|
0,0000125848
|
0,9377185176
|
-5,321865414
|
1,006021921
|
292
|
1,001087
|
1,004603
|
0,000011801
|
0,9377171426
|
-5,353913264
|
1,006025231
|
293
|
1,001052
|
1,004457
|
0,000011066
|
0,9377191397
|
-5,386171829
|
1,005965704
|
294
|
1,001019
|
1,004316
|
0,0000103768
|
0,9377168299
|
-5,418304134
|
1,005949938
|
295
|
1,000987
|
1,004179
|
0,0000097305
|
|
-5,450542708
|
|
Метод с дроблением шага сходится с порядком 1. В соотношении |𝐹(𝑥𝑘+1) − 𝐹(𝑥∗)| ≤ 0,94|𝐹(𝑥𝑘) − 𝐹(𝑥∗)| значение q близко к 1. Сходимость линейная. Полученные результаты соответствуют теоретическим сведениям.
Метод наискорейшего спуска.

|
3, -2
|
a
|
1
|
h
|
0.03
|
№
|
x1
|
x2
|
F(x1,x2)
|
F(k+1)/F(k) Скорость сходимости
|
ln||x-1||
|
ln||x_{k+1} -1||/ln||x{k}-1|| Порядок сходимости
|
9
|
0,944005
|
0,863898
|
0,0038778499
|
0,5921274828
|
-1,916162615
|
1,244471033
|
10
|
0,95346
|
0,920495
|
0,0022961815
|
0,5975358655
|
-2,38460887
|
1,017909022
|
11
|
0,966554
|
0,918308
|
0,0013720508
|
0,5965338164
|
-2,427314882
|
1,192675792
|
12
|
0,972241
|
0,952173
|
0,0008184747
|
0,5996494455
|
-2,8949997
|
1,014307078
|
13
|
0,97995
|
0,950879
|
0,0004907979
|
0,6005088856
|
-2,936418687
|
1,158336078
|
14
|
0,983345
|
0,971132
|
0,0002947285
|
0,6023312981
|
-3,401359706
|
1,011939861
|
15
|
0,987925
|
0,970364
|
0,0001775242
|
0,6010470685
|
-3,441971468
|
1,13545749
|
16
|
0,989985
|
0,9826
|
0,0001067004
|
0,6021139565
|
-3,908212283
|
1,01028019
|
17
|
0,99273
|
0,982137
|
0,0000642458
|
0,6028814335
|
-3,948389448
|
1,117656417
|
18
|
0,993965
|
0,98949
|
0,0000387326
|
0,6035251958
|
-4,412942805
|
1,009050387
|
19
|
0,995613
|
0,989213
|
0,0000233761
|
0,6026582706
|
-4,452881646
|
1,104579787
|
20
|
0,996362
|
0,99366
|
0,0000140878
|
0,6030466077
|
-4,918563059
|
1,008091936
|
21
|
0,997354
|
0,993493
|
0,0000084956
|
|
-4,958363758
|
|
У метода наискорейшего спуска значение порядка сходимости близко к единице, что соответствует теории (порядок сходимости метода наискорейшего спуска 1). При запусках программы выполнялось соотношение |𝐹(𝑥𝑘+1) − 𝐹(𝑥∗)| ≤ 0.6|𝐹(𝑥𝑘) − 𝐹(𝑥∗)| , метод сходится с линейной скоростью.

|
6, 3
|
a
|
1
|
h
|
0.03
|
№
|
x1
|
x2
|
F(x1,x2)
|
F(k+1)/F(k) Скорость сходимости
|
ln||x-1||
|
ln||x_{k+1} -1||/ln||x{k}-1|| Порядок сходимости
|
5
|
1,152548
|
1,388933
|
0,0269391858
|
0,5154827953
|
-0,8728013252
|
1,757769772
|
6
|
1,109182
|
1,185947
|
0,0138866868
|
0,5048593521
|
-1,534183786
|
1,024581525
|
7
|
1,077135
|
1,192793
|
0,0070108237
|
0,5112927173
|
-1,571896362
|
1,413599485
|
8
|
1,055783
|
1,092932
|
0,0035845831
|
0,5049393889
|
-2,222031889
|
1,018165005
|
9
|
1,038991
|
1,096523
|
0,0018099972
|
0,511043774
|
-2,262395109
|
1,282817331
|
10
|
1,028449
|
1,046954
|
0,0009249878
|
0,5075669106
|
-2,902239655
|
1,014370249
|
11
|
1,019803
|
1,048792
|
0,0004694932
|
0,5091539132
|
-2,943945561
|
1,216655276
|
12
|
1,014482
|
1,023761
|
0,0002390443
|
0,5073197729
|
-3,581766899
|
1,011860883
|
13
|
1,01005
|
1,024703
|
0,0001212719
|
0,5081127615
|
-3,624249818
|
1,175732867
|
14
|
1,007358
|
1,012035
|
0,0000616198
|
0,5071389391
|
-4,26114963
|
1,010055392
|
15
|
1,005098
|
1,012516
|
0,0000312498
|
0,5086464553
|
-4,303997161
|
1,147389418
|
16
|
1,00374
|
1,006113
|
0,0000158951
|
0,5081817667
|
-4,938360799
|
1,008717568
|
17
|
1,00259
|
1,006357
|
0,0000080776
|
|
-4,981411295
|
|
У метода наискорейшего спуска значение порядка сходимости близко к единице, что соответствует теории (порядок сходимости метода наискорейшего спуска 1). При запусках программы выполнялось соотношение |𝐹(𝑥𝑘+1) − 𝐹(𝑥∗)| ≤ 0.51|𝐹(𝑥𝑘) − 𝐹(𝑥∗)|, метод сходится с линейной скоростью.
Сводная таблица результатов работы программы для оценки эффективности методов и объяснение полученных результатов.
(В 3м и 4м столбцах указано, количество шагов k*, которое прошёл соответствующий алгоритм, чтобы добиться минимизации с точностью  ). ).

|
a
|
k* для метода с дроблением шага
|
k* для метода наискорейшего спуска
|
2, 2
|
1
|
539
|
14
|
5
|
180
|
6
|
15
|
121
|
5
|
3, -2
|
1
|
473
|
21
|
5
|
187
|
7
|
15
|
138
|
6
|
6, 3
|
1
|
536
|
17
|
5
|
199
|
22
|
15
|
139
|
5
|
4, -8
|
1
|
499
|
22
|
5
|
212
|
9
|
15
|
159
|
7
|
6, 10
|
1
|
1049
|
77
|
5
|
295
|
47
|
15
|
175
|
5
|
-7, -12
|
1
|
507
|
47
|
5
|
220
|
21
|
15
|
166
|
8
|
Объяснение полученных результатов.
Метод наискорейшего спуска
|
Метод дробления шага.
|
сходится гораздо быстрее метода дробления шага
вычисляет оптимальный шаг на каждом шаге задачи оптимизации
|
|
В обоих методах их скорость зависит от a: чем больше a, тем меньше шагов должен пройти алгоритм, чтобы достигнуть заданную точность.
Также наблюдается снижение скорости при отдалении начальной точки от точки минимума. Особенно это заметно у метода наискорейшего спуска.
Вывод.
Минимизирована функция F(x1,x2,a) = (x2 - x12)2 + a(x1 - 1)2 с точностью до 10-5 ( abs ( F(x1k,x2k,a) - F(x1*,x2*,a) ) < 10-5 ) градиентными методами - методом с дроблением шага и методом наискорейшего спуска.
Было установлено, что и тот и другой метод сходятся с линейной скоростью. Также выяснилось, что метод наискорейшего спуска сходится гораздо быстрее метода с дроблением шага. А ещё была установлена зависимость от параметра a в обоих методах: чем он больше, тем меньше шагов необходимо для минимизации. Довольно четко прослеживается в методе наискорейшего спуска снижение скорости при отдалении начальной точки от точки минимума. В методе с дроблением шага это тоже прослеживается, но не так выраженно. |
 Скачать 377.08 Kb.
Скачать 377.08 Kb.








 ).
).
