реферат пз-10. Методы и модели теории систем
 Скачать 53.16 Kb. Скачать 53.16 Kb.
|
2.МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ПЕРМСКИЙ ИНСТИТУТ (ФИЛИАЛ) федерального государственного бюджетного образовательного учреждения высшего образования «Российский экономический университет им. Г.В. Плеханова» Учётно-финансовый факультет Реферат по дисциплине «теория систем и системный анализ» на тему «Методы и модели теории систем» Выполнил – студент Ⅰ курса очной формы обучения учетно-финансового факультета, группы ПР-12 Ширинкин Данил Владимирович Руководитель – Ильин Вадим Владимирович Оценка_____________________________________ Дата_______________________________________ Подпись____________________________________ Пермь 2020 Содержание Введение 3 1.Определение понятия модель и моделирование………………….4 2.Назначение моделей. Классификация моделей…………………... 8 3.Уровни моделирования 13 Заключение……………………………………………………………………….15 Приложения………………………………………………………………………..16 Список литературы……………………………………………………………….17 Введение В поисках методов моделирования сложных систем и проблемных ситуаций исследователи обращались к различным разделам математики, предлагали новые, искали приемы и методы постановки задач, организации процесса коллективного принятия решений по разработке и совершенствованию сложных систем. Чтобы облегчить выбор методов в реальных условиях, необходимо разделить их на группы (классы) и разработать рекомендации по их использованию при отображении систем различных классов. Одной из проблем, с которой сталкиваются почти всегда при проведении системного анализа, является проблема эксперимента в системе или над системой. Очень редко это разрешено моральными законами или законами безопасности, но сплошь и рядом связано с материальными затратами и значительными потерями информации. 1.Определение понятия модель и моделирование Первоначально моделью называли некое вспомогательное средство, объект, который в определённой ситуации заменял другой объект. При этом далеко не сразу была понята универсальность законов природы, всеобщность моделирования, т.е. не просто возможность, но и необходимость представлять любые наши знания в виде моделей. Например, древние философы считали невозможным моделирование естественных процессов, так как, по их представлениям, природные и искусственные процессы подчинялись различным закономерностям. Они полагали, что отобразить природу можно только с помощью логики, методов рассуждений, споров, т.е., по современной терминологии, языковых (дескриптивных) моделей. Через несколько столетий девизом английского Королевского научного общества стал лозунг «Ничего словами!», который явился кратчайшим изложением принципов естествознания: признавались только выводы, подкреплённые экспериментально или математическими выкладками. В английском языке до сих пор в понятие «наука» не входят области знания, которым в русском языке соответствует термин «гуманитарные науки», – они отнесены к категории «искусств». В результате очень долго понятие «модель» относилось только к материальным объектам специального типа, например манекен (модель человеческой фигуры), гидродинамическая уменьшенная модель плотины, модели судов и самолетов, чучела (модели животных) и т.п. Осмысливание основных особенностей таких моделей привело к разработке многочисленных определений, типичным призером которых служит следующее: моделью называется некий объект-заместитель, который в определённых условиях может заменять объект-оригинал, воспроизводя интересующие нас свойства и характеристики оригинала, причём имеет существенные преимущества удобства (наглядность, обозримость, доступность испытаний, лёгкость оперирования с ним и пр.). Затем были осознаны модельные свойства чертежей, рисунков, карт – реальных объектов искусственного происхождения, воплощающих абстракцию довольно высокого уровня. Следующий шаг заключался в признании того, что моделями могут служить не только реальные объекты, но и абстрактные, идеальные построения. Типичным примером служат математические модели. В результате деятельности математиков, логиков и философов, занимавшихся исследованием оснований математики, была создана теория моделей. В ней модель определяется как результат отображения одной абстрактной математической структуры на другую, также абстрактную, либо как результат интерпретации первой модели в терминах и образах второй. В XX в. понятие модели становится всё более общим, охватывающим и реальные, и идеальные модели. При этом понятие абстрактной модели вышло за пределы математических моделей, стало относиться к любым знаниям и представлениям о мире. Следует отметить, что споры вокруг такого широкого толкования понятия модели продолжаются и поныне. Рассмотрим аргументы, фигурирующие в таких спорах. Стоит ли понятие абстрактной модели распространять на такие формы научных знаний, как законы, гипотезы, теории? Сторонники положительного ответа на этот вопрос отмечают, что психологический барьер неприятия объясняется тем, что понятия гипотезы, закономерности, теории сформировались и установились в языке науки и философии значительно раньше, чем понятие модели. Эти понятия, будучи исторически первыми, воспринимаются и как логически первичные, причём в этой схеме модели отводится роль лишь вспомогательного средства. Однако при этом содержание понятия модели неоправданно сужается. Модели могут быть качественно различными, они образуют иерархию, в которой модель более высокого уровня (например, теория) содержит модели нижних уровней (скажем, гипотезы) как свои части, элементы. Другой вопрос, часто возникающий в спорах: не означает ли такое широкое толкование модели, что это понятие становится применимым ко всему и, следовательно, логически пустым? Этот вопрос даёт возможность обсудить некоторые особенности моделей. Во-первых, ещё раз отметим иерархичность моделей, поэтому применительно к разным объектам понятие модели может иметь разное содержание. Во-вторых, тот факт, что любой объект может быть использован как модель, вовсе не означает, что он не может быть ничем иным. Например, ботинок также может являться моделью его владельца (скажем, по запаху ботинка сыскная собака отыщет преследуемого; по состоянию ботинка можно судить о некоторых особенностях сложения и даже чертах характера его хозяина), но это не лишает смысла ни понятие «обувь», ни понятие «модель». В-третьих, самые общие понятия совсем не являются логически пустыми: материя, движение, энергия, организация, система, модель. В широком смысле под моделированием следует понимать процесс адекватного отображения с помощью модели наиболее существенных сторон исследуемого объекта или явления с точностью, которая необходима для практических нужд. В общем случае моделированием можно назвать также особую форму опосредствования, основой которого является формализованный подход к исследованию сложной системы. Теоретической базой моделирования является теория подобия. Подобие – это взаимно однозначное соответствие между двумя объектами, при котором известны функции перехода от параметров одного объекта к параметрам другого, а математические описания этих объектов могут быть преобразованы в тождественные. Теория подобия даёт возможность установить наличие подобия или позволяет разработать способ его получения. Таким образом, моделирование – это процесс представления объекта исследования адекватной (подобной) ему моделью и проведения экспериментов с моделью для получения информации об объекте исследования. При моделировании модель выступает и как средство, и как объект исследований, находящийся в отношении подобия к моделируемому объекту. Иными словами, модель – это физическая или информационная система, представляющая собой объект исследования адекватно целям исследования. 2.Назначение моделей. Классификация моделей Всякий процесс труда есть деятельность, направленная на достижение определённой цели. Целевой характер имеет любая деятельность человека, она всегда целесообразна, целенаправленна. Важнейшим организующим элементом деятельности является цель – образ желаемого будущего, т.е. модель состояния, на реализацию которого направлена деятельность. Однако роль моделирования этим не ограничивается. Системность деятельности проявляется в том, что она осуществляется по определённому плану, или, как чаще говорят, по алгоритму. То есть алгоритм – образ будущей деятельности, её модель. В алгоритме моделируются все возможные ситуации, в зависимости от различных промежуточных значений параметров; возможные шаги деятельности не выполняются реально, а проигрываются на модели. Моделирование возникает в таких сферах человеческой деятельности, как познание, общение, практическая деятельность. Человека (субъекта моделирования) могут интересовать: внешний вид, структура, поведение объекта моделирования. Цели и задачи моделирования влияют на выбор одного из этих трёх аспектов. Каждый аспект моделирования раскрывается через совокупность свойств. Так, описание внешнего вида объекта сводится к перечислению его признаков. В языке эти признаки часто выражаются прилагательными: красивый, жёлтый, круглый, длинный и т.п. Описание структуры обычно сводится к перечислению составных элементов объекта и указанию связи между ними. В языке эти элементы и связи часто выражаются именами существительными: электрон, протон, нейтрон, сила притяжения, энергетический уровень (при описании атома). Некоторые свойства можно охарактеризовать величинами, принимающими числовые значения. Например, единицами массы, длины, мощности и пр. В этом случае они называются параметрами. Как правило, моделирование внешнего вида объекта необходимо для идентификации (узнавания) объекта (создание фоторобота преступника), долговременного хранения (фотография, портрет). Моделирование структуры объекта необходимо для её наглядного представления, изучения свойств объекта, выявления значимых связей, изучения стабильности объекта и пр. Поведением объекта назовем изменения, происходящие с ним с течением времени. Моделирование поведения необходимо для: прогнозирования, установления связей с другими объектами, управления, конструирования технических устройств и пр. Множественность моделей одного объекта обусловлена в частности тем, что для разных целей требуется строить (использовать) разные модели. Одним из оснований классификации моделей может быть соотнесение типов моделей с типами целей. Например, модели можно разделить на познавательные и прагматические. Познавательные модели являются формой организации и представления знаний, средством соединения новых знаний с имеющимися. Поэтому при обнаружении расхождения между моделью и реальностью встаёт задача устранения этого расхождения с помощью изменения модели путём приближения модели к реальности. Прагматические модели являются средством управления, средством организации практических действий, способом представления образцово правильных действий или их результата. Поэтому при обнаружении расхождения между моделью и реальностью встает задача устранения этого расхождения с помощью изменения реальности так, чтобы приблизить её к модели. Таким образом, прагматические модели носят нормативный характер, играют роль стандарта, образца, под которые «подгоняются» как сама деятельность, так и её результат. Примерами прагматических моделей могут служить планы, программы действий, уставы организаций, кодексы законов, алгоритмы, рабочие чертежи и шаблоны, параметры отбора, технологические допуски, экзаменационные требования и т.п. Различают физические и абстрактные модели. Физические модели образуются из совокупности материальных объектов. Для их построения используются различные физические свойства объектов, причём природа применяемых в модели материальных элементов не обязательно та же, что и в исследуемом объекте. Примером физической модели является макет. Информационная (абстрактная) модель – это описание объекта исследований на каком-либо языке. Абстрактность модели проявляется в том, что её компонентами являются понятия, а не физические элементы (например, словесные описания, чертежи, схемы, графики, таблицы, алгоритмы или программы, математические описания). Информационные модели описывают поведение объекта-оригинала, но не копируют его. Информационная модель – это целенаправленно отобранная информация об объекте, которая отражает наиболее существенные для исследователя свойства этого объекта. Среди информационных (абстрактных) моделей различают: – дескриптивные, наглядные и смешанные; – гносеологические, инфологические, кибернетические, сенсуальные (чувственные), концептуальные, математические. Гносеологические модели направлены на изучение объективных законов природы (например, модели солнечной системы, биосферы, мирового океана, катастрофических явлений природы). Сенсуальные модели – модели каких-то чувств, эмоций, либо модели, оказывающие воздействие на чувства человека (например, музыка, живопись, поэзия). Концептуальная модель – это абстрактная модель, выявляющая причинно-следственные связи, присущие исследуемому объекту и существенные в рамках определённого исследования. Основное назначение концептуальной модели – выявление набора причинно-следственных связей, учёт которых необходим для получения требуемых результатов. Один и тот же объект может представляться различными концептуальными моделями, которые строятся в зависимости от цели исследования. Так, одна концептуальная модель может отображать временные аспекты функционирования системы, иная – влияние отказов на работоспособность системы. Математическая модель – абстрактная модель, представленная на языке математических отношений. Она имеет форму функциональных зависимостей между параметрами, учитываемыми соответствующей концептуальной моделью. Эти зависимости конкретизируют причинно-следственные связи, выявленные в концептуальной модели, и характеризуют их количественно. Таким образом, модель – это специальный объект, в некоторых отношениях замещающий оригинал. Принципиально не существует модели, которая была бы полным эквивалентом оригинала. Любая модель отражает лишь некоторые стороны оригинала. Поэтому с целью получения больших зияний об оригинале приходится пользоваться совокупностью моделей. 3.Уровни моделирования В зависимости от степени детализации описания сложных систем и их элементов можно выделить три основных уровня моделирования: 1. Уровень структурного или имитационного моделирования сложных систем с использованием их алгоритмических моделей (моделирующих алгоритмов) и применением специализированных языков моделирования, теорий множеств, алгоритмов, формальных грамматик, графов, массового обслуживания, статистического моделирования. 2. Уровень логического моделирования элементов и функциональных подсистем сложных систем, модели которых представляются в виде уравнений непосредственных связей (логических уравнений) и строятся с применением аппарата двухзначной или многозначной алгебры логики. 3. Уровень количественного моделирования (анализа) принципиальных схем элементов сложных систем, модели которых представляются в виде систем нелинейных алгебраических, или интегро-дифференциальных уравнений и исследуются с применением методов функционального анализа, теории дифференциальных уравнений, математической статистики. Совокупность моделей объекта на структурном, логическом и количественном уровнях моделирования представляет собой иерархическую систему, раскрывающую взаимосвязь различных сторон описания объекта и обеспечивающую системную связность его элементов и свойств на всех стадиях процесса проектирования. При переходе на более высокий уровень абстрагирования осуществляется свёртка данных о моделируемом объекте, при переходе к более детальному уровню описания – развёртка этих данных. Рассмотрим этот вопрос более подробно. На структурном уровне моделируется состав элементов объекта на низшем уровне структурирования. К структурным относятся бинарные отношения иерархической подчинённости, отношения порядка, смежности, сопряжённости, функциональной связи. Так, на структурном уровне моделируются ранние этапы проектирования объекта, когда топологической моделью объекта служит ориентированный граф (орграф)(приложение 1) G(V, E), составление которого базируется на содержательном описании состава (множество вершин V) и способа действия объекта (множество ребер Е). Вершинами орграфа vi(элементами объекта) являются, как правило, функционально законченные блоки (части) объекта, а ребрами ej – информационные связи между ними. Структурные отношения между элементами множества V описываются матрицей смежности, строки и столбцы которой соответствуют вершинам орграфа структурной модели, а её aij-й элемент равен числу рёбер, направленных от вершины vi к вершине vi. Отношения между элементами множества V и Е, т.е. между вершинами и ребрами орграфа, описываются в виде булевой матрицы инцидентности, строки которой соответствуют вершинам, а столбцы – рёбрам орграфа; при этом её aij элемент равен +1, если vi – начальная вершина ребра ej, и –1, если vi – конечная вершина ребра ej. На логическом уровне моделирования каждому множеству, булевой матрице бинарных отношений или структурному графу соответствуют наборы логических отношений между входящими в них элементами, представленными в виде логических переменных. Множествам V и E(V) также соответствуют определённые логические отношения, отражающие причинно-следственные связи. Последние описывают последовательности изменения состояний объекта с учётом состояния других, необязательно смежных с ним, объектов. При количественном моделировании каждому элементу множества булевой матрицы или логической переменной ставится в соответствие алгебраическая и другая количественная переменная, а логические отношения переходят в количественные отношения, например, уравнения, неравенства. На каждом из основных уровней моделирования возможны описания объекта с различной степенью полноты и обобщения, так как существуют разные степени детализации структурных, логических и количественных свойств и отношений. Однако задача построения требуемой приближённой модели, которая бы достаточно точно отражала характерные свойства объекта или его элемента на данном уровне проектирования и в то же время являлась доступной для исследования, представляет значительные трудности. Заключение Для каждого этапа выбираются методы и модели системного анализа с учетом конкретных условий и предпочтений лица, принимающего решение (ЛПР). Например, на этапе анализа проблемы возможно использование методов «сценариев», диагностических, «дерева целей», экономического анализа; на этапе анализа структуры системы – диагностических методы, матричные, сетевые, морфологические, кибернетические модели. Таким образом, методика системного анализа разрабатывается для того, чтобы организовать процесс принятия решений в сложных проблемных ситуациях. Она должна ориентировать ЛПР на необходимость обоснования полноты формирования и исследования модели принятия решения, адекватно отображающей рассматриваемый объект или процесс. В методике следует предусмотреть возможность выбора методов моделирования, охарактеризовав их возможности. Приложения 1. 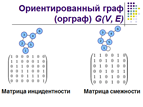 Список литературы 1. [Электронный ресурс]: https://monographies.ru/ru/book/section?id=15759 2.[Электронный ресурс]: https://studopedia.ru/3_61959_metodi-i-modeli-teorii-sistem.html 3. [Электронный ресурс]: https://it.rfei.ru/course/ |

