bestreferat-195274 несколько видов испытаний. Методы и средства измерения температуры
 Скачать 212.02 Kb. Скачать 212.02 Kb.
|
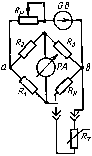 Рис. 1.4. Схема измерения термосопротивления с помощью неуравновешенного моста Зависимость силы тока от изменения сопротивления для неуравновешенного моста определяется по формуле 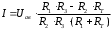 , (1.10) , (1.10)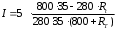 после преобразований получим:  Для удобства перейдем в миллиамперы: 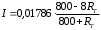 (1.11) (1.11)На основании зависимости (1.11) можно построить таблицу и график изменения силы тока в диагонали измерительного моста в зависимости от изменения сопротивления термопреобразователя и температуры в пределах заданного диапазона измерений. Таблица 1.5 Зависимость силы тока от величины термосопротивления и температуры
 1.4.4 Определяем погрешность измерения, связанную с нелинейностью функции преобразования Наибольшая величина погрешности от нелинейности функции преобразования в пределах диапазона измерений составит л = I – Iл = -2,245- (- 2,337) = - 0,092мА. В относительном виде л = л/Imax 100 % = - 0,092/ 2,430*100= - 3,79 %. 1.4.5 Определяем погрешность измерений при наличии допуска на номинальное сопротивление терморезистора 0,1 Ом Подставим в формулу (1.11) значения 10 0,1 Ом, получим: Погрешность измерений при наличии допуска на номинальное сопротивление терморезистора 0,1 Ом составит R = 0,085 мА. В приведенном виде = R/(Imax – Imin)100 % = 0,085/ (2,430 – ( - 2,245)) 100 % = 1,81 %. 1.4.6 Определить погрешность измерений при падении напряжения Подставим в формулу (1.11) значение напряжения Uав = 5 – 0,2 = 4,8 В. Наибольшая величина погрешности от падения напряжения питания составит u = Imax – Imax = – 2,1 – (–2,245) = 0,145 мА. В относительном виде u = u/Imax 100 % = 0,145/(– 2,245) 100 % = - 6,45 %. Выводы: 1. Шкала измерительного прибора, отградуированная в градусах Цельсия, будет иметь погрешность нелинейности, увеличивающуюся к концу диапазона измерений и равную л = – 3,79 %, это связано с тем, что величина R4 = RT входит в числитель и знаменатель выражения (1.10), являющимся теоретическим выражением функции преобразования для неуравновешенного моста. 2. Погрешность измерений при наличии допуска на номинальное сопротивление терморезистора 0,1 Ом в приведенном виде равна = 1,81 %, она будет оказывать незначительное влияние на погрешность измерений. 3. Погрешность измерений из-за падения напряжения питания на 0,2 В в относительном виде равна u = – 6,45 %, поэтому падение напряжения при применении неуравновешенного моста будет оказывать существенное влияние на результат измерений. ЗАДАНИЕ 2. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЙ ДАВЛЕНИЯ 2.1 Пружинная мембрана манометра диаметром D, толщиной h и модулем упругости ЕG деформируется под действием давления от 0 до δmах. Требуется: 1. Изобразить схему мембраны деформационного манометра. 2. Определить диапазон измеряемых давлений. 3. Определить погрешность измерений, если толщина пружины h выполнена с допуском ±0,01 мм. Сделать заключение о соответствии манометра заданному классу точности. Решение Исходные данные сводим в табл. 2.1. Таблица 2.1 Исходные данные
2.1.1 Схема мембраны деформационного манометра Схема мембраны деформационного манометра приведена на рис. 2.1. 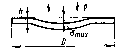 Рис. 2.1. Схема мембраны деформационного манометра 2.1.2 Определяем диапазон измеряемых давлений Механическое напряжение на мембране определяется по формуле 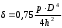 , (2.1) , (2.1)где p – давление, Па; D – диаметр мембраны, мм; h – толщина мембраны, мм. Из формулы (2.1) определяем диапазон измерения давлений при заданных значениях напряжения мембраны: 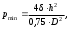 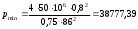 Па ПаВерхний предел измерения 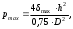 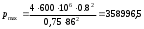 Па Па2.1.3 Определение результата измерения давления при перемещении центра мембраны δ1 Деформация мембраны связана с давлением следующим соотношением 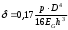 , (2.2) , (2.2)выразим отсюда давление 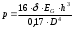 , (2.3) , (2.3)Таким образом, при перемещении мембраны δ1=0,35 мм давление составит 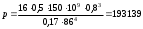 Па Па2.1.4 Определение погрешности результата измерения по классу точности манометра При заданном классе точности 1,0 нормируемое значение абсолютной погрешности измерений будет равно 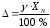 , ,Где γ – приведенная погрешность манометра, % ; 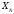 - нормирующее значение, Па: в нашем случае, т.к. рmax = 358996.5 Па принимаем, что верхний предел измерения манометра 350 кПа,т.е. - нормирующее значение, Па: в нашем случае, т.к. рmax = 358996.5 Па принимаем, что верхний предел измерения манометра 350 кПа,т.е. 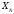 = 350000 Па. = 350000 Па. Па ПаЗапишем результат измерений Р=(193139±5250) Па 2.1.5 Определяем погрешность измерений, если толщина пружины h выполнена с допуском ±0,01 мм Подставим в зависимость (2.1) значения наибольшего давления и величину h с наибольшим и наименьшим размерам 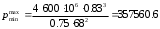 Па Па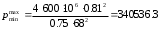 Па ПаНаибольшую абсолютную погрешность определяем по выражению  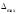 = 357560.6-340536.3=17024,3 Па = 357560.6-340536.3=17024,3 ПаПодставим в зависимость (2,1) значения минимального давления и величину h с набольшими и наименьшими размерами 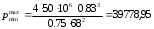 Па Па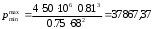 Па ПаМинимальную абсолютную погрешность определяем по выражению 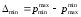 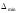 =39778,95-37837,37=1941,58 Па =39778,95-37837,37=1941,58 ПаТаким образом, видно, что погрешность от допуска на изготовления толщины мембраны зависит от измеряемого давления, т.е. является мультипликативной 2.2 Измерение давления трубчато – пружинным деформационным манометром В трубчато-пружинном манометре однотрубная пружина радиусом R0 с первоначальным углом закручивания α = 270° и параметрами поперечного сечения а и b, выполнена из материала с модулем упругости ЕG. Требуется: 1. Изобразить схему пружинно-трубчатого манометра 2. Определить изменения угла закручивания и угла перемещения конца пружины при заданном наибольшем давлении рmах. 3. Определить погрешность измерений, если диаметр трубки D0 выполнен с допуском ±1,0 мм. 4. Назначить класс точности манометра, с учетом запаса точности 2,5. Решение Исходные данные сводим в табл. 2.2. Таблица 2.2 Исходные данные
2.2.1 Схема пружинно-трубчатого манометра Схема пружинно-трубчатого манометра приведена на рис. 2.2.  Рис. 2.2. Схема пружинно-трубчатого манометра 2.2.2 Выбор класса точности трубчато-пружинного манометра для контроля параметра p Определяем допуск контролируемого параметра T=pmax - pmin (2.1) где pmax – наибольшее значение контролируемого параметра, Па; pmin - минимальное значение контролируемого параметра, МПа. Для контролируемого параметра 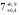 МПа; МПа;наибольшее давление pmax=7,9 МПа; минимальное давление pmin=7,4 МПа T=7,9-7,4=0,5 МПа Допускаемая погрешность измерения контролируемого параметра определяем по формуле: δизм=0,33 T (2.2) δизм=0,33·0,5=0,165 МПа Пределы измерения манометра определяем по формулам: Нижний предел измерения HДИ ≤ pmin - δизм; (2.3) HДИ ≤ 7,4 – 0,165 =7,235 МПа; верхний предел измерения ВДИ ≤ pmax +δизм; (2.4) ВДИ ≤7,9+0,165=8,065 МПа В соответствии с определенными значениями HДИ и ВДИ выбираем манометр с верхним пределом измерений 10 МПа. Приведенную погрешность манометра определяем по формуле 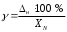 (2.5) (2.5)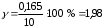 Па ПаПо найденному значению основной приведенной погрешности выбираем манометр класса точности 1,6. 2.2.3 Определяем изменение угла закручивания и угла перемещения конца пружины при заданном наибольшем давлении Угла закручивания связано с давлением соотношением 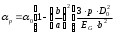 , (2.6) , (2.6)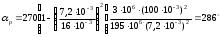 Изменение угла закручивания определяем по формуле Δα=αр – α0 (2.7) Δα=286° - 270=16°. 2.2.3 Определяем погрешность измерения, если диаметр трубки D0 выполнен с допуском ±1,0 мм. Из формулы (2.6) выразим давление 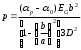 (2.8) (2.8)Подставим в зависимость (2.6) величину D0 с наибольшим и наименьшим размерами   Максимальную абсолютную погрешность определим по выражению 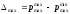 =1,99-1,91=0,08 МПа =1,99-1,91=0,08 МПаПогрешность является мультипликативной, т.к. зависит от измеряемого параметра. 2.3 Измерение давления с помощью пьезоэлектрического преобразователя Напряжение на пьезокристалле кварца преобразователя давления меняется от Umin до Umах, причем используется n пластин толщиной h и размером a b. Емкость измерительной цепи Свх = 10 пФ. Пьезоэлектрическая постоянная для кварца k0 = 2,210-12 Кл/Н и относительная диэлектрическая проницаемость = 4,5. Требуется: 1. Изобразить схему пьезокристалла с заданным количеством пластин. 2. Определить диапазон измерения давления для заданных напряжений 3. Определить систематическую погрешность от влияния внешних физичских величин, в результате чего емкость измерительной цепи Свх увеличится на 5 %. Решение Исходные данные сводим в табл. 2.3. Таблица 2.3 Исходные данные
2.3.1 Схема пьезокристалла Схема пьезокристалла приведена на рис. 2.3. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
