Методы практики. Методы и средства контроля механических свойств микро и нанометровых покрытий и модифицированных приповерхностных слоев

• Название: Методы и средства контроля механических свойств микро и нанометровых покрытий и модифицированных приповерхностных слоев
• Анкор: Методы практики
• Дата: 19.04.2022
• Размер: 0.52 Mb.
• Имя файла: metody-pokrytij.docx
• Тип: Документы; #484422
• страница: 3 из 5

Метод измерительного индентирования

Основы метода измерительного индентирования были разработаны в 1960–70 гг. в СССР, где он был более известен как метод «кинетической твердости» [8]. Широкое распространение в мире метод получил после

íàãðóçêà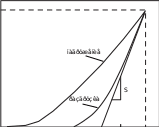
^Pmax

а

ñìåùåíèå

^hf ^hi ^hs ^hmax

A

б
Рис. 4. Алгоритм измерения твердости методом наноиндентирования: а— кривая P(h) зави- симости нагружение–внедрение; б — схематическая иллюстрация измерения параметров кривой P(h), где h_max — максимальная глубина внедрения индентора, h_c — глубина внедре- ния с учетом прогиба поверхности, h_f — глубина восстановленного отпечатка, А_с — проек- ция площади контакта
публикации работы [9], в которой была предложена наиболее согласо- ванная модель анализа экспериментальных зависимостей.

Метод измерительного индентирования заключается в следующем: индентор известной формы под действием нагрузки Рвдавливается

в поверхность образца с постоянной скоростью. При достижении задан- ной нагрузки Р_max или глубины вдавливания h_max движение останавлива- ется на определенное время для выдержки материала под нагрузкой. После этого индентор отводится в обратном направлении. В процессе нагружения и отвода индентора (разгрузки) производится фиксация зна- чений нагрузки и соответствующих смещений. Результирующая зависи- мость представляет собой кривую нагружение-внедрение (рис. 4a).

Используя выбранную теоретическую модель, по данной экспери- ментальной кривой автоматически рассчитывается твердость. Cтандарт ISO 14-577 регламентирует две шкалы твердости:

1. 
   Твердость по Мартенсу HM, равная отношению максимальной на- грузки Р_max к площади A_s поверхности части индентора, внедренной в материал:
   

HM=Ð_max /A_s. (1)


c
При этом A_s рассчитывается, исходя из геометрии индентора. Для иде- ального индентора Берковича A_s= 26,97h².

2. 
   Твердость индентирования H_IT, равная отношению максимальной нагрузки Р_max к площади A_c проекции контакта индентора с поверхно- стью:
   

H_IT = Ð_max/ A_c. (2)


c
Для идеального индентора Берковича A_c= 24,5h².

Определение твердости H_IT авторы считают более предпочтительным с методической точки зрения, т. к. определить площади проекции отпе- чатка значительно проще, чем измерить площадь поверхности части индентора, внедренной в материал. Также определение твердости H_IT имеет очевидный физический смысл среднего контактного давления под индентором и измеряется в паскалях (Н/ м²). Это позволяет перейти при определении значений твердости от безразмерных шкал к физиче- ски осмысленной универсальной шкале твердости.

Для анализа кривых нагружения — внедрения используется метод, предложенный Оливером и Фарром [1]. Как было указано, в рамках данного метода твердость H образца определяется уравнением (2). Наибольшая глубина внедрения h_c индентора в образец вычисляется по формуле:

h_c = h_max – ε P_max / S= h_max – ε (h_max – h_i). (3) Константа ε зависит от геометрии индентора (ε  0,75 для индентора Берковича), h_i — расстояние, соответствующее пересечению касатель-

ной к кривой разгружения в начальной части с осью смещения (рис. 1а). Жесткость контакта Sопределяется по наклону начальной части кривой разгружения P_max:

P= P
S= (dP/ dh) |

max

_. (4)

Площадь проекции А_с определяется из заранее заданной функции формы индентора A(h) при подстановке рассчитанного значения кон- тактной глубины h_c: А_с = A(h_c). Функция формы индентора представля-

ет собой зависимость площади сечения наконечника A от расстояния вдоль оси индентора h. Функция A(h) в рамках данного метода предпо- лагается известной заранее.

Кроме измерения твердости описываемым методом, представляет интерес вычисление эффективного модуля упругости E_r, который по фи- зическому смыслу наиболее близок к модулю Юнга:

E_r = (S/ 2β) (π/ À_с) ^{1 / 2}. (5)

Константа β зависит от формы индентора. Для индентора Берковича с углом при вершине 142° β = 1,034.

Благодаря своей простоте и оперативности получения конечного численного результата описанный метод наноиндентирования на се- годняшний день является единственным теоретически обоснованным, экспериментально подтвержденным и наиболее распространенным способом численного измерения твердости и модуля упругости на суб- микронных и нанометровых масштабах.

Контроль механических свойств методом наноиндентирования ре- гламентируется международными стандартами ISO 14577 [10] и ASTM E 2546–07 [11]. Недавно введен в действие аналогичный ГОСТ Р 8.748–2011.