реферат. Методы коррозионных испытаний
 Скачать 175.51 Kb. Скачать 175.51 Kb.
|
|
Введение Современное развитие химической промышленности, разработка новых технологических процессов, протекающих в агрессивных средах, предъявляют к конструкционным материалам высокие требования. Наиболее важными конструкционными материалами являются металлы и их сплавы. В процессе эксплуатации изделий, вследствие химического или электрохимического взаимодействия их с окружающей средой происходит коррозия. Процессы коррозии необратимы и часто приводят к отказам различных машин и аппаратов, металлоконструкций, поэтому их необходимо обнаруживать на ранних стадиях, давать количественную оценку коррозионного повреждения, прогнозировать опасность развития в случае непринятия мер по усилению коррозионной защиты. Установление причин коррозионного разрушения позволяет правильно выбрать метод защиты. Целью коррозионных исследований является не только определение долговечности данного металла в определенных условиях, но и раскрытие механизма коррозионного процесса, который может быть электрохимическим. химическим или смешанным. Определяется контроль коррозионного процесса: кинетический, диффузионный или смешанный в случае химической коррозии, или виды контроля электрохимических коррозионных процессов. например катодный при основной роли перенапряжения ионизации кислорода. Также устанавливаются агрессивные компоненты внешней среды. например О2, СО2. пары воды, вызывающие химическое коррозионное разрушение металла, или деполяризаторы (О2, Н+, Н2О, HSO3- и др.), способствующие электрохимической коррозии металлов. Изучается влияние внутренних (структура, состав сплава, состояние поверхности, наличие внутренних напряжений и др.) и внешних (состав коррозионной среды, скорость ее движения, температура, давление и др.) факторов на коррозионную стойкость металлов или сплавов. Методы коррозионных испытаний Оценка глубины коррозионного разрушения производится качественными и количественными методами. Качественные методы исследования коррозии Визуальный осмотр. Определение коррозии по именению внешнего вида образца (или какого-либо другого объекта исследования) является самым простым, и вместе с тем самым грубым методом. Однако при правильно поставленных наблюдениях и этот метод может дать ценные качественные и грубо количественные данные. При любых испытаниях необходимо тщательно зарегистрировать состояние образца до опыта. Всевозможные изъяны поверхности, например царапины, рванины, плены, включения и т. п., тоже должны быть отмечены в протоколе опыта. Наблюдения производятся через промежутки времени, продолжительность которых зависит от скорости процесса коррозии. Они должны быть выбраны с таким расчетом, чтобы: а) зарегистрировать начало появления видимых продуктов коррозии, б) изменения между двумя наблюдениями были достаточно резкими. Если образец для наблюдения приходится извлекать из жидкости (испытания в естественных условиях, например, в море), то промежутки необходимо выбирать длиннее, так как каждое такое наблюдение будет сопряжено с нарушением естественного хода процесса коррозии. Лучше сначала производить более частые наблюдения, а затем удлинять промежутки между ними. Результатом наблюдения должны явиться: 1. Регистрация изменений внешнего зида поверхности металла, например: потемнение, покрытие пятнами (такого-то цвета, оттенка), остался блестящим, стал матовым и т. д. 2. Регистрация появления продуктов коррозии, их характер и распределение. Прежде всего отмечается цвет продуктов коррозии, например: белый, коричневый, затем характер, например: хлопья, налет, пленка и т. д.; кроме того, если возможно, отмечают плотность и прочность приставания продуктов к поверхности металла: легко отделяется, не отделяется от металла при легком нажиме и т. н. Визуальное наблюдение внешнего вида образцов применимо во всех случаях коррозионных испытаний и исследований и является ценным вспомогательным средством оценки и выражения коррозии. Визуальное наблюдение за изменениями в растворе. Этот способ качественной оценки применим, естественно, только в лабораторных условиях, т. е. при ограниченном количестве электролита. Если металл переходит в раствор целиком или частью в виде цветного иона, то изменение окраски раствора может служить грубой качественной мерой коррозии. Так, например, в случае коррозии меди в различных электролитах посинение раствора указывает на переход меди в раствор в виде Са+-иона. Если в результате коррозии образуются нерастворимые продукты коррозии, которые плохо удерживаются на поверхности образца и в большей своей части оседают на дно сосуда в виде хлопьевидного осадка, тогда количество осадка служит грубой мерой коррозионного процесса. При испытании железа, меди, алюминиевых сплавов в спокойном нейтральной электролите (например, в морской воде) «горка» осевших продуктов коррозии грубо характеризует степень коррозии. Микроскопическое исследования Дальнейшим развитием визуального метода исследования коррозии металлов является микроскопическое исследование. Так же как и в предыдущих случаях, микроскопическое исследование можно проводить после и во время проведения коррозионных испытаний. Микроскопическое исследование позволяет прежде всего подробно изучать избирательный и локальный характер коррозии; межкристаллигную коррозию, межкристаллитное и внутрикристаллитное коррозионное растрескивание и коррозионную усталость, структурную и экстрагивную коррозию. Микроскопическое наблюдение коррозионных процессов во времени позволяет получить ценные данные о начале и характере развития коррозионных разрушений. Для наблюдения коррозионного процесса под микроскопом поверхность образца — в виде шлифа или подготовленную другим способом — помещают в ванночку так, чтобы рабочая поверхность была повернута к объективу микроскопа. После чего ее наводят на фокус, наливают заранее отмеренное количество коррозионной среды и начинают наблюдение. Индикаторный метод Метод основан на том, что с помощью определ1нных реактивов можно выяснить расположение анодных и катодных участков на поверхности коррозирующего металла по образованию окрашенных соединений при взаимодействии этих реактивов с продуктами коррозии. Этот метод может быть использован при явно гетерогенной коррозии, т.е. при четком разграничении анодных и катодных участков, что может иметь место, например, при грубой неоднородности металла, при наличии неравномерной деформации, при контакте металла с другими металлами и неметаллами. Коррозию железных сплавов в нейтральных водных растворах можнонаблюдать при введении в электролит красной кровяной соли K3Fe(CN)6и фенолфталеина. Если на железном изделии или образце в силу каких-топричин протекает неравномерная коррозия, то катодные и анодныеучастки будут разделены, и в этих местах появится различноеокрашивание. Так, например, если согнуть железную или стальнуюпластинку н опустить ее в воду, то анодный процесс сосредоточится поместу изгиба, вокруг которого вода начнет обогащаться ионамидвухвалентного железа. После добавления в воду красной кровяной солираствор вблизи места изгиба и металл окрашиваются в синий цвет, что иуказывает на присутствие ионов двухвалентного железа: 3Fe + 2Fe(CN)6→ Fe3[Fe(CN)6]2 . При неравномерной концентрации кислорода в водном растворе такжесоздаются анодные или катодные участки, что приводит кнеравномерному разрушению металла и может быть обнаружено также спомощью цветных индикаторов. В качестве примера можно привестикоррозию стальной пластинки под каплей, где вследствие неодинаковойтолщины по сечению капли создается неравномерная растворимость исоответственно неравномерная концентрация кислорода на различныхучастках. На краях капли, где наблюдается повышенная концентрациякислорода, развивается преимущественно катодная реакция: 1/2O2 + H2O+ 2e →2ОH- В середине капли развивается анодная реакция: Fe-2е → Fe2 Это наглядно проявляется, если в каплю (через 20—30 мин. после еенанесения на пластинку) осторожно ввести пипеткой маленькую капелькуфенолфталеина. При этом ободок капли воды сразу же окрасится вмалиновый цвет, что указывает на повышенную концентрацию ионовОН-. Если добавить еще красной кровяной соли. то середина каплиокрасится в синий цвет, что указывает на присутствие ионов Fe2.Описанный метод применяется также при проверке сплошностиискусственных покрытий пассивирующих пленок, полученных тем илииным способом. Для этого поверхность изделия смачивают раствором,содержащим цветной индикатор или покрывают смоченной в этом растворефильтровальной бумагой и наблюдают за появлением окрашенных точек.Для железных сплавов в состав раствора всегда вводят красную кровянуюсоль с небольшими добавками соляной кислоты или хлористого натрия(С1-). Если покрытие имеет поры, то через 3-5 минут появляются синиеточки.Для проверки сплошностипассивирующей пленки на алюминии всостав раствора вводят бихромат калия (K2Cr2O7) с соляной кислотой. Если пленка пористая, то через 2-4 минуты цвет раствора меняется от желтого до зеленого. Это указывает на протекание реакции окисления алюминия и восстановления хрома до трехвалентного иона: 2А1 + Сr2O72- + 14Н → 2А13+ + 2Сr3++ 7Н2O Сплошность толстой оксидной пленки на таких металлах, как магний и алюминий, можно проверить с помощью солей ртути или самой ртути. В тех местах, где пленка повреждена или пориста, начинаетсябурное окисление металла в воздухе с образованием поросли окислов.Окисление металла сосредоточивается в тех местах, где ртутьконтактирует с металлом, и на поверхности образуется амальгама.Атомы металла.растворяясь в амальгамеоказываютсянезащищенными от внешней среды и легко вступают во взаимодействиес ней. На место ушедших из раствора поступают новые атомы изкристаллической решетки металла. Таким образом, окислениепродолжается до тех пор, пока ртуть не исчезает в результатерастворения в металле или испарения. Схема окисления металла подамальгамой показана на рис. 2. Коррозия металлов под амальгамой носит неравномерный точечныйхарактер.При испытании металлов на интеркристаллитную коррозию наиболеепростым методом является определение звука при ударе; металл,подверженный интеркристаллитной коррозии, теряет при этомхарактерный для него металлический звук. Это можно наблюдать налатуни при действия на нее растворов ртутных солей. Латунная пластинка,выдержанная в таком растворе в течение 20-30 минут при ударе теряетметаллический звук, становится хрупкой, при изгибе ломается или даеттрещины.Чувствительность к интеркристаллитной коррозии нержавеющих сталейопределяется кипячением в стандартном растворе следующего состава: 111гCuSO4 • 5Н2О + 55мл H2SO4 (удельный вес - 1,84) на 1л воды. Количественные методы исследования коррозии Весовой метод Данный метод основан на определении измерения массы образцов после воздействия агрессивной среды. При этом определяют прибыль или убыль массы образца. В первом случае после действия агрессивной среды взвешивают образцы, собрав все продукты коррозии, во втором необходимо все продукты коррозии удалить. 3.2.2. Объемный метод Объемный метод изучения скорости коррозии основан на определении количества выделившегося при реакции водорода ( при коррозии в кислой среде с водной деполяризацией) или поглощенного кислорода (при коррозии в нейтральных средах с кислородной деполяризацией). Объемный метод в 10 - 100 раз более точен, чем весовой, и позволяет определить зависимость скорости коррозии от времени, не удаляя продукты коррозии и не прерывая испытания. Сущность объемного метода заключается в определении количества газа,выделяющегося или поглощающегося в процессе электрохимической коррозии. Лабораторные методы исследования коррозии Общие методы исследования коррозии металлов в электролитах Среди лабораторных.коррозиoнных испытаний наиболее важными являются так называемые ускоренные коррозиoнные испытания, в которых создаются условия, вызывающие быстрое коррозионное разрушение вследствие увеличения агрессивности среды. Основные среды для лабораторных коррозиoнных испытаний – электролиты, влажная атмосфера, содержащая или не содержащая коррозионноактивные вещества (NaCl, SO2, CO2 и т.п.), без конденсации или с периодической конденсацией влаги; газовые среды с повышенной температурой; почвы, нефтепродукты, расплавленные соли, жидкие металлы. Наиболее простым и доступным методом определения коррозионной стойкости металлов в электролитах является испытание в открытом сосуде, которое позволяет исследовать большинство показателей коррозии. Образцы (обычно три в каждом опыте) подвешивают на стеклянном крючке или капроновой нити и испытывают при полном, частичном или переменном погружении в неподвижный раствор, через который можно пропускать воздух, кислород, азот или другой газ. Более совершенно проведение испытания в оборудованном термостате. Если испытания проводятся при повышенных температурах, вместо открытых стаканов применяют колбы, снабженные обратными холодильниками. Образцы при этом подвешивают на стеклянных или фторопластовых подвесках, крепят в стеклянных подставках, помещают на дно колбы, переложив их стеклянной ватой. Простой метод коррозионных испытаний металлов в электролитах, например, в кислотах, при высоких температурах и давлениях состоит в выдержке исследуемого образца металла, помещенного в запаянную ампулу из термостойкого стекла с налитым в нее электролитом, при заданной температуре в термостатированном шкафу. Для предупреждения разрыва запаянных ампул вследствие образования в них паров электролиза и накопления газообразных продуктов коррозии ампулы помещают в контейнеры, изготовленные из нержавеющей стали, у которых для создания противодавления пространство между стенкой и ампулой заполняют водой. Более совершенным методом коррозионных испытаний в электролитах при высоких температурах и давлениях является проведение их в специальных автоклавах. Прибор для массовых сравнительных коррозионных испытаний металлов при полном погружении в электролит, в которомпредусмотрены постоянное перемешивание раствора и термоконтроль, носит название шпиндельного аппарата. Для подобного рода коррозионных испытаний металлов при переменном погружении в электролит применяют различные аппараты, которые представляютсобой застекленные термостатированные камеры с автоматическиподнимающейся и опускающейся штангой с подвешенными к нейиспытуемыми образцами. Для простейших лабораторных испытаний металлов на атмосферную коррозию исследуемые образцы одного или нескольких металлов помещают в закрытый эксикатор, на дно которого налита вода. Для более интенсивного осаживания влаги образцы одни или два раза в сутки охлаждают в термосе, после чего их переносят в эксикатор для коррозионных испытаний, имеющий комнатную температуру. Массовые сравнительные коррозионные испытания металлов во влажной атмосфере проводят во влажной камере — термостатированном застекленном обычным или органическим стеклом шкафу, в котором периодически распыляется по заданному режиму коррозионный раствор (водопроводная, морская, рудничная вода, раствор, имитирующий промышленную атмосферу). Камеры бывают с неподвижно расположенными и передвигающимися испытуемыми образцами. Недостаток камеры с неподвижными образцами — зависимость скорости коррозии от места расположения образцов в камере. В камерах с передвигающимися образцами этот недостаток устранен, так как все образцы проходят одни и те же участки камеры. В камере этого типа рекомендуется помещать образцы на вращающееся вертикально колесо, к прорезям текстолитовых кругов которого образцы привязывают капроновыми нитями. Модели поверхностного коррозионного разрушения При построении моделей поверхностного коррозионного разрушения нужно иметь виду, что может быть несколько причин, приводящих к изменению расчетных схем, и несколько параметров, характеризующих эти изменения. Поэтому математические модели, учитывающие влияние агрессивной среды на состояние поверхности конструкций, можно разделить на три группы: • изменение глубины коррозионного разрушения д зависит только от времени взаимодействия материала со средой; • изменение глубины коррозионного разрушения д функционально зависит от нескольких характеристик агрессивной среды, например; где t - время взаимодействия элемента конструкции с агрессивной средой; Т - температура, В - концентрация агрессивной среды; • несколько различных параметров поврежденности, характеризующих степень коррозионного разрушения элемента, зависят от одного фактора, например, от времени контакта элемента конструкции с агрессивной средой. В каждой из указанных групп моделей встречаются модели с обратными связями, более точно отражающие реально проходящие процессы коррозионного разрушения. Примером модели с обратной связью может служить зависимость вида где S - глубина разрушенного коррозией слоя в элементе конструкции, су - напряжение в этом слое. Ясно, что если глубина коррозии с течением времени увеличится, то это приведет к уменьшению сечения элемента, а, следовательно, к увеличению напряжения, что в свою очередь увеличит глубину разрушенного коррозией слоя. Это - математическая модель процесса коррозионного разрушения с положительной обратной связью. Далее рассмотрим некоторые известные из литературных источников модели коррозионного повреждения материала конструкций, которые относятся к группе моделей с внешним параметром поврежденности. Одной из первых моделей, описывающих разрушение металла под влиянием агрессивной среды, является закон Фарадея, связывающий потерю веса G (параметр поврежденности) металла, подвергающегося электрохимическому растворению, с величиной тока i и временем протекания процесса t. здесь а - постоянная величина, учитывающая свойства материала и характер агрессивной среды. Детальные исследования процесса электрохимического растворения металлов под действием блуждающих токов в атмосфере, воде, грунте и других средах позволили установить, что постоянная а в законе Фарадея не постоянна, а изменяется. П.Азизом [87], Г.Чампионом [88], Ж.Меткалфом [89] предложена нелинейная модель коррозионного процесса, связывающая глубину коррозионного повреждения Sk (параметр поврежденности) с характеристиками агрессивной среды и временем: где к и а - постоянные величины, характеризующие процесс коррозионного разрушения. Эта зависимость не отражает того известного факта, что скорость коррозии в начальный период возрастает, затем становится постоянной и, наконец, уменьшается. А. Лиддард и Б. Виттакер [90] предложили модель коррозионного разрушения в следующем виде где к и а - постоянные, отражающие влияние среды на процесс коррозионного разрушения. Эта зависимость обладает тем же недостатком, что и предыдущая. В работах Н. Годарта [91] и Ж. Ф. Друмма [92] предложены однопараметрические модели коррозионного разрушения, родственные друг другу и имеющие вид: Эта модель была обобщена Н. Денисоном в следующем двухпараметрическом виде Как видно, эти модели не что иное, как различные варианты степенной зависимости параметра поврежденности (глубины коррозионной каверны) от времени t. Кривые, соответствующие этим зависимостям, недостаточно точно описывают процесс коррозионного разрушения и потому применяются редко. Н.Д. Томашов [93] для описания коррозионного разрушения металла использовал зависимость, предложенную в 1920 г. Г. Тимманом Здесь 5 - толщина окисленного слоя; к - постоянная, зависящая от коэффициента диффузии и концентрации кислорода. Более сложный закон роста сплошной пленки окислов металлов, приведенный в работе Л.Я. Цикермана [94], имеет вид: где показатель п не всегда равен двум. Для ряда металлов (алюминий, цинк, никель, железо) установлена логарифмическая зависимость Описанные выше зависимости в основном описывают процесс коррозионного повреждения металла в атмосфере. Л.Я. Цикерманом [95] была предложена трехпараметрическая модель коррозионного разрушения металла в грунте здесь а, b, S0 - постоянные, характеризующие влияние среды на процесс коррозионного разрушения. Математическая модель (6.10) описывает в основном электрохимическую коррозию. Л.Я. Цикерманом приведен упрощенный двухпараметрический вариант модели (7.10) который идентичен модели, описывающей атмосферную коррозию. Им же предложена трехпараметрическая модель коррозионного разрушения, в которой в качестве величины, характеризующей коррозию, принята скорость грунтовой коррозии V: 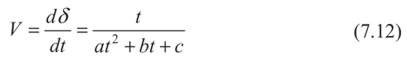 где а, Ь, с - постоянные параметры, характеризующие влияние среды. Я.П. Штурманом [96] предложена модель коррозионного разрушения в виде дробно-линейной функции:  Эта модель, по мысли ее автора, пригодна для описания грунтовой коррозии металла. Я.П. Штурман предложил использовать ее и для описания атмосферной коррозии металла, только брать в качестве параметра поврежденное™ вес металла, разрушаемого в результате коррозии: Здесь G0 и Г - постоянные, характеризующие свойства металла и среды. Зависимость (7.13) изображена на рис. 7.1. 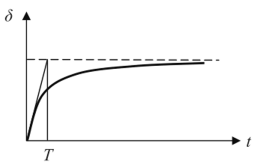 Рис. 7.1 В.А. Притула предложил двухпараметрическую модель грунтовой коррозии металла в виде где а и b - параметры, характеризующие условия протекания коррозионного разрушения. И. Палмер, А. Коупер и И. Горман, исследуя коррозию углеродистой, хлористой и нержавеющей сталей в сероводородных средах, пришли к выводу о том, что скорость коррозии в этом случае можно описать с помощью модифицированного уравнения Аррениуса: где Vk - скорость коррозии; Т- температура по Фаренгейту; Р - общее давление (в фунтах на кв. дюйм); (CW 5) - молярная концентрация H2S в рабочем технологическом процессе; А, В, D, Е— параметры, характеризующие процесс взаимодействия металла со средой. Е. Вальнер [97] экспериментальным путем установил, что скорость коррозии малоуглеродистой или низколегированной бесфосфористой стали, изменяется по закону  где Ann- постоянные, причем показатель степени п зависит от агрессивности среды, а коэффициент А - от состава стали. Заметим, что формально модель (7.17) совпадает с (7.16), однако здесь в качестве определяемого параметра принята скорость коррозии, а не глубина каверны. У. Джонсон [98], исследуя коррозию алюминия в водопроводной воде, установил, что развитие питтинга (точечной коррозии) после инкубационного периода происходит по закону который в точности совпадает с уравнением (7.5). Процесс окисления никельхромовых сплавов протекает по более сложному закону, зависящему от температуры и типа сплава. На первой стадии кинетика окисления подчиняется логарифмическому закону: а затем закону В этих выражениях ^ ,к2 ,к, п - постоянные величины, определяемые на основании опытных данных. Анализируя приведенные выше математические модели коррозионного процесса можно отметить, что при их построении авторы идут двумя путями. Первый состоит в учете многочисленных внешних воздействий, вызывающих коррозию металла, и выявлении степени влияния каждого фактора на процесс коррозии экспериментальным путем. Второй путь заключается в разработке математической модели коррозионного процесса в виде функционального или дифференциального уравнения, по возможности более или менее точно аппроксимирующего реальную кинетику коррозионного разрушения. Координата фронта диффузии продукта метаболизма в композит может быть оценена по формуле где К(<^) - коэффициент, зависящий от изменения концентрации среды по толщине изделия, ? = 1 - c(x,t) С0 Если некоторые компоненты материала являются источниками питания микроорганизмов, то  п - концентрация веществ, усваиваемых микроорганизмами, Кх - константа скорости взаимодействия веществ. Диффузионная модель деградации характерна для полимерных композитов. В экспериментах использованы карбамидные, эпоксидные, полиэфирные композиты. Агрессивная среда - это 10% серная кислота и вода. Выдержка - 90 суток. Изменение модуля упругости может быть описано степенной зависимостью.  при полном разрушении материала на поверхности 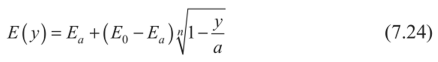 здесь awn — определяются из эксперимента. Таким образом, при математическом моделировании можно использовать модели поверхностного разрушения материала конструкции, причем из-за отсутствия экспериментальных данных, приходится считать, что скорость коррозионного разрушения не зависит от величины и вида напряженного состояния. Сравнивая описанные выше модели коррозии можно заметить, что для описания процессов коррозионного повреждения в различных средах используются нередко похожие или даже совпадающие математические модели. Экспериментальные данные, полученные в натурных и лабораторных условиях, и расчеты, проведенные Л. Я. Цикерманом, подтверждают, что процесс коррозионного разрушения металлов в различных средах (грунте, атмосфере, морской и пресной воде, зонах периодического увлажнения, атмосфере промышленных предприятий), а также разрушение стальной арматуры в бетоне феноменологически сходны. Поэтому он предлагает описывать процесс коррозионного поражения различных металлов в разных агрессивных средах общей математической моделью либо в виде дробно-линейной функции  либо в виде экспоненциальной зависимости Графики этих функций приведены на рис. 7.2 (кривая 2). Экспериментальную кривую 1, полученную Л. Я. Цикерманом, можно разбить на два участка: первый - до точки перегиба и второй - после точки перегиба. На первом участке наблюдается интенсивное увеличение скорости коррозии, сопровождающееся большими потерями металла, на втором коррозия затухает. Это объясняется тем, что продукты коррозии, закрывая поверхность металла, уменьшают контакт его с агрессивной средой и тем самым способствуют замедлению процесса коррозионного разрушения. 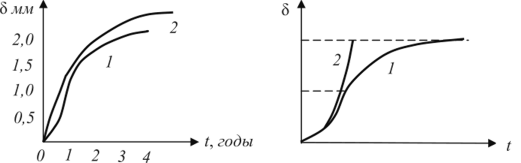 Рис. 7.2 Сопоставление теоретических кривых с экспериментальной кривой позволяет отметить, что функции (7.25) и (7.26) удовлетворительно описывают экспериментальную кривую за точкой перегиба, но качественно неверно описывают коррозионный процесс на первом участке, так как они в состоянии описывать только процесс с уменьшающейся с течением времени скоростью. На правом рисунке (рис. 7.2) показана экспонента I и логистическая кривая 2, которая соответствует экспериментальной кривой. Для преодоления указанных затруднений Л .Я. Цикерман предложил модель коррозионного процесса в виде дифференциального уравнения второго порядка: 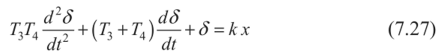 где Г, и Т4 — параметры коррозионного процесса; к - так называемый коэффициент передачи; х - характеристика агрессивных свойств внешней среды, с которой контактирует металл. Решение этого уравнения имеет вид 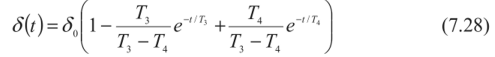 Характер этой кривой соответствует экспериментальной кривой (рис. 7.2), однако пользоваться этой зависимостью трудно ввиду ее сложности. Кроме того, функция (7.28) является решением линейного уравнения (7.27), которое нелинейный процесс коррозионного разрушения описывает приближенно. Для описания процесса коррозионного разрушения во времени построим математическую модель в виде нелинейного дифференциального уравнения. Процесс коррозионного разрушения на начальном его этапе (до точки перегиба, рис. 7.2) опишем дифференциальным уравнением где к - постоянная величина, характеризующая отклик на глубину коррозионного разрушения. Это уравнение показывает, что скорость роста слоя, пораженного коррозией —, пропорциональна достигнутой глубине S, dt 1 dS или относительная скорость коррозии--остается постоянной величи- 5 dt ной. Решая (7.29), получаем уравнение экспоненты соответствующей начальному участку кривой. Механизм коррозионного разрушения, заданный уравнением (7.29), сохраняется до точки перегиба, а затем должны проявить себя сдерживающие факторы из-за уменьшения контакта металла с агрессивной средой вследствие защитного действия продуктов коррозии. В этом случае проким образом, чем больше глубина коррозии, тем меньше скорость ее нарастания. Решение дифференциального уравнения (7.32) имеет вид  цесс коррозионного разрушения можно представить дифференциальным уравнением в котором рост коррозии ограничен; S0 - максимальная глубина коррозии. Относительная скорость коррозии линейно убывает с ростом 8 - глубины коррозии (00,?>0). Таи называется логистической кривой Ферхюльста. Графическое изображение ее приведено на рис. 7.2. В начальные моменты времени, когда 8<8п, логистическая кривая совпадает с экспонентой. Прямые 8 = 80 и 8 = 0 являются асимптотами логистической кривой. При 8 = 80 /2 логистическая кривая имеет точку перегиба, в которой меняется знак ускорения. Логистическая кривая дает хорошие результаты в математической статистике при описании роста какой-либо совокупности - клеток, людей, популяции животных, эпидемий. Можно предполагать, что она позволит достаточно точно описать такой распространенный процесс, как коррозионное разрушение. Таким образом, применение рассмотренных выше моделей поверхностного разрушения материала конструкций приводит к следующему алгоритму. 1. Выполняем расчет конструкции и определяем ее размеры, обеспечивающие заданные критерии прочности и деформативности. 2. В соответствии с применяемым материалом и видом агрессивной среды берем одну из рассмотренных выше моделей или выбираем подходящую модель в справочной литературе и задаем время надежной эксплуатации конструкции (долговечность). 3. По заданной долговечности вычисляем толщину пораженного коррозией слоя и добавляем ее к размерам конструкции, определенным в первом пункте. 4. Для определения запаса прочности конструкции определяем толщину слоя поврежденного коррозией в соответствии с выбранной моделью и известному времени эксплуатации конструкции в агрессивной среде. Определяем текущие размеры конструкции. Далее производится поверочный расчет конструкции с текущими размерами и делается заключение о соответствии его НДС прочностным и деформационным критериям. В описанных выше математических моделях влияние напряженно- деформированного состояния на процесс коррозионного разрушения не учитывалось. Однако это влияние во многих случаях может оказаться столь значительным, что им нельзя пренебрегать. Впервые влияние напряжений на скорость коррозии в расчетах на прочность было учтено В.М. Долинским. Величина скорости коррозии в первых работах В.М. Долинского считалась линейной функцией абсолютной величины напряжений. В последующих его работах скорость коррозии принималась в виде линейной функции интенсивности напряжений <т. где У0 - скорость коррозионного разрушения ненапряженного элемента; m - коэффициент, учитывающий влияние напряженного состояния на скорость коррозии. Глубина разрушаемого слоя элемента конструкции с учетом уравнения (7.34) определится следующим образом: 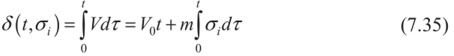 В.Г. Карпунин [99] предложил модель коррозионного разрушения в виде дифференциального уравнения первого порядка с начальным условием J(x,^,0) = 0. Здесь х, у — координаты точек поверхности рассматриваемого элемента конструкции;/- функция, учитывающая влияние времени коррозионного процесса и уровня действующих напряжений; а <7 - некоторая функция, характеризующая напряженное состояние в точке разрушаемой поверхности элемента конструкции. Вид функции f(t,cr) принимается на основе экспериментальных данных. При построении этой функции предлагается представлять ее в виде произведения двух функций, одна из которых зависит только от времени t, а другая является линейной функцией интенсивности напряжений сг, например Вид безразмерной функции (p{t), а также значения коэффициентов a,j3 находятся экспериментальным путем, причем функцию можно приближенно задавать в виде Очевидно, что модель (7.37) допускает обобщение. Например, можно принять: где п - также определяется экспериментальным путем. Используя эту модель, В.Г. Карпунин выполнил исследование прочности и устойчивости пластинок и оболочек с учетом коррозионного износа. Э. М. Гутман предложил уравнение коррозионного разрушения материала, в котором скорость коррозии определяется ускорением анодного растворения в результате действия механических напряжений:  Здесь Vo - скорость коррозии ненапряженного материала; М - мольный объем коррозируемого материала (для железа М = 7 см3, для алюминия М = 10 см3); Т - температура процесса в градусах Кельвина; R - газовая постоянная. Если материал элемента представляет собой сплав, то мольный объем сплава определится так:  где р. - доля каждого компонента в сплаве; М. - мольный объем этого компонента. Величина <7 в уравнении (7.40) представляет собой шаровой тензор напряжений (среднее напряжение). Однако в практических расчетах при использовании этой математической модели рекомендуется вместо среднего напряжения использовать максимальное главное напряжение, которое и будет определять скорость коррозии. При расчете, например, элементов в условиях одноосного напряженного состояния под <7 нужно понимать среднее напряжение. Сравнение теории с экспериментом, проведенное Г.В. Акимовым, подтверждает это. Заметим, что уравнение (7.40) учитывает также влияние на коррозионный процесс температуры. И.В. Овчинников предложил учесть влияние на скорость коррозионного разрушения не только напряженное, но и деформированное состояние элемента конструкции. Разрушение - это необратимый процесс, часть высвобождаемой при разрушении энергии идет на повышение потенциала разрушаемого элемента за счет искажений внутренней структуры материала. Поэтому скорость накопления коррозионных повреждений предполагается пропорциональной удельной энергии деформирования разрушаемого слоя поверхности, то есть  где сг - интенсивность напряжений; - интенсивность деформаций; <т); - пороговый уровень напряжений, начиная с которого, влияние агрессивной внешней среды приводит к ускорению процесса коррозионного разрушения материала (причем, если сг = <7п, то сг - <7п = 0); /3 - скорость коррозии материала, уровень напряжений в котором ниже порогового; а - коэффициент, учитывающий влияние напряженно-деформированного состояния на скорость коррозии в конкретной агрессивной среде. Как видно, в модель коррозионного процесса (7.42) время t явно не входит. Его можно ввести следующим образом Функция (p{t) и коэффициенты а,/3,т определяются по результатам экспериментов. Функцию cp{t) можно принять в виде (7.38). При выборе математической модели нужно учитывать условия протекания рассматриваемого процесса коррозионного разрушения путем выбора подходящей модели, а не путем усложнения, часто неоправданного, какой-либо одной модели. Если в процессе коррозии материала прокорро- дированный слой растворяется или существенно разрыхляется, то его можно исключить из рассмотрения при расчете конструкции. Таким образом, имеем дело с конструкцией, у которой с течением времени изменяются размеры поперечного сечения (балки и стержни), или толщина (пластинки и оболочки). Если прокорродированный слой продолжает сопротивляться внешней нагрузке, и только изменились его прочностные и деформационные характеристики, то мы имеем дело с наведенной неоднородностью свойств. Характер изменения этих свойств определяется экспериментально. Таким образом, применение рассмотренных выше моделей коррозии под напряжением приводит к следующему алгоритму определения долговечности конструкций. 1. Выполняем расчет конструкции и определяем ее размеры, обеспечивающие заданные критерии прочности и деформативности. 2. В соответствии с материалом конструкции и видом агрессивной среды выбираем одну из рассмотренных выше моделей или выбираем подходящую модель в справочной литературе. 3. Время взаимодействия с агрессивной средой представляем в виде суммы малых временных инкрементов (последовательных приращений). Изменение размеров на первом временном инкременте определяем по выбранной модели в соответствии с НДС конструкции, полученным в п.1. 4. Рассчитываем конструкцию с измененными размерами на действие первоначальной нагрузки и определяем параметры НДС необходимые для применения выбранной модели. 5. Определяем изменение размеров конструкции на втором временном инкременте в соответствии с пунктами 2 и 4. Корректируем текущие размеры конструкции. 6. Снова рассчитываем конструкцию с дополнительно измененными размерами на действие первоначальной нагрузки и определяем параметры НДС необходимые для применения выбранной модели. 7. Далее производим аналогичные действия последовательно для всех временных инкрементов до момента достижения конструкцией опасного состояния. Сумма временных инкрементов, по принятому определению, определяет долговечность конструкции. |
