занятие 3. Методы оценки взаимодействия факторов. Метод стандартизации
 Скачать 472.31 Kb. Скачать 472.31 Kb.
|
|
МЕТОДЫ ОЦЕНКИ ВЗАИМОДЕЙСТВИЯ ФАКТОРОВ. МЕТОД СТАНДАРТИЗАЦИИ. Одной из важных задач, решаемых с помощью статистического метода, является определение наличия взаимосвязи между различными признаками и явлениями. Для медицины это имеет огромное значение. Только объективная оценка и целенаправл.влияние на различные факторы может привести к эффективному решению вопросов и задач профилактики, диагностики, лечения, реабилитации, эффективному управлению и использованию ресурсов здравоохранения. Понятие о функциональной и корреляционной зависимости. Различают две формы взаимосвязи между признаками: функциональную и корреляционную. При функциональной связи (зависимости) каждому значению (величине) изучаемого признака соответствует только одно определенное значение другого взаимосвязанного с ним признака. Изменение одной величины обязательно приводит к изменению другой на строго определенную величину. Функциональная связь – связь «низкого уровня», характерная для физико-химических явлений, математики. Например, зависимости скорости, расстояния и времени; радиуса и площади круга и др. Такая форма связи не является предметом рассмотрения медицинской статистики, так как ее наличие очевидно и не требует уточнения, а для выявления новых форм функциональной связи статистические методы не являются определяющими. Под корреляционной связью (зависимостью) понимают такую связь, при которой одной величине изучаемого признака соответствует несколько других величин, взаимосвязанного с ним признака, варьирующих около своей средней. Изменение одной величины может вести к изменению другой на различные значения. Под прямой корреляционной зависимостью понимают такую связь, когда увеличению (сни жению) одной величины соответствует увеличение (снижение) связанной с ней другой. Например, интенсивность курения ведет к увеличению риска развития ишемической болезни сердца, с увеличением возраста ребенка увеличивается его масса тела и др. Под обратной корреляционной зависимостью понимают такую зависимость, когда увеличению (снижению) одной величины соответствует снижение (увеличение) связанной с ней другой. Например, курение снижает среднюю продолжительность жизни; уменьшение времени ожидания приема врача увеличивает удовлетворенность пациентов медиц. помощью; сокращение сроков доставки пациентов с острой хирургической патологией в стационар от момента начала заболев-я снижает послеопер.летальность и др. Корреляционная связь может иметь различную силу, быть слабой, средней, сильной. В зависимости от этого корреляционная связь может быть очевидна: с увеличением роста увеличивается масса тела; с повышением температуры тела увеличивается частота сердечных сокращений и др. Однако большинство сложных явлений общественного здоровья, организации здравоохранения, вопросов рофилактической и клинической медицины имеют завуалированные, зависящие от многих причин взаимосвязи. Именно на выявлении и количественной оценке такой формы связи сосредоточено внимание мед.статистики, которая должна в рамках корреляционного анализа ответить на вопросы: определить наличие или отсутствие связи; определить направление связи; определить силу связи; определить достоверность результатов исследования Параметрические и непараметрические методы расчета коэффициента корреляции. Существует большое количество различных параметрических и непараметрических методик определения корреляционной зависимости. При параметрических методах вычисления проводят с реальными полученными количественными данными, имеющими симметричное распределение в статистической совокупности. При асимметричном распределении или при необходимости провести корреляционный анализ качественных признаков применяют непараметрические методы. Непараметрические методы в отличие от параметрических менее точны, но позволяют проводить корреляцию как между количественными, так и между качественными признаками. Наиболее простыми являются параметрический метод расчета коэффициента корреляции Пирсона (r) и непараметрический метод расчета коэффициента корреляции Спирмена (). Значения коэффициента корреляции интерпретируют следующим образом (таблица):
Ранговый метод определения коэффициента корреляции. КОЭФФИЦИЕНТТ КОРРЕЛЯЦИИ СПИРМЕНА: 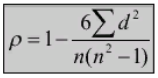 где: - коэффициент ранговой корреляции; d – разность рангов (порядковые номера рядов) n – число коррелируемых пар рядов. Пример вычисления коэффициента ранговой корреляции. Существует мнение, что уровень рождаемости в регионе зависит от доли сельского населения. Необходимо найти наличие, направление и силу связи и сделать вывод. В таблице 14 в первых двух графах располагаются данные о доле сельского населения в различных регионах России и соответствующих уровнях рождаемости. В следующих графах последовательно вычисляется сумма квадратов разности рангов. 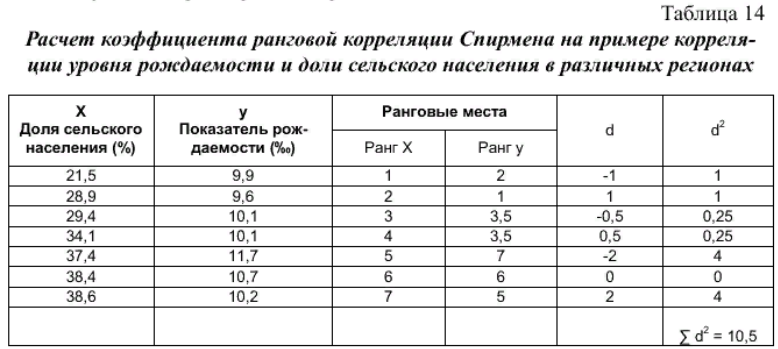 Вначале необходимо расположить данные одного из рядов (x) в порядке возрастания (в таблице они уже расставлены). Так как значения второго ряда (y) связаны со значениями первого ряда, то естественно равномерного их увеличения или снижения может и не быть. Для каждого из рядов определяем ранги, т.е. расставляем порядковые номера значений по возрастанию. Т.к. во втором ряду имеется два одинаковых значения показателя рождаемости, то для каждого из них вписываем значение средней арифметической их порядковых номеров. В следующей графе построчно определяем разность рангов. В последней графе построчно возводим разность рангов в квадрат, и получаем сумму квадратов разности рангов. Полученные данные подставляем в формулу. 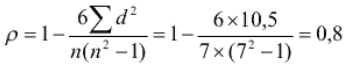 Прежде чем делать вывод необходимо оценить достоверность значения полученного коэффициента, вычислив ср.ошибку коэффициента ранговой корреляции и критерий достоверности: 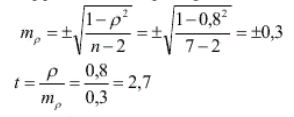 На основании полученных данных можно сделать вывод о сильной прямой корреляционной зависимости уровня рождаемости в различных регионах от доли сельского населения. Т.е. чем выше доля сельского населения в регионе, тем выше уровень рождаемости. Поскольку критерий достоверности более 2, данный вывод можно считать достоверным с вероятностью более 95,5%. Сущность, значение и применение метода стандартизации. При сравнительном анализе показателей общественного здоровья и здравоохранения всегда возникает вопрос: чем обусловлены имеющиеся в них различия. Так, например, при сравнении показателей смертности в РФ и странах Западной Европы в 2004 г. (17‰ и 10 ‰ соответственно) возникает вопрос, почему смертность в России гораздо выше, чем в странах Западной Европы. Различия в этих показателях могут быть обусловлены не только действительными отличиями в размерах смертности, но и разницей в возрастном, половом, социальном составе населения, различиями в уровне, укладе и качестве жизни, санитарно-гигиенических условиях проживания, наличием в составе Российской Федерации регионов с наиболее неблагополучной и нестабильной обстановкой. Выявление истинных причин этого явления сложно, но необходимо для проведения целенаправленной госуд.политики, направленной на снижение смертности. Поэтому при сравнении показателей рождаемости, смертности, заболеваемости, инвалидности и др. обычно применяют метод стандартизации, позволяющий нивелировать различия в структуре изучаемого явления. Метод стандартизации позволяет рассчитать стандартизированные показатели, определяя, какими бы были истинные размеры изучаемых явлений, если бы состав сравниваемых совокупностей был одинаков. Существует три метода расчета стандартизированных коэффициентов: метод прямой стандартизации, метод обратной стандартизации и метод косвенной стандартизации. Метод прямой стандартизации может применяться, когда известен как размер изучаемого явления, так и состав среды (например, известны уровни смертности и возрастной состав населения). Метод обратной стандартизации применяется, когда имеются данные о размерах изучаемого явления, но отсутствуют данные о составе среды. Метод косвенной стандартизации применяется, когда отсутствуют данные о размерах изучаемого явления, но есть данные о составе среды. Методика вычисления и анализ стандартиз.показателей прямым методом стандартизации. Прямой метод стандартизации включает в себя следующие этапы: 1) расчет общего и погрупповых интенсивных показателей; 2) выбор стандарта; 3) расчет ожидаемых величин; 4) расчет стандартизированных показателей; 5) сравнение стандартиз.показателей между собой и истинными интенсивными показателями. Пример расчета стандартизированных показателей. В таблице 15 приведены данные об общей заболеваемости населения ЗНО в районе К. в 1996 и 2006 гг. в различных возрастных группах. Рассчитав стандартизированные показатели мы ответим на вопрос, повлияли ли изменения возрастного состава населения на изменения в показателях заболеваемости ЗНО. 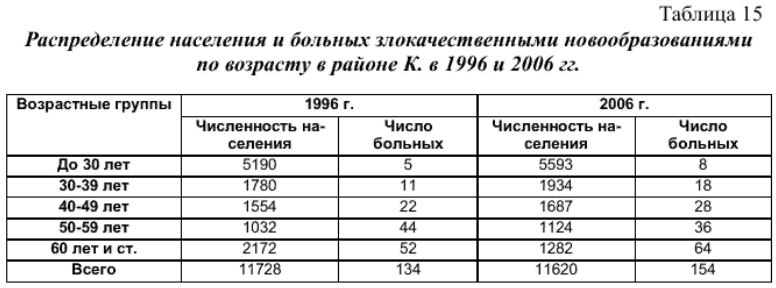 1) Рассчитаем общий и погрупповые интенсивные показатели и занесем их таблицу 16 Так для возрастной группы до 30 лет показатель общей заболеваемости ЗНО в 1996 г. составил:  Из таблицы 16 видно, что за десять лет общая заболеваемость в районе «К» ЗНО выросла с 114,3 до 132,5 случаев на 10000 населения. 2) Выберем стандарт. За стандарт можно взять возрастной состав населения как в 1996 так и в 2006 году, можно взять суммарный возрастной состав за эти годы. Примем за стандарт возрастной состав в населения в 1996 г. (таблица 18). В этом случае стандартизированный показатель необходимо будет рассчитать только для 2006 года, т.к. выбирая такой стандарт, мы задаем вопрос: какими бы были показатели общей заболеваемости населения ЗНО в районе «К» в 2006 г., если бы возрастной состав жителей района был бы такой же, как и в 1996г. 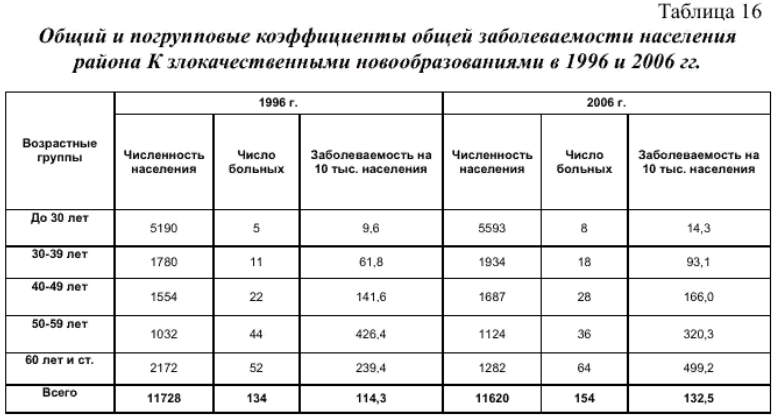 3) Рассчитаем ожидаемые числа случаев заболеваний ЗНО в районе «К» в 2006 г., исходя из стандарта возрастного состава населения, обычной пропорцией и занесем в таблицу (Табл.17). Порядок расчета следующий. Если заболеваемость в 2006 г. в возрастной группе до 30 лет составила 14,3 случая на 10000 населения, то если бы численность этой возрастной группы была 5190 человек, число случаев болезни составило бы – х. 10000 – 14,3 5190 – х 5190 × 14,3 / 10000 = 7,4 случая Ожидаемое число случаев заболеваний в строке «Всего» таблицы 18 получим как сумму всех ожидаемых чисел. 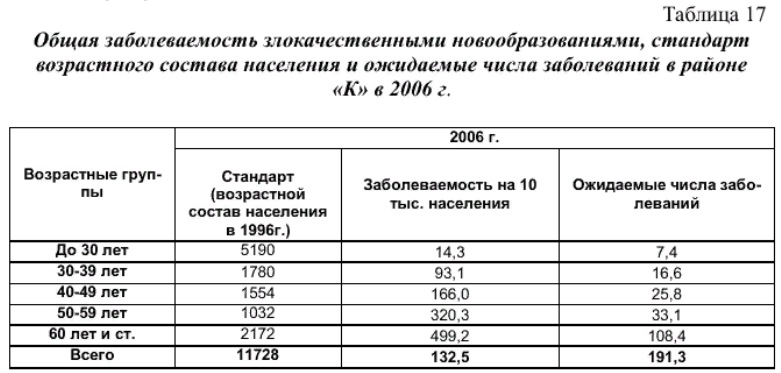 4) Рассчитаем стандартизированный показатель заболеваемости злокачест- венными новообразованиями в районе «К» в 2006 г.:  5) Проведем анализ полученных данных. В 1996 г. заболеваемость ЗНО составляла 114,3 случая на 10000 населения, а в 2006 г. - 132,5. Следовательно, произошло увеличение заболеваемости за период с 1996 по 2006 гг. Стандартизированный по возрасту показатель заболеваемости ЗНО в 2006 г. составил 163,1 случай на 10000 населения, т.е. если бы возрастной состав района «К» в 2006 г. был бы такой же как в 1996 г., то заболеваемость составила бы 163,1 случай на 10000 населения. Таким образом, можно сделать вывод, что изменения в возрастном составе не повлияли на рост заболеваемости злокачественными новообразованиями в рай-оне «К». | ||||||||||||||
