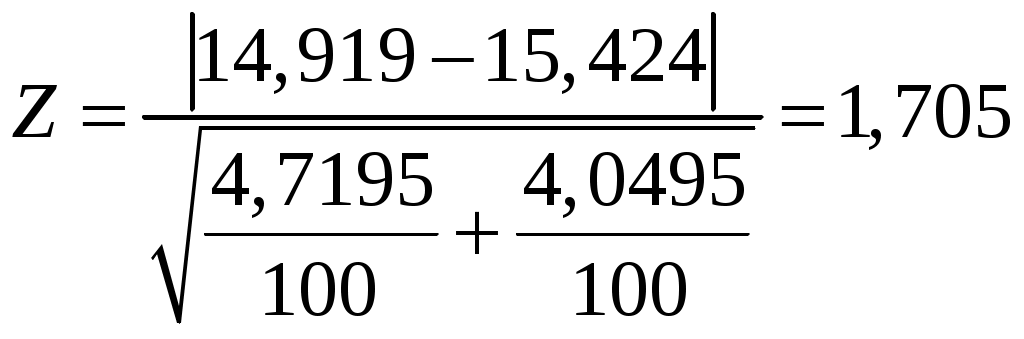2 Практическая часть 2.1 Проверка гипотезы о равенстве средних при равных дисперсиях (на примере двух выборок)
Выборка  ( )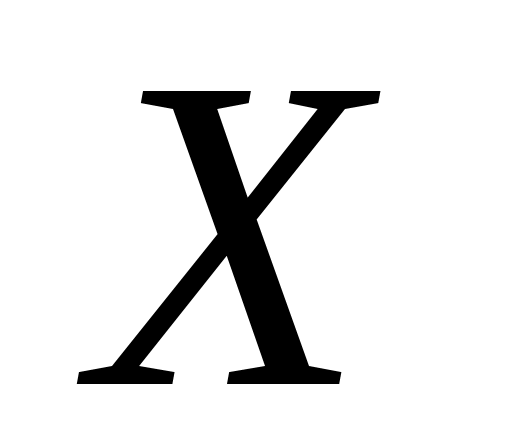
-
14,4
|
14,3
|
12,1
|
16,4
|
19,4
|
12,4
|
14,3
|
13,3
|
15,6
|
17,9
|
15,5
|
17,7
|
12
|
13,1
|
17,6
|
17,6
|
14,8
|
14,3
|
14,5
|
15,2
|
17,4
|
14,6
|
14,9
|
15,3
|
15
|
18,5
|
14
|
15,1
|
16,1
|
15,9
|
10,6
|
18,9
|
14,4
|
15,3
|
14,9
|
14,5
|
16,7
|
19,4
|
13,2
|
12,9
|
17,2
|
19,8
|
11,5
|
18,8
|
11,5
|
12,8
|
13,7
|
13,5
|
16
|
16,7
|
13,6
|
18,3
|
9,8
|
15,1
|
15,9
|
11,6
|
11,8
|
17,9
|
16,7
|
16,2
|
11,3
|
16,1
|
12,4
|
16,7
|
15,4
|
13
|
16,8
|
13,7
|
13,7
|
12,9
|
13,5
|
18,8
|
16,5
|
13,2
|
17,5
|
10,8
|
14,8
|
15,9
|
17,2
|
14,4
|
13,9
|
14
|
16,7
|
12,6
|
13,3
|
14,2
|
16,4
|
16,2
|
11,9
|
13,4
|
15,3
|
14,2
|
12,3
|
16,4
|
14,1
|
14,3
|
16,5
|
12,8
|
16,3
|
14,1
|
Выборка  ( )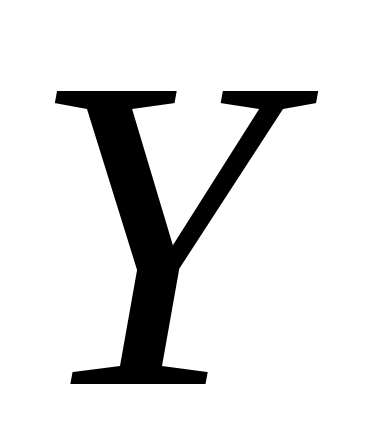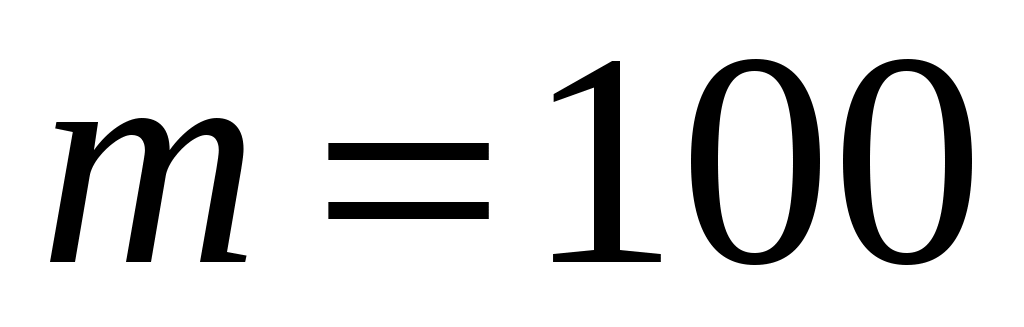
-
16,8
|
14,2
|
14,2
|
13,5
|
16,6
|
14,8
|
18
|
12,8
|
16,6
|
15,2
|
15,2
|
15,5
|
16,1
|
16,8
|
16,1
|
14,3
|
15,4
|
15,2
|
13,8
|
16,2
|
15,2
|
18,7
|
16,6
|
17,1
|
15,8
|
11
|
16,2
|
14,2
|
16,8
|
15
|
15,2
|
16,4
|
14,8
|
15,1
|
12,8
|
12,8
|
15
|
16,1
|
12,4
|
19,7
|
15,8
|
16,9
|
14,8
|
17,5
|
18,7
|
16,5
|
15,4
|
15,9
|
17
|
17,6
|
18,1
|
14
|
10,6
|
14,8
|
12,5
|
14,3
|
13,3
|
15,4
|
14,1
|
13,3
|
14
|
15,9
|
16
|
17,2
|
16,6
|
15,8
|
13,5
|
19,7
|
16,2
|
15,6
|
15
|
19,4
|
12,4
|
16,6
|
15,5
|
15,1
|
15,2
|
12,4
|
19,7
|
15,8
|
18,7
|
12,3
|
10,9
|
16
|
11,7
|
15,6
|
14,8
|
17,8
|
13,3
|
15
|
15,2
|
17,4
|
20,2
|
16,5
|
13,6
|
19,2
|
14,7
|
14,7
|
13
|
13,5
|
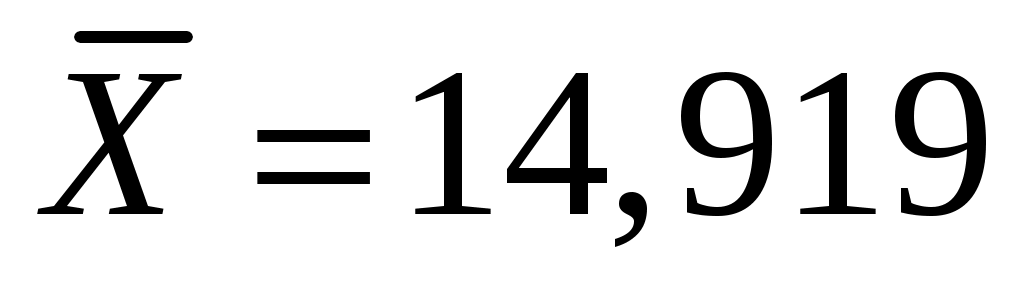
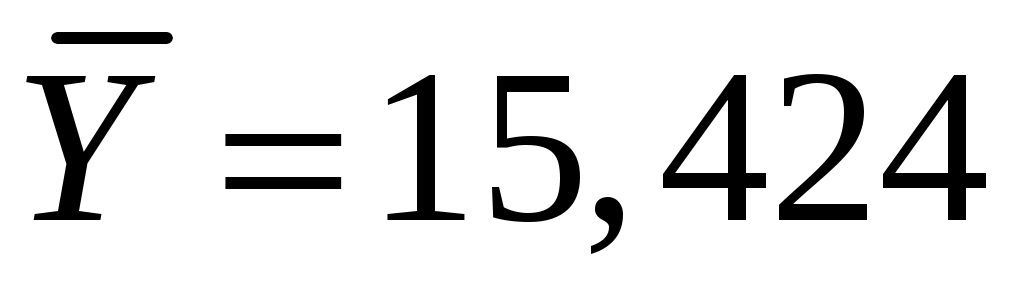
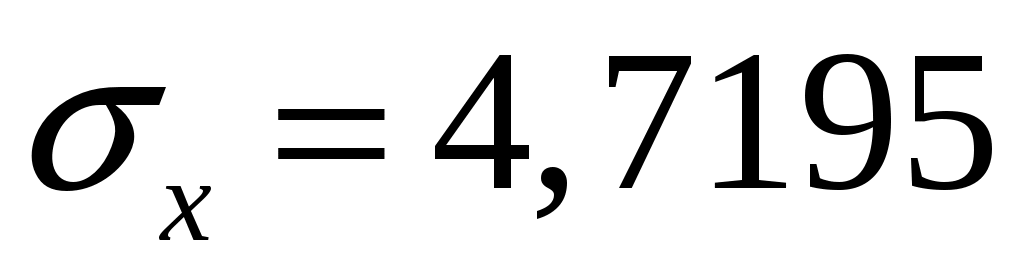
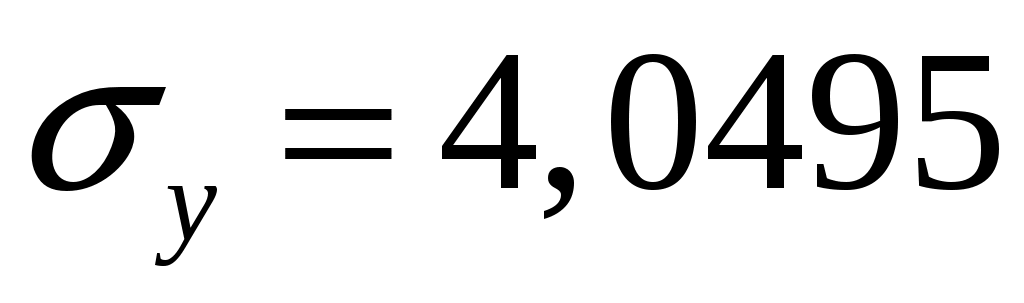
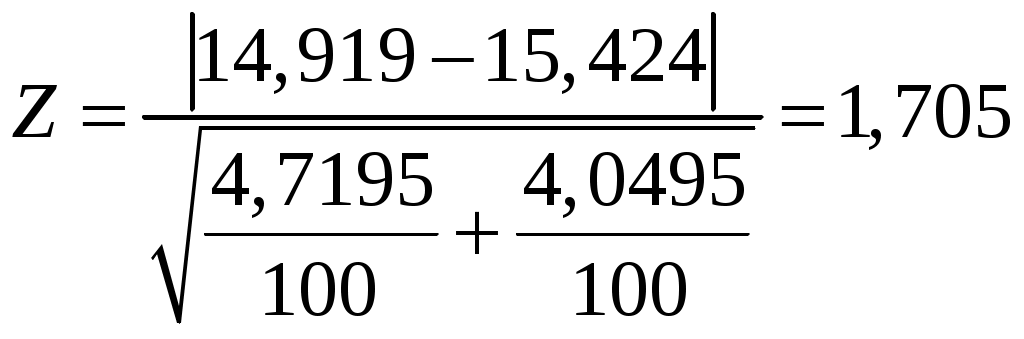
Находим правую критическую точку:
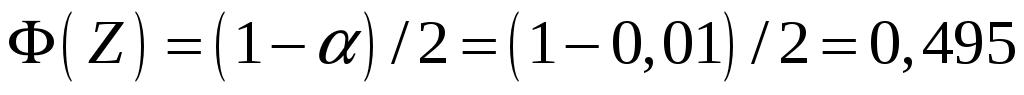
По таблице функции Лапласа находим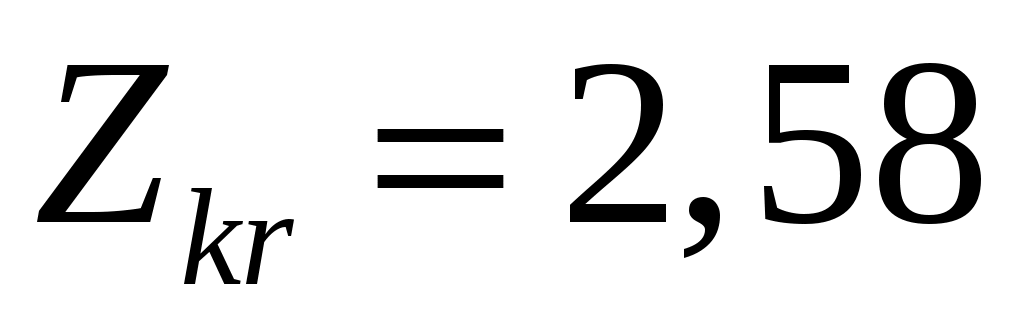 
Так как 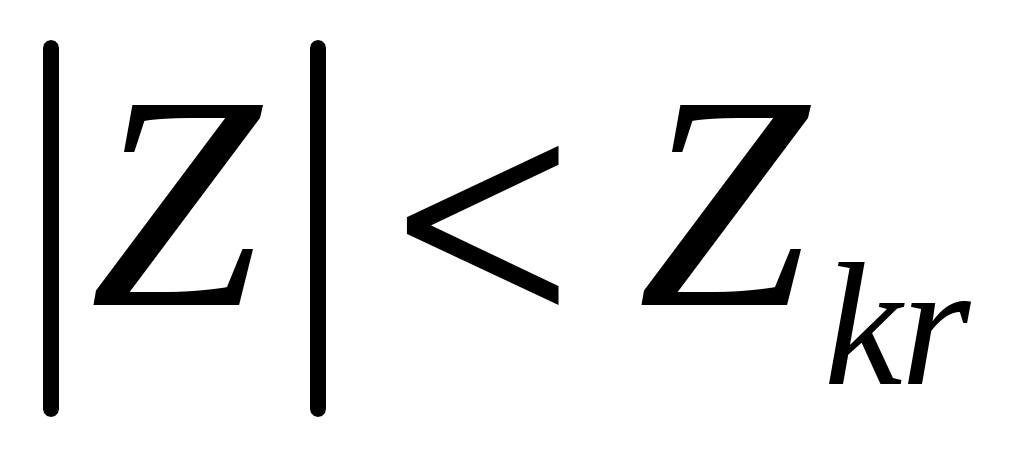 , значит гипотезу о равенстве двух средних выборок принимаем.
|
Скачать 477.5 Kb.