Методы проверки гипотез о положении и рассеивании значений+++. Методы проверки гипотез о положении и рассеивании значений параметров в биометрии

• Название: Методы проверки гипотез о положении и рассеивании значений параметров в биометрии
• Дата: 17.05.2023
• Размер: 477.5 Kb.
• Имя файла: Методы проверки гипотез о положении и рассеивании значений+++.doc
• Тип: Реферат; #1138980
• страница: 2 из 5

1 Теоретическая часть

1.1 Проверка гипотезы о равенстве средних при равных дисперсиях

Пусть из каждой из двух нормально распределенных генеральных совокупностей (с параметрами , ) и (с параметрами , ) извлечены выборки объема и соответственно. Требуется проверить нулевую гипотезу о равенстве средних значений этих генеральных совокупностей. Альтернативная гипотеза формулируется в соответствии с условиями задачи или эксперимента:

(двустороння критическая область);

(левостороння критическая область);

(правостороння критическая область).

Случай, когда дисперсии генеральных совокупностей 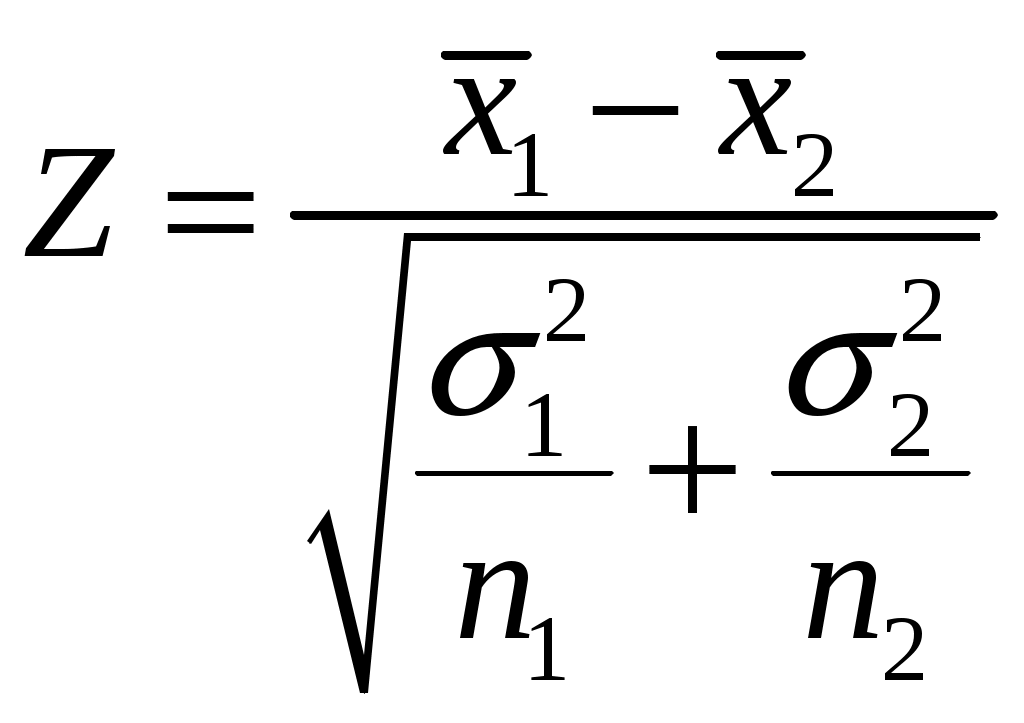и известны. В этом случае для проверки нулевой гипотезы используют случайную величину

,

где – выборочные средние первой и второй выборок соответственно. Если нулевая гипотеза справедлива, то статистика имеет нормальное распределение с математическим ожиданием, равным нулю и дисперсией, равной единице. Критическое значение выбирается в соответствии с задаваемым уровнем значимости по таблице значений функции Лапласа или стандартного нормального распределения.

Если объемы выборок достаточно велики , то случайную величину можно использовать и при неизвестных дисперсиях генеральных совокупностей, положив в выражении для : , .

Эту же статистику используют и при проверке гипотезы о равенстве вероятностей «успеха». Объемы выборок должны быть достаточно велики, чтобы биномиальное распределение можно было бы приближенно считать нормальным.

1.2 Проверка гипотезы о равенстве средних при связанных выборках

Критерий Стьюдента (t-критерий) позволяет найти вероятность того, что оба средних значения в выборке относятся к одной и той же совокупности. Данный критерий наиболее часто используется для проверки гипотезы: «Средние двух выборок относятся к одной и той же совокупности».

При использовании критерия можно выделить два случая. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух независимых, несвязанных выборок (так называемый двухвыборочный t-критерий). В этом случае есть контрольная группа и экспериментальная (опытная) группа, количество испытуемых в группах может быть различно.

Во втором случае, когда одна и та же группа объектов порождает числовой материал для проверки гипотез о средних, используется так называемый парный t-критерий. Выборки при этом называют зависимыми, связанными.

В случае связанных выборок с равным числом измерений в каждой можно использовать более простую формулу t-критерия Стьюдента.

Вычисление значения t осуществляется по формуле: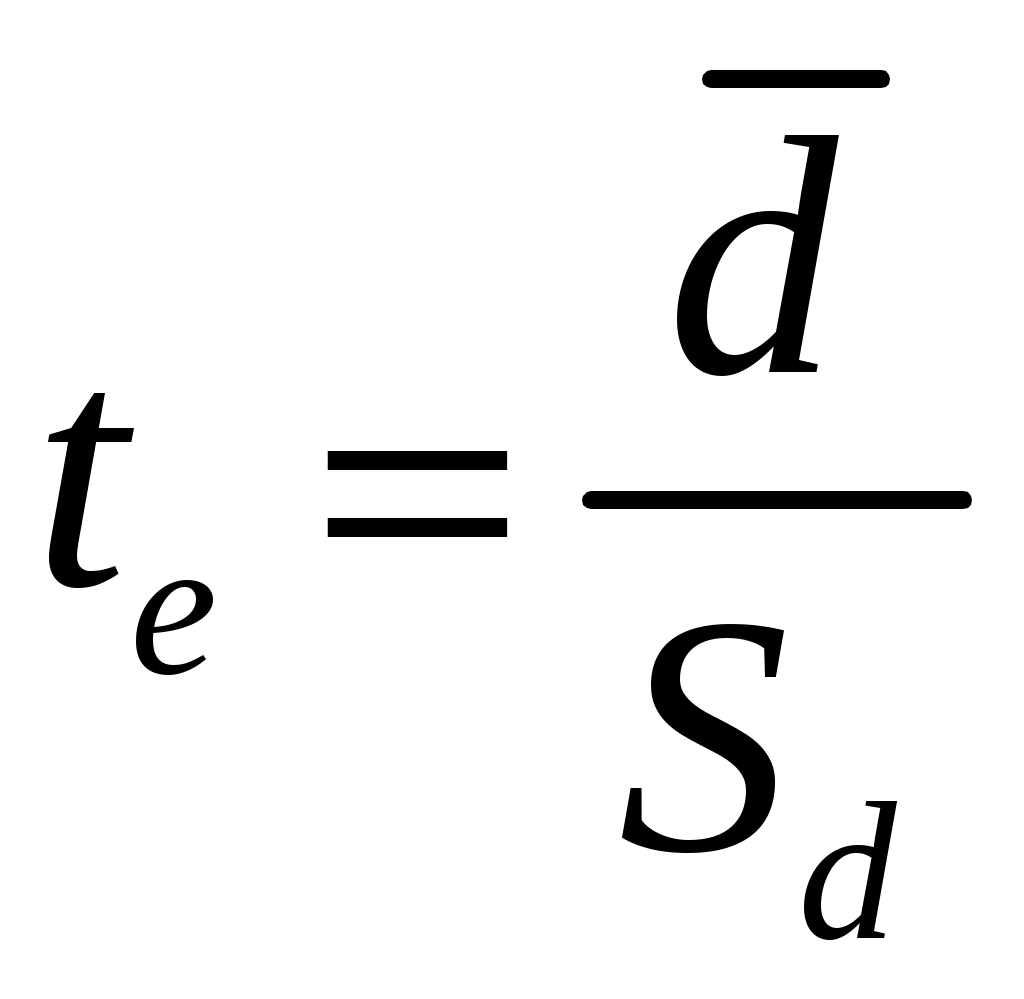

,

где 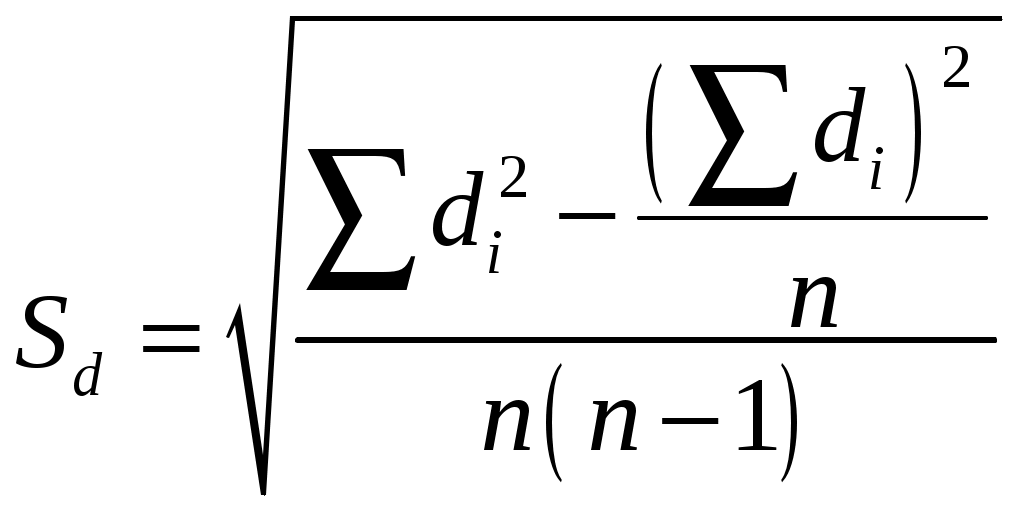– разности между соответствующими значениями переменной и переменной ; – среднее этих разностей; вычисляется по следующей формуле:

.

Число степеней свободы определяется по формуле . Если , то нулевая гипотеза принимается, в противном случае принимается альтернативная.