Методы расчета показателей надежности котельного агрегата. Методы расчета показателей надежности котельного агрегата Оглавление

• Название: Методы расчета показателей надежности котельного агрегата Оглавление
• Анкор: Методы расчета показателей надежности котельного агрегата
• Дата: 23.09.2022
• Размер: 286.32 Kb.
• Имя файла: Kursovaya_rabota_Metody_rascheta_pokazateley_nadezhnosti_kotelno.docx
• Тип: Документы; #692057

Методы расчета показателей надежности котельного агрегата

Оглавление

Введение – 1 стр.

Основная часть – 3 стр.

1. Введение в теорию надежности – 3 стр.

1.1 Историческая справка – 3 стр.

1.2 Краткие положения теории надежности – 5 стр.

1.3 Примеры того как можно получить информацию о надежности котельных агрегатов – 6 стр.

1.4 Основная используемая терминология – 8 стр.

2. Методика расчета основных показателей надежности – 13 стр.

2.1 Котельные агрегаты как сложные системы – 13 стр.

2.2 Расчет показателей безотказности – 14 стр.

2.3 Расчет показателей долговечности – 16 стр.

2.4 Расчет показателей сохраняемости – 16 стр.

2.5 Расчет показателей ремонтопригодности – 16 стр.

2.6 Расчет комплексных показателей надежности – 17 стр.

2.7 Нормирование надежности – 18 стр.

3. Математическая основа надежности котельных агрегатов – 21 стр.

3.1 Нормальное распределение случайной величины – 24 стр.

3.2 Экспоненциальное распределение случайной величины – 25 стр.

3.3 Распределение Вейбулла случайной величины – 26 стр.

Заключение – 28 стр.

Список использованной литературы – 30 стр.
Введение

Одной из причин актуальности исследования методов расчета показателей надежности котельных агрегатов является то, что без этого невозможна разработка вопросов методологии развития современной техники и, в первую очередь, анализа соответствия закономерностей развития техники законам общества и окружающей среды.

Как известно, надежность представляет собой комплексный фактор, объективно присущий всем материальным системам и дающий возможность устанавливать оптимальную меру соответствия рабочих процессов и выходных характеристик системы её функциональному назначению.

Для начала, следует понять, что же такое котельные агрегаты. Котельными агрегатами являются устройствами, имеющие топку для сжигания органического топлива в окислительной среде, где в результате экзотермических химических реакций горения образуются газообразные продукты с высокой температурой (топочные газы), теплота от которых передается другому теплоносителю (воде или водяному пару), более удобному для дальнейшего использования.

Особое положение в исследуемой теме занимают влияние надежности котельных агрегатов на общество и окружающую среду.

Второй из причин актуальности, помимо технического аспекта, является фактор социальный.

Целью данной работы является анализ методов расчета показателей надежности котельных агрегатов, обобщение материалов по данной теме и их систематизация.

Для этого решались такие задачи как анализ литературы и исторический обзор по данной теме, описание основных понятий исследования, систематизация данных.

Состояние и степень разработанности данной темы относительно невелика, среди авторов изучавших данный вопрос можно выделить: К. В. Фролов, В. Г. Пушкин, Е. Р. Ставровский, А. А. Комаров, Н. А. Северцев, П. А. Обновленский и другие.

Основная часть

1. Введение в теорию надежности

1.1 Историческая справка

Первоначальный этап начинается с начала появления первых технических устройств (это конец XIX в. (приблизительно 1880 г.)) и заканчивается с появлением электроники и автоматики, авиации и ракетно-космической техники (середина XX в.).

Уже в начале века ученые стали задумываться, как сделать любую машину неломающейся. Появилось такое понятие, как «запас» прочности. Но, увеличивая запас прочности, увеличивается и масса изделия, что не всегда приемлемо. Специалисты стали искать пути решения этой проблемы.

Основой для решения таких проблем стала теория вероятностей и математическая статистика. На базе указанных теорий уже в 30-е гг. было сформулировано понятие отказа, как превышение нагрузки над прочностью.

Теория надежности активно развиваться с развитием авиации, автоматики и электроники.

Следующим этапом, стал этап становления теории надежности (1950 – 1960). В 1950 г. военно-воздушные силы США создали группу для исследования вопросов надежности радиоэлектронного оборудования. Они установила, что главная причина поломок радиоэлектронной аппаратуры заключалась в низкой надежности ее элементов. При этом разбирались, изучали влияние различных факторов на исправную работу элементов и собрали большой статистический материал, который и явился основой теории надежности.

В 1960 – 1970 годах появляется этап классической теории надежности.

В 60-70 гг. появляется космическая техника, требующая повышенной надежности. С целью обеспечения надежности этих изделий начинают анализировать конструкцию изделий, технологию производства и условия эксплуатации.

На данном этапе было установлено, что причины поломок объектов можно обнаружить и устранить. Начинает развиваться теория диагностики сложных систем. Появляются новые стандарты по надежности объектов.

После чего наступает этап системных методов надежности (с 1970 г. по настоящее время).

На этом этапе были разработаны новые требования к надежности, заложившие основу современных систем и программ обеспечения надежности. Были разработаны типовые методики проведения мероприятий, связанных с обеспечением надежности.

Эти методики разделяются на два основных направления: первое направление относится к потенциальной надежности, которое учитывает конструктивные и технологические методы обеспечения надежности; второе направление – эксплуатационное, которое направлено на обеспечение эксплуатационной надежности.

В истории можно выделить интересные моменты, так например ярким примером поиска методов расчёта надежности является история создания ракетных комплексов Фау-1 и Фау-2 Вернером фон Брауном[1]. В лаборатории Брауна работал немецкий математик Эрик Пьеружка (Eric Pieruschka), который доказал, что надёжность ракеты равна произведению надёжности всех компонент, а не надёжности самого ненадёжного элемента, как считал Браун. Позднее вместе в Брауном в середине 50-х годов в США работал талантливый немецкий инженер Роберт Луссер (Robert Lusser), который сформулировал основные теоретические положения будущей теории надёжности. Его формула для расчета надёжности системы с последовательным соединением элементов стала известна как «Закон Луссера» (Lusser's law).

А к первым работам по расчёту надежности в Советском Союзе можно отнести статью инженера Якуба Б.М. «Показатели и методы расчета надёжности в энергетическом хозяйстве», опубликованную в журнале «Электричество», №18, 1934г., и статью профессора Сифорова В.И. «О методах расчёта надёжности работы систем, содержащих большое число элементов» (Известия Академии наук СССР. Отделение технических наук. №6, 1954г.) Независимо от закрытых работ немецких ученых, в указанных статьях надёжность систем с последовательным соединением рассчитывалась как произведение надёжности элементов, [1, 5, 6, 7].
1.2 Краткие положения теории надежности

Надежность характеризует качество технического устройства. Которое в свою очередь представляет собой совокупность свойств, определяющие пригодность объекта к применению по назначению, и его потребительские свойства. Надежность как качество является комплексным свойством, в которое входит способности выполнять определённые функции, не изменяя свои основные характеристики в заданных границах. Показателями надежности являются безотказность, долговечность, ремонтопригодность и сохранность.

Теория надежности изучает причины, которыми вызываются отказы объектов, изучение закономерностей которым они подчиняются, разработка способов количественного определения надежности, методологии расчётов, испытаний, разработка путей и средств повышения надежности.

Объектом исследования теории надежности является техническое устройство: устройство в целом или его отдельные детали.

При этом существует общая теория надежности, состоящей из составных частей, и прикладные теории надежности.

Составные части общей теории надежности:

1. Математическая теория надежности, изучает математические закономерности, которым подчиняются отказы, методы количественного измерения надежности, и инженерные расчеты показателей надежности.

2. Статистическая теория надежности, представляет собой обработку статистической информации о надежности. Статистические характеристики надежности и закономерности отказов.

3. Физическая теория надежности, исследует физико-химические процессы, физических причин отказов, влияния старения и прочности материалов на надежность.

Прикладные теории надежности разрабатываются применительно в конкретной области техники к объектам этой области. Например, существует теория надежности систем управления, теория надежности электронных устройств, теория надежности машин и другие, [1, 5, 6, 7, 8, 13, 14, 15, 17, 18].
1.3 Примеры того как можно получить информацию о надежности котельных агрегатов

Составной частью работ обеспечивающих и повышающих надежность котельных агрегатов являются испытания на надежность. В зависимости от контролируемых или оцениваемых свойств, образующих надежность, могут состоять из испытаний на безотказность, долговечность, ремонтопригодность и сохраняемость. Например, ресурсные испытания являются испытаниями на долговечность.

С помощью методов математической статистики проводится планирование и обработка результатов испытаний, при этом должно происходить оценивание значений показателей надежности с определенной точностью и достоверностью. Иными словами должна быть задана определенная относительная погрешность и уровень достоверности. Точно такие же требования должны быть и к контрольным испытаниям. При ускорении испытаний необходимо не допустить снижение точности и достоверности оценок.

Сбором информации об отказах котельных агрегатов могут заниматься:

– организации-разработчики машины;

– предприятия-изготовители машины;

– эксплуатационные и ремонтные предприятия.

Организации-разработчики (проектные институты) осуществляют сбор и обработку информации о надежности опытных образцов котельных агрегатов путем проведения специальных испытаний. Предприятия-изготовители (машиностроительные заводы) осуществляют сбор и обработку первичной информации о надежности серийно изготовляемой продукции и анализ причин отказов котельных агрегатов. Сбор информации они ведут на основе проведения специальных заводских и эксплуатационных испытаний. Эксплуатационные и ремонтные организации собирают первичную информацию о надежности котельных агрегатов в эксплуатации. Основным источником получения информации о надежности, являются испытания. Различают следующие виды испытаний:

Заводские (ресурсные) испытания – испытания опытных или первых серийных образцов. Эти испытания бывают:

а) доводочные;

б) на пригодность к серийному производству;

в) контрольные;

г) приемосдаточные;

д) исследовательские.

Цель доводочных испытаний – оценить влияние на надежность изменений, вносимых при доводке конструкции и технологии производства. Испытания на пригодность к серийному производству определяют допустимость к серийному производству котельных агрегатов по их надежности.

Контрольными испытаниями проверяют обеспечение установленных норм надежности серийно выпускаемых котельных агрегатов.

Приемосдаточные испытания определяют соответствие данной партии котельных агрегатов требованиям технических условий и возможность ее приемки.

Цель исследовательских испытаний – определить границы выносливости котельных агрегатов, установить закон распределения ресурсов, изучить динамику процесса изнашивания, сравнить ресурсы котельных агрегатов.

Сбор информации о надежности котельных агрегатов проводят в соответствии с требованиями отраслевой нормативно-технической документации.

Информация о надежности котельных агрегатов должна удовлетворять следующим требованиям:

1) полнота информации, под которой понимается наличие всех сведений, необходимых для проведения оценки и анализа надежности;

2) достоверность информации, т.е. все сообщения об отказах должны быть точными;

3) своевременность информации позволяет быстрее устранять причины отказов и принимать меры по устранению выявленных недостатков;

4) непрерывность информации позволяет сопоставлять результаты расчетов, полученные в первый и последующий периоды эксплуатации и избавляет от ошибок [1, 5, 6, 7, 8, 9, 13].
1.4 Основная используемая терминология

Для изучения и понимания методики расчета показателей надежности котельных агрегатов, необходимо знать основную терминологию.

Ниже приведены основные термины и понятия, [1, 5-9, 13-15, 17-21].

Надежность это свойство сохранять во времени в принятых границах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, хранения и транспортирования. Надежность представляет собой комплексное свойство котельного агрегата, и в зависимости от условий использования может включать в себя такие показатели: безотказность, долговечность, ремонтопригодность и сохраняемость или сочетания этих свойств.

Показатель надежности это количественная характеристика одного или нескольких свойств, образующих надежность котельного агрегата.

Единичный показатель надежности – характеризует одно из свойств, образующих надежность котельного агрегата.

Комплексный показатель надежности – характеризует совокупность свойств, образующих надежность котельного агрегата.

Расчетный показатель надежности – показатель надежности, определяемый расчетным методом.

Экспериментальный показатель надежности – показатель надежности, точечная или интервальная оценка которого определяется по данным испытаний.

Эксплуатационный показатель надежности – показатель надежности, точечная или интервальная оценка которого определяется по данным эксплуатации.

Экстраполированный показатель надежности – показатель надежности, точечная или интервальная оценка которого определяется на основании результатов расчетов, испытаний и (или) эксплуатационных данных путем экстраполирования на другую продолжительность эксплуатации и другие условия эксплуатации.

Расчетный метод определения надежности – метод, основанный на вычислении показателей надежности по справочным данным о надежности компонентов и комплектующих элементов, по данным о надежности аналогов, по данным о свойствах материалов и другой информации, имеющейся к моменту оценки надежности.

Расчетно-экспериментальный метод определения надежности – метод, при котором показатели надежности всех или некоторых составных частей котельного агрегата определяют по результатам испытаний и (или) эксплуатации, а показатели надежности объекта рассчитывают по математической модели.

Экспериментальный метод определения надежности – основывается статистической обработке данных, полученных в результате испытаний или эксплуатации котельного агрегата.

Нормируемый показатель надежности – показатель надежности, значение которого регламентировано нормативно-технической и (или) конструкторской (проектной) документацией на котельный агрегат.

Безотказность – свойство котельного агрегата сохранять непрерывно работоспособное состояние в течение времени или наработки.

Вероятность безотказной работы – возможность того, что в границах заданной наработки отказ котельного агрегата по производительности не произойдет.

Средняя наработка до отказа – математическое ожидание наработки котельного агрегата до первого отказа.

Плотность вероятности отказа (частота отказов) – отношение числа отказавших котельных агрегатов в единицу времени к первоначальному числу находящихся под наблюдением при условии, что отказавшие котельные агрегаты не восстанавливаются и не заменяются новыми.

Интенсивность отказов – условная плотность вероятности возникновения отказа котельного агрегата, определяемая при условии, что до рассматриваемого момента времени отказ не возник. То есть это отношение числа отказавших котельных агрегатов в единицу времени к среднему числу работающих безотказно за данный промежуток времени при условии, что отказавшие котельные агрегаты не восстанавливаются и не заменяются новыми.

Долговечность – свойство котельного агрегата сохранять работоспособное состояние до наступления граничного состояния при установленной системе технического обслуживания и ремонта.

Средний ресурс – математическое ожидание ресурса.

Гамма-процентный ресурс – наработка, в течение которой котельный агрегат не достигнет граничного состояния с заданной вероятностью, выраженной в процентах.

Средний срок службы – математическое ожидание срока службы.

Ремонтопригодность приспособленность к поддержанию и восстановлению работоспособного состояния при помощи технического обслуживания и ремонта.

Время восстановления – это продолжительность восстановления работоспособного состояния котельного агрегата. Определяется как сумма времени, затраченное на отыскание и устранение отказа, и на проведение необходимых отладок и проверок, для того чтобы удостовериться в восстановлении работоспособности котельного агрегата.

Среднее время восстановления – математическое ожидание времени восстановления котельного агрегата.

Вероятность восстановления работоспособного состояния – возможность того, что время восстановления работоспособного состояния котельного агрегата не превысит заданное значение.

Сохраняемость – является свойством сохранения в заданных границах значения параметров, характеризующих способность объекта выполнять свои функции, в течение и после хранения и (или) транспортирования.

Средний срок сохраняемости – представляет собой математическое ожидание срока сохраняемости.

Гамма-процентный срок сохраняемости – календарная продолжительность хранения и (или) транспортирования котельного агрегата, в течение и после которой показатели безотказности, долговечности и ремонтопригодности котельного агрегата не выйдут за определенные границы с вероятностью γ, %.

Коэффициент готовности – возможность того, что котельный агрегат будет работоспособным в любой момент времени, за исключением планируемых периодов, в которых не предусматривается применение котельного агрегата.

Коэффициент технического использования – отношение математического ожидания суммарного времени пребывания котельного агрегата в работоспособном состоянии за какой-нибудь период эксплуатации к математическому ожиданию суммарного времени пребывания котельного агрегата в работоспособном состоянии и простоев, объясняемых техническим обслуживанием, ремонтом за тот же период использования.

Случайная величина – величина, в результате опыта принимающее одно, заранее неизвестное значение, которое зависит от случайных причин.

2. Методика расчета основных показателей надежности

2.1 Котельные агрегаты как сложные системы

Котельный агрегат можно принять за сложную систему, предназначенный для выполнения заданных функций, который может быть расчленен на элементы, каждый из которых также выполняет определенные функции и находится во взаимодействии с другими элементами системы.

Понятие сложной системы условно. Оно может применяться как к отдельным узлам и механизмам, так и к самому котельному агрегату.

1. Котельный агрегат состоит из большого количества элементов, каждый из которых имеет свои характеристики надежности.

Котельный агрегат может состоять из сотен деталей, каждая из которых имеет свои характеристики надежности.

2. Не все элементы одинаково влияют на надежность котельного агрегата. Многие из них влияют лишь на эффективность ее работы, а не на ее отказ. Степень влияния каждого элемента на надежность котельного агрегата зависит от многих факторов, таких как: назначение элемента, характер взаимодействия элемента с другими элементами котельного агрегата, структура котельного агрегата, вид соединений элементов между собой.

3. Каждый экземпляр котельного агрегата имеет индивидуальные черты, так как незначительные вариации свойств отдельных элементов котельного агрегата сказываются на выходных параметрах всего агрегата. Чем сложнее котельный агрегат, тем большими индивидуальными особенностями она обладает.

При анализе надежности сложных котельных агрегатов их разбивают на элементы (звенья) с тем, чтобы вначале рассмотреть параметры и характеристики элементов, а затем оценить работоспособность всего котельного агрегата.

Теоретически любую сложную систему можно условно разделить на большое число элементов, понимая под элементом узел или деталь.

Под элементом будем понимать составную часть сложной системы, которая может характеризоваться самостоятельными входными и выходными параметрами, [5-9].
2.2 Расчет показателей безотказности

Здесь и далее, под объектом следует понимать котельный агрегат.

Для оценки безотказности применяют следующие показатели, [1, 5, 6, 8, 9, 13-15, 17- 21]:

1 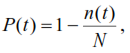. Вероятность безотказной работы, которая изменяется от 0 до 1, рассчитывается по формуле (1):

(1)

где N – число объектов, работоспособных в начальный момент времени; n(t) – число объектов, отказавших на момент t от начала испытаний или эксплуатации.

Вероятность безотказной работы Р объекта связана с вероятностью отказа F следующим соотношением (2):

(2)

Возможность безотказной работы уменьшается с увеличением времени работы или наработки объекта. Зависимости вероятности безотказной работы P(t) и вероятности отказа F(t) от наработки t представлены на рисунке 1.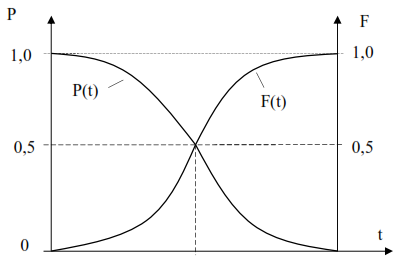



Рисунок 1 – Зависимости вероятности безотказной работы и вероятности отказа от наработки: Р – вероятность безотказной работы; F – вероятность отказа.

В начальный момент времени для работоспособного объекта возможность его безотказной работы равна единице (100 %). По мере работы объекта эта вероятность снижается и стремится к нулю. Возможность возникновения отказа объекта, наоборот, возрастает с увеличением срока эксплуатации или наработки.

2 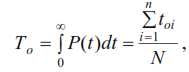. Средняя наработка до отказа (среднее время безотказной работы) и средняя наработка на отказ. Этот показатель часто называют средним временем безотказной работы. Определяется по формуле (3):

(3)

где t_i – наработка до отказа i-го объекта; N – число объектов.

Средняя наработка на отказ – математическое ожидание времени i между соседними отказами объекта.

3 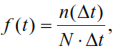. Плотность вероятности отказа определяется по формуле (4):

(4)

где n(Δt) − число отказов в рассматриваемом интервале наработки; N − общее число объектов, находящихся под наблюдением; Δt – величина рассматриваемого интервала наработки.

4 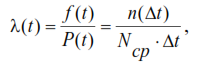. Интенсивность отказов оценивают по следующей формуле (5):

(5)
г де f(t) – частота отказов; P(t) – вероятность безотказной работы; n(Δt) – число отказавших объектов за время от t до t + Δt; Δt – рассматриваемый интервал наработки; N_ср – среднее число безотказно работающих объектов определяемое по формуле (6):

(6)

где N(t) − число безотказно работающих объектов в начале рассматриваемого интервала наработки; N(t + Δt) − число безотказно работающих объектов в конце интервала наработки.

2.3 Расчет показателей долговечности

1 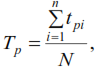. Средний ресурс определяется по формуле (7), [1, 5, 6, 8, 9, 13-15, 17- 21]:

(7)
где t_pi– ресурс i-го объекта; N – число объектов.

2 . Га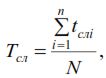мма-процентный ресурс, γ – заданная вероятность %, для расчета показателя используется формула вероятности (8), [1, 5, 6, 8, 9, 13-15, 17- 21]:

(8)

3 . Средний срок службы определяется по формуле (9), [1, 5, 6, 8, 9, 13-15, 17- 21]:

(9)

где t_слi – срок службы i-го объекта.

4. Гамма-процентный срок службы – календарная продолжительность эксплуатации, в течение которой объект не достигает граничного состояния с вероятностью γ, выраженной в процентах.
2.4 Расчет показателей сохраняемости

Для оценки сохраняемости применяют следующие показатели, [1, 5, 6, 8, 9, 13-15, 17- 21]:

1. Средний срок сохраняемости.

2. Гамма-процентный срок сохраняемости.

Показатели сохраняемости по сути своей соответствуют показателям долговечности и определяются по тем же формулам.
2.5 Расчет показателей ремонтопригодности

Для оценки ремонтопригодности применяют следующие показатели, [1, 5, 6, 8, 9, 13-15, 17- 21]:

1 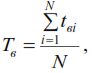. Среднее время восстановления определяется по формуле (10):

(10)
где t_вi – время восстановления i-го отказа объекта; N – число отказов за заданный срок испытаний или эксплуатации.

2. Вероятность восстановления. Подчиняется экспоненциальному закону распределения, определяется по формуле (11):

(11)

где λ – интенсивность отказов (принимается постоянной).
2.6 Расчет комплексных показателей надежности

Каждый из описанных выше показателей позволяет оценить лишь одну из сторон надежности – одно из свойств надежности объекта.

Для более полной оценки надежности используют комплексные показатели, позволяющие одновременно оценить несколько важнейших свойств объекта, [1, 5, 6, 8, 9, 13-15, 17- 21].

1. Коэффициент готовности К_г, определяется по формуле (12):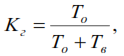



(12)

где Т_о – среднее значение наработки на отказ; Т_в – среднее время восстановления объекта после отказа.

2 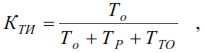. Коэффициент технического использования, определяется по формуле (13):

(13)
где Т_Р, Т_ТО – суммарная продолжительность простоев объекта в ремонте и техническом обслуживании.
2.7 Нормирование надежности

С целью создания высоконадежных объектов необходимо нормирование надежности – установление номенклатуры и количественных значений основных показателей надежности элементов объекта.

Номенклатуру показателей надежности выбирают в зависимости от класса объектов, режимов эксплуатации, характера отказов и их последствий.

Выбор показателей надежности может определяться заказчиком.

Все объекты подразделяются на следующие классы:

– неремонтируемые и невосстанавливаемые объекты общего назначения. Составные части объектов, невосстанавливаемые на месте эксплуатации и не подлежащие ремонту, а также невосстанавливаемые самостоятельного функционального назначения;

– восстанавливаемые объекты, подвергающиеся плановым техническим обслуживаниям, текущему и среднему ремонту, а также объекты, подвергающиеся капитальному ремонту;

– объекты, предназначенные для выполнения кратковременных разовых или периодических заданий.

Режимы эксплуатации изделий могут быть следующими:

– непрерывными, работа непрерывна в течение определенного времени;

– циклическими, когда работа задается периодичностью в течение определенного времени;

– оперативными, когда неопределенный период простоя сменяется периодом работы заданной продолжительности.

Обычно нормируют вероятность безотказной работы P(t) с оценкой ресурса Т_р, в течение которого она регламентируется. Значение Т_р должно быть согласовано со структурой и периодичностью ремонтных работ и технического обслуживания, а допустимая вероятность безотказной работы является мерой опасности последствий отказа.

Пример градации по классам надежности представлен на рисунке 2.


Рисунок 2 – Примеры градаций по классам надежности

Значения P(t) заданы для определенного периода эксплуатации Т_р при условии строгой регламентации и выполнения режимов работы и условий эксплуатации.

В нулевой класс входят малоответственные детали и узлы, отказ которых остается практически без последствий.

Классы с первого по четвертый характеризуются повышенными требованиями к безотказной работе (номер класса соответствует числу девяток после запятой).

В пятый класс включаются высоконадежные объекты, отказ которых в заданный период недопустим.

При доказательстве численных значений нормируемых показателей надежности руководствуются принципом оптимального распределения расходов на повышение надежности, техническое обслуживание и ремонт, а значения нормируемых показателей надежности учитываются, например, при назначении гарантийного срока эксплуатации, являющимися технико-экономическими характеристиками объекта и не относятся к показателям надежности. Гарантийные сроки, показатели надежности и цена объекта должны быть увязаны между собой.

Продолжительность гарантийного срока эксплуатации (гарантийной наработки, гарантийного срока хранения) должна быть таокй чтобы можно было выявить и ликвидировать скрытые дефекты, и обуславливается соглашением между потребителем и поставщиком.

Надежность объектов нарушается возникающими отказами. Отказы рассматривают как случайные события. Для количественной оценки надежности используются методы теории вероятности и математической статистики.

Показатели надежности могут определяться:

– аналитическим путем на основе математической модели – математического определения надежности;

– в результате обработки опытных данных – статистическое определение показателя надежности.

Момент возникновения отказа, частота возникновения отказов величины случайные. Поэтому базовыми методами для теории надежности являются методы теории вероятности и математической статистики, [1, 5, 6, 8, 9, 13-15, 17- 21].

3. Математическая основа надежности котельных агрегатов

Случайные величины могут быть дискретными и непрерывными.

Как известно из теории вероятности и математической статистики, общими характеристиками случайных величин являются [1-5, 7-18]:

1 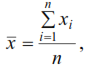. Среднее арифметическое значение, определяется по формуле (14):

(14)

где x_i – реализация случайной величины в каждом наблюдении; n – число наблюдений.

2. Размах. Понятие размаха в теории статистики используется в качестве меры рассеивания случайной величины, определяется по формуле (15):

( 15)

где x_max – максимальное значение случайной величины; x_min – минимальное значение случайной величины.

3. Среднее квадратическое отклонение является также мерой рассеивания случайной величины, определяется по формуле (16):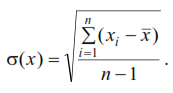




(16)
4 . Коэффициент вариации также характеризует рассеивание случайной величины с учетом средней величины. Коэффициент вариации определяется по формуле (17):

(17)

Различают случайные величины с малой вариацией (V≤0,1), средней вариацией (0,1) и большой вариацией (V>0,33). Если коэффициент вариации V<0,33, то случайная величина подчиняется нормальному закону распределения. Если коэффициент вариации 0,33, то – распределению Вейбулла. Если коэффициент вариации V=1, то – равновероятному распределению.

В теории и практике надежности чаще всего используются следующие законы распределения: нормальный, логарифмически нормальный, Вейбулла, экспоненциальный.

Законом распределения случайной величины называется соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Для характеристики закона распределения случайной величины используются следующие функции.

Функция распределения случайной величины может быть представлена графиком, рисунок 3.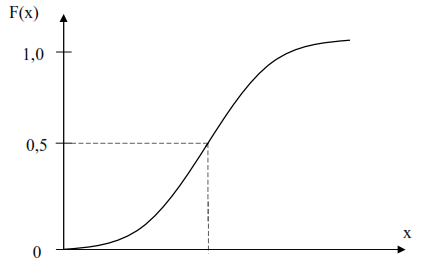



Рисунок 3 – Функция распределения случайной величины

1. Функция распределения случайной величины – функция F(х), определяющая возможность того, что случайная величина Х в результате испытаний примет значение меньше или равное х, уравнение (18):

( 18)

2. Плотность распределения вероятностей случайной величины, уравнение (19):

( 19)

Плотность вероятности характеризует возможность того, что случайная величина примет конкретное значение x, рисунок 4.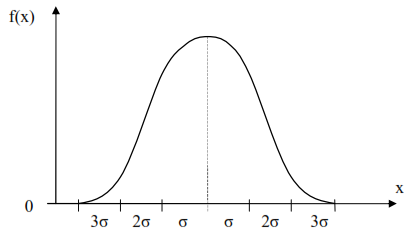



Рисунок 4 – Плотность распределения вероятностей (нормальный закон распределения)

Экспериментальной оценкой плотности вероятности случайной величины является гистограмма распределения случайной величины, рисунок 5.

Гистограмма показывает зависимость количества наблюдаемых значений случайной величины в определенном интервале значений от границ этих интервалов. По гистограмме можно приближенно судить о плотности распределения случайной величины.

При построении гистограммы в выборке случайной величины x из n значений определяют наибольшее x_max и наименьшее x значения.

Диапазон изменения величины R разбивают на x_min одинаковых интервалов. Затем подсчитывают число наблюдаемых значений случайной величины n_i, попадающих в каждый i-й интервал.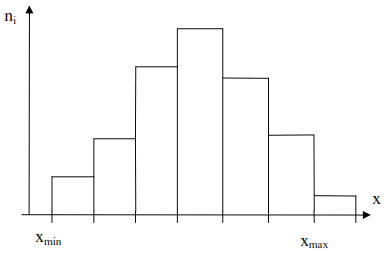



Рисунок 5 – Гистограмма распределения случайной величины

3.1 Нормальное распределение случайной величины

Закон нормального распределения является основным в математической статистике. Он формируется тогда, когда на протяжении исследуемого процесса на его результат влияет сравнительно большое число независимых факторов, каждое из которых, в отдельности, оказывает лишь незначительное действие по сравнению с суммарным влияниям всех остальных, [1-5, 7-18].

Плотность распределения (частота отказов) при нормальном законе определяется по формуле (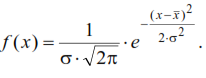20):

( 20)

Ф 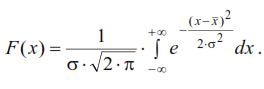ункция распределения (вероятность отказа) данного закона находится по формуле (21):

(21)
Функция надежности (вероятность безотказной работы) противоположна функции распределения, определяется по формуле (22):

( 2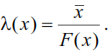2)

И нтенсивность отказов вычисляется по формуле (23):

(23)

Графики основных характеристик надежности при нормальном законе приведены на рисунке 6.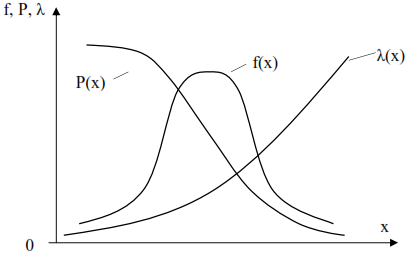



Рисунок 6 – Характеристики надежности котельных агрегатов при нормальном законе распределения

3.2 Экспоненциальное распределение случайной величины

Закон экспоненциального распределения нашел широкое применение, особенно в технике. Основной отличительной чертой этого закона является то, что возможность безотказной работы не зависит от того, сколько проработало изделие с начала эксплуатации. Закон не учитывает постепенного изменения параметров технического состояния, а рассматривает так называемые «нестареющие» элементы и их отказы. Как правило, данный закон описывает надежность работы объекта в период его нормальной эксплуатации, когда постепенные отказы еще не проявляются и надежность характеризуется только внезапными отказами. Эти отказы вызываются неблагоприятным сочетанием различных факторов и поэтому имеют постоянную интенсивность λ, [1-5, 7-18].

Экспоненциальное распределение часто называют основным законом надежности.

Плотность распределения (частота отказов) при экспоненциальном законе определяется по формуле (24):

( 24)

Вероятность безотказной работы при экспоненциальном законе выражается формулой (25):

( 25)

где λ – интенсивность отказов.

Интенсивность отказов для экспоненциального распределения является постоянной величиной.

Наработка на отказ находится по формуле (26):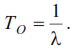

( 26)
П ри экспоненциальном законе среднеквадратичное отклонение и коэффициент вариации вычисляются следующим образом, формула (27-28):

(27)




(28)

Графики основных характеристик надежности при экспоненциальном законе приведены на рисунке 7.



Рисунок 7 – Характеристика надежности объектов при экспоненциальном законе
3.3 Распределение Вейбулла случайной величины

Распределение Вейбулла является универсальным, так как при изменении параметров оно может описывать практически любые процессы: нормального распределения, логарифмически нормального, экспоненциального, [1-5, 7-18].

Плотность распределения (частота отказов) при распределении Вейбулла определяется по формуле (29):

( 29)

где λ – параметр масштаба; α – параметр формы.

В ероятность безотказной работы при законе распределения Вейбулла выражается формулой (30):

(30)

Интенсивность отказов определяется по формуле (31):

( 31)

На рисунке 8 изображены графики надежности при распределении Вейбулла.



Рисунок 8 – Характеристика надежности котельных агрегатов при законе распределения Вейбулла (λ = 1; α = 2)

Заключение

Однако долгое время надежность не измерялась количественно, что значительно затрудняло её объективную оценку. Для оценки надежности использовались такие понятия, как высокая надежность, низкая надежность и другие качественные определения.

Увеличивающаяся сложность технических устройств, в том числе котельных агрегатов, возрастающая ответственность функций, выполняемых техническими системами, повышение требований к их качеству и условиям их работы, возросшая роль автоматизации управления техническими объектами – основные факторы, определившие главное направление в развитии науки о надежности.

Котельные агрегаты становятся все более сложными. Если не принимать специальных мер по обеспечению надежности, то любой котельный агрегат практически окажется неработоспособным.

Важность понимания принципов теории надежности, и применение ее относительно котельных агрегатов, указал академик А. И. Берг, говоря что теория надежности устанавливает закономерности возникновения отказов и восстановления работоспособности системы и её элементов, рассматривает влияние внешних и внутренних воздействий на процессы в системах, при этом создает основы расчета надежности и предсказания отказов, изыскивает способы повышения надежности.

Теория надежности тесно связана математикой, значит одной теории надежности недостаточно: с одной стороны математический аппарат широко используется для решения задач надежности технических систем, с другой стороны практика решения проблем надежности ориентирует и стимулирует развитие самой математики.

Обеспечение надежности котельного оборудования главная инженерная задача, потому что тепловая энергия – необходимое условие жизнедеятельности человека и создания благоприятных условий его быта. Надежность теплоснабжения населения и различных отраслей промышленности, которая в свою очередь обеспечивается надежной работой всех иерархических уровней системы: магистральными тепловыми сетями, квартальными сетями, тепловыми пунктами потребителей, и в том числе надежной работой котельного оборудования.

Котельные агрегаты относятся к устройствам, обслуживающим человека, их отказ влечет недопустимые для него изменения окружающей среды.

Решение вопросов надежности должно осуществляться на всех стадиях жизненного цикла, от проектирования и создания, производства, до эксплуатации, использования и утилизации.

Надежность связана с эффективностью (например, с экономической эффективностью) котельных агрегатов. Недостаточная надежность устройств имеет следствием:

– снижение производительности из-за простоев вследствие поломок;

– снижение качества результатов использования технического устройства из-за ухудшения его технических характеристик вследствие неисправностей;

– затраты на ремонты котельного агрегата;

– потеря регулярности получения результата;

– снижение уровня безопасности использования котельного агрегата.

В процессе исследования были решены задачи: анализ литературы и исторический обзор по данной теме, описание основных понятий исследования, систематизация данных.

В данной работе достаточно подробно рассмотрена и приведена методика расчета показателей надежности котельных агрегатов.

Таким образом, поставленная цель исследования достигнута.

Список использованной литературы

1. Ананьин А. Д. Диагностика и техническое обслуживание машин: учебник для студентов высш. учеб заведений / А. Д. Ананьин, В. М. Михлин, И. И. Габитов. – М.: Издательский центр «Академия», 2008. – 432 с.

2. Андронов А. М., Копытов Е. А., Гринглаз Л. Я. Теория вероятностей и математическая статистика: Учебник для вузов. – СПб.: Питер, 2004. – 461 с.

3. Абрамовиц М., Стиган И. Справочник по специальным функциям. - М.: Наука, 1979. – 832 с.

4. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 1998. – 404 с.

5. Зорин В. А. Основы работоспособности технических систем: Учебник / В.А. Зорин. – М.: ООО «Магистр-Пресс», 2005. – 536 с.

6. Иванов В. И. Техническая диагностика строительных, дорожных и коммунальных машин: учебное пособие / В. И. Иванов, В. Н. Кузнецова, Р. Ф. Салихов и др. – Омск: Изд-во СибАДИ, 2006. – Ч. 1. Теоретические основы технической диагностики СДКМ. – 132 с.

7. Каштанов В. А. Теория надежности сложных систем /В. А. Каштанов, А. И. Медведев. – 2-е изд, перераб. – М.: ФИЗМАТЛИТ, 2010. – 608 с.

8. Кучер В. Я. Основы технической диагностики и теории надежности:

Письменные лекции. – СПб.: СЗТУ, 2004. – 48 с. 5. Основы работоспособности технических систем: методическое пособие / сост.: Р.В. Абаимов, П.А. Малащук. – Сыктывкар: СЛИ, 2004. – 80 с.

9. Кокушин Н. Н. Основы теории надежности: учебное пособие / Н. Н. Кокушин, А. А. Тихонов, С. Г. Петров. – СПб.; ГОУВПО СПбГТУРП., 2011. – 77 с. [1-5, 7-18]

10. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. – М.: Наука, 1973. – 830 с.

11. Пустыльник Е. И. Статистические методы анализа и обработки наблюдений. – М.: Наука, 1968. – 228 с.

12. Севастьянов Б. А. Курс теории вероятностей и математической статистики – М.: Наука, 1982. – 256 с.

13. Токарев А. Н. Основы теории надежности и диагностика: учебник для студентов автотранспортных специальностей / Барнаул: Изд-во АлтГТУ, 2008. – 168 с.

14. Ушаков И. А. Курс теории надежности систем: учеб. пособие для вузов / И.А. Ушаков. – М.: Дрофа, 2008. – 239 с.

15. Федотов А. В. Основы теории надежности и технической диагностики: конспект лекций / А. В. Федотов, Н. Г. Скабкин. – Омск: Изд-во ОмГТУ, 2010. – 64 с.

16. Феллер В. Введение в теорию вероятностей и ее приложения. Т.1, 2. – М.: Мир, 1984. – 528 с.

17. Шишмарев В. Ю. Надежность технических систем: учебник для студ. высш. учеб. заведений / В. Ю. Шишмарев. – М.: Издательский центр «Академия», 2010. – 304 с.

18. Яхьяев Н. Я. Основы теории надежности и диагностика: учебник для студ. высш. учеб. заведений / Н. Я. Яхьяев, А. В. Кораблин. – М.: Издательский центр «Академии», 2009. – 256 с.

19. ГОСТ 27.204-83 Надежность в технике. Технологические системы. Требования к оценки по параметрам производительности.

20. ГОСТ 27.002-89. Надежность в технике. Основные понятия. Термины и определения.

21. ГОСТ 4.413-86: СПКП. Котлы теплофикационные водогрейные. Номенклатура показателей.