лекция - математические основы надежности. Лекция 3 матема

• Название: Лекция 3 матема
• Дата: 01.12.2022
• Размер: 315.5 Kb.
• Имя файла: лекция - математические основы надежности.docx
• Тип: Лекция; #823497
• страница: 1 из 3

Лекция 3
МАТЕМАТИЧЕСКИЕ ОСНОВЫ НАДЕЖНОСТИ
Математический аппарат для обработки случайных величин
Надежность объектов нарушается возникающими отказами. Отказы рассматривают как случайные события. Для количественной оценки надежности используются методы теории вероятности и матема-тической статистики.

Показатели надежности могут определяться:

– аналитическим путем на основе математической модели – мате-матического определения надежности;

– в результате обработки опытных данных – статистическое опре-деление показателя надежности.

Момент возникновения отказа, частота возникновения отказов – величины случайные. Поэтому базовыми методами для теории на-дежности являются методы теории вероятности и математической статистики.

Случайная величина – величина, которая в результате опыта при-нимает одно, наперед неизвестное значение, зависящее от случайных причин. Случайные величины могут быть дискретными и непрерыв-ными.

Как известно из теории вероятности и математической статистики, общими характеристиками случайных величин являются:

1. Среднее арифметическое значение.
Х=ƩХi/n

где x_i – реализация случайной величины в каждом наблюдении; n – число наблюдений.

2. Размах. Понятие размаха в теории статистики используется в качестве меры рассеивания случайной величины.

R = x_max – x_min ,

где x_max – максимальное значение случайной величины; x_min – минимальное значение случайной величины.

3. Среднее квадратическое отклонение является также мерой рассеивания случайной величины.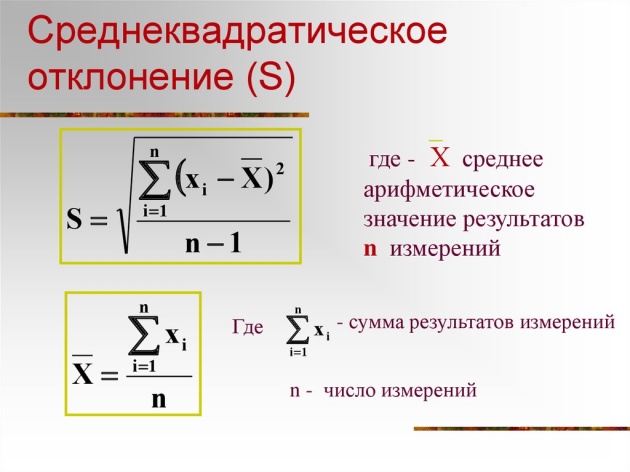


4. Коэффициент вариации также характеризует рассеивание случайной величины с учетом средней величины. Коэффициент вариации определяется по формуле
V =S/X.

Различают случайные величины с малой вариацией (V≤0,1), средней вариацией (0,1<V≤0,33) и большой вариацией (V>0,33). Если коэффициент вариации V<0,33, то случайная величина подчиняется нормальному закону распределения. Если коэффициент вариации 0,33<V≤1, то – распределению Вейбулла. Если коэффициент вариации V=1, то – равновероятному распределению.

В теории и практике надежности чаще всего используются следующие законы распределения: нормальный, логарифмически нормальный, Вейбулла, экспоненциальный.

Законом распределения случайной величины называется соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Для характеристики закона распределения случайной величины используются следующие функции.

1. Функция распределения случайной величины – функция F(х), оп-ределяющая вероятность того, что случайная величина Х в результате испытаний примет значение меньше или равное х:

F(x) = P(X ≤ x).

Функция распределения случайной величины может быть пред-ставлена графиком (рис. 1).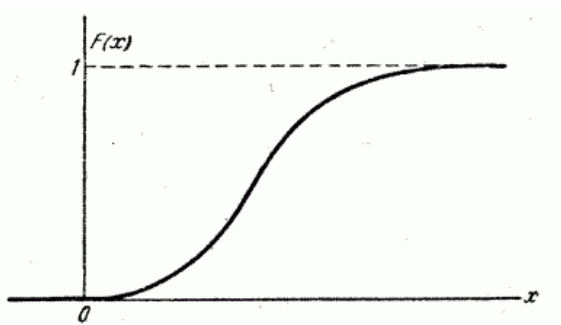

Рис. 1. Функция распределения случайной величины

2. Плотность распределения вероятностей случайной величины

f (x) = F'(x).
Плотность вероятности характеризует вероятность того, что слу-чайная величина примет конкретное значение x (рис. 2).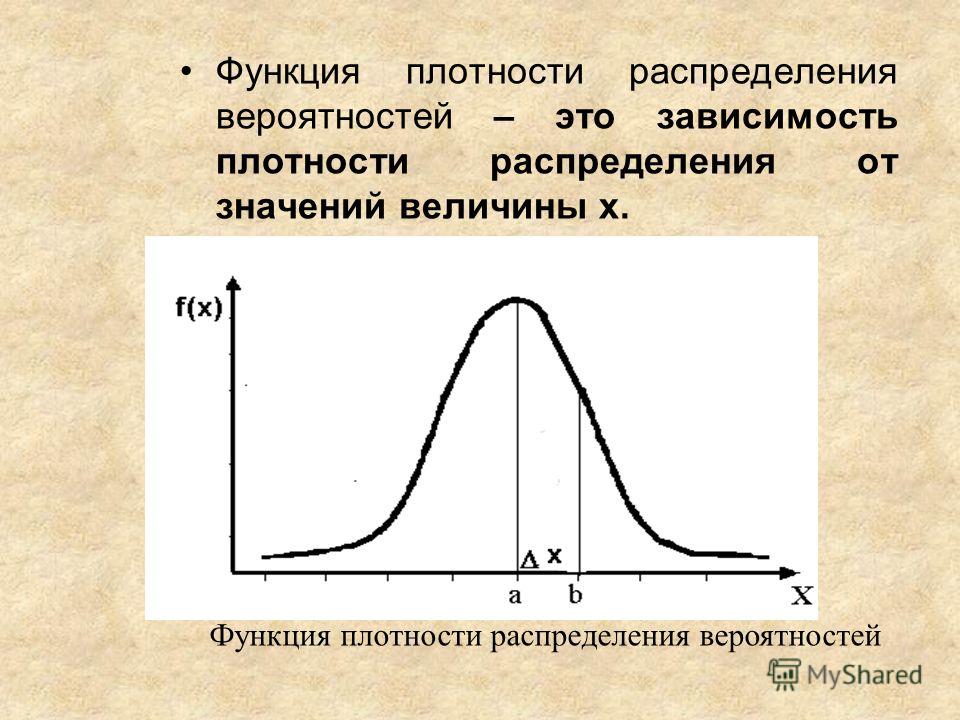


Рис. 2. Плотность распределения вероятностей (нормальный закон распределения)

Экспериментальной оценкой плотности вероятности случайной величины является гистограмма распределения случайной величины (рис.3).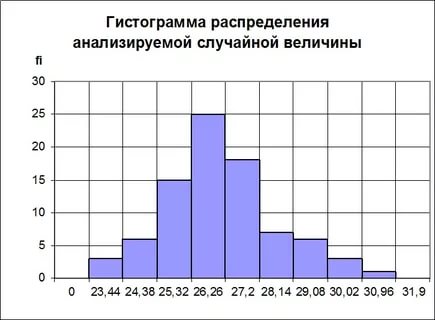


Рис. 3. Гистограмма распределения случайной величины

Гистограмма показывает зависимость количества наблюдаемых значений случайной величины в определенном интервале значений от границ этих интервалов. По гистограмме можно приближенно судить о плотности распределения случайной величины.

При построении гистограммы в выборке случайной величины x из n значений определяют наибольшее x_max и наименьшее x_min значения. Диапазон изменения величины R разбивают на m одинаковых интервалов. Затем подсчитывают число наблюдаемых значений случайной величины n_i, попадающих в каждый i-й интервал.