Методы распознавания образов: эвристические методы. Реферат ТОИ Эвристические методы. Методы распознавания образов
 Скачать 0.62 Mb. Скачать 0.62 Mb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственое автономное образовательное учреждение высшего профессионального образования «Северо-Восточный федеральный университет имени М.К.Аммосова» Институт математики и информатики РЕФЕРАТ на тему МЕТОДЫ РАСПОЗНАВАНИЯ ОБРАЗОВ: ЭВРИСТИЧЕСКИЕ МЕТОДЫ Выполнила: Птицына Нюргуяна Алексеевна Студентка 4 курса, группы ПОИМ-18 Проверила: Николаева Наталья Васильевна к.ф.-м.н, зав.кафедрой ИТ ИМИ Якутск – 2021 ОГЛАВЛЕНИЕВведение 4 1.Предмет распознавания образов 5 2. Эвристические методы распознавания образов 6 Эвристика – в широком смысле раздел психологии, раскрывающий природу мыслительных операций человека при решении различных задач независимо от их конкретного содержания. В более узком смысле – эвристика – это догадки, основанные на общем опыте решения родственных задач. Попытки систематизировать эвристику принадлежат Р. Декарту, Г. Лейбницу, Б. Больцано и др. В большинстве случаев эвристика – прием, позволяющий сокращать количество просматриваемых вариантов при поиске решения задачи, причем этот прием обычно не гарантирует наилучшее решение. Например, человек, играя в шахматы, пользуется эвристическими приемами выработки решений, т.к. продумать весь ход игры с начала до конца практически невозможно из-за слишком большого количества вариантов игры. Методы эвристики широко применяются в кибернетике [1, с. 364]. 6 Эвристические методы в распознавании — методы решения задач распознавания, обучения или самообучения распознаванию, основанные на интуитивных, опирающихся на предшествующий опыт, соображениях. Этим эвристические методы в распознавании отличаются от формальных методов, логически выводимых из определенных гипотез о множествах распознаваемых сигналов, о классе, к которому заведомо принадлежит решающая функция, и т. п. Эвристические методы могут привести к быстрому и успешному решению той или иной проблемы в тех случаях, когда имеется опыт решения сходных в каком-либо отношении проблем. В подобных случаях решение удается найти без больших затрат усилий и времени на изучение закономерностей, специфичных для данной конкретной проблемы. Решение находят на основе аналогий и не вполне осознанных ассоциаций с решениями других похожих проблем. 6 Целенаправленная деятельность человека в подавляющем большинстве случаев является эвристической, т. к. формальные правила для наилучших в каком-либо смысле действий почти всегда неизвестны. В качестве типичного примера можно привести игру в шахматы, для которой стратегия, приводящая к выигрышу, неизвестна. Тем не менее, человек, используя накопленный опыт и различные интуитивные соображения, может играть в шахматы настолько успешно, что вычислительная машина, обладающая колоссальными преимуществами в скорости просмотра вариантов продолжения игры, не может соперничать с сильным шахматистом. Наиболее яркий пример эвристических методов в распознавании представляет собой персептрон. Американский нейрофизиолог Ф. Розенблатт предложил принцип действия персептрона по аналогии с известными из физиологии схемами связей между нервными клетками в живом мозге. Ф. Розенблатт пришел к весьма эффективному методу обучения распознающей системы. С формальной точки зрения этот метод представляет собой сходящийся итерационный алгоритм отыскания гиперплоскости, разделяющей два точечных множества в одномерном пространстве признаков. Персептрон можно с успехом использовать для решения задач обучения в тех случаях, когда в выбранном пространстве признаков такая разделяющая гиперплоскость существует [1, с. 365]. 7 3. Недостатки эвристических методов распознавания объектов и эффективность 8 4. Некоторые эвристические методы распознавания 8 Заключение 12 Список литературы 13 1.Ивахненко А. Г. Системы эвристической самоорганизации в технической кибернетике. К., 1971 [с. 364—367]; 13 2.Кудрявцев В.Б. Интеллектуальные системы, 2018. 13 3.Лепский А.Е., Броневич А.Г. Математические методы распознавания образов: Курс лекций. – Таганрог: ТТИ ЮФУ, 2009. – 155 с. 13 4.Черногорова Ю.В. Методы распознавания образов / Молодой учёный. Международный научный журнал №28. – 1 Ч. – Казань: Молодой ученый, 2016. – 102 с. 13 ВведениеВ последние годы распознавание образов находит все большее применение в повседневной жизни. Распознавание речи и рукописного текста значительно упрощает взаимодействие человека с компьютером, распознавание печатного текста используется для перевода документов в электронную форму. Популярно мнение, что распознавание, как и прочие алгоритмы искусственного интеллекта, есть черная магия, недоступная простым смертным. На самом же деле алгоритмы, лежащие в основе распознавания, довольно очевидны, нужно лишь зайти чуть издалека и определиться с терминами. Задачи распознавания образов связаны с классификацией объектов, которая подчинена некоторой цели. Распознавание образов - относительно новая область математической кибернетики, но она интенсивно развивается, и уже сейчас имеются многочисленные важные приложения методов распознавания буквально во всех сферах науки и техники, в том числе в экономике, технике, медицине, физике, биологии, социологии и так далее. Распознавание образов является основой искусственного интеллекта. Одним из методов распознавания образов является эвристический метод. Предмет распознавания образов Распознавание образов – это наука о методах и алгоритмах классификации объектов различной природы. С задачей распознавания любой человек сталкивается ежеминутно. Например, мы узнаем людей и предметы, распознаем буквы и цифры, понимаем речь, распознаем с разной степенью успешности опасные ситуации. Можно сказать, что живые организмы вынуждены в процессе своей жизнедеятельности постоянно решать задачи распознавания. От успешности решения этих задач зависит успешность функционирования и даже жизнь биологического организма. Любая здоровая биологическая особь обладает чрезвычайно развитыми способностями к распознаванию образов. Решение задач распознавания – это необходимый атрибут взаимодействия живого организма с внешней средой. В последние десятилетия различные задачи распознавания все чаще решают с помощью средств вычислительной техники. Более того, с развитием средств вычислительной техники появились возможности для решения тех задач распознавания, которые ранее не могли быть решены. Можно выделить следующие наиболее важные направления развития интеллектуальных систем (т.е. систем, решающих задачи, традиционно относимые к интеллектуальной сфере), в которых широко используются методы распознавания образов: • распознавание символов (печатного и рукописного текстов, банковских чеков и денежных купюр и т.д.); • распознавание изображений, полученных в различных частотных диапазонах (оптическом, инфракрасном, радиочастотном, звуковом) и анализ сцен; • распознавание речи; • медицинская диагностика; • системы безопасности; • классификация, кластеризация и поиск в базах данных и знаний (в том числе и в Интернет-ресурсах) [3, с. 10]. Несмотря на то, что некоторые из этих задач решаются человеком на подсознательном уровне с большой скоростью, до настоящего времени ещё не создано компьютерных программ, решающих их в столь же общем виде. В связи с этим, проблема распознавания образов получила повсеместное распространение, в том числе в области искусственного интеллекта и робототехники. В связи с этим, проблема распознавания образов получила повсеместное распространение, в том числе в области искусственного интеллекта и робототехники [4, с. 40]. 2. Эвристические методы распознавания образовЭвристика – в широком смысле раздел психологии, раскрывающий природу мыслительных операций человека при решении различных задач независимо от их конкретного содержания. В более узком смысле – эвристика – это догадки, основанные на общем опыте решения родственных задач. Попытки систематизировать эвристику принадлежат Р. Декарту, Г. Лейбницу, Б. Больцано и др. В большинстве случаев эвристика – прием, позволяющий сокращать количество просматриваемых вариантов при поиске решения задачи, причем этот прием обычно не гарантирует наилучшее решение. Например, человек, играя в шахматы, пользуется эвристическими приемами выработки решений, т.к. продумать весь ход игры с начала до конца практически невозможно из-за слишком большого количества вариантов игры. Методы эвристики широко применяются в кибернетике [1, с. 364]. Эвристические методы в распознавании — методы решения задач распознавания, обучения или самообучения распознаванию, основанные на интуитивных, опирающихся на предшествующий опыт, соображениях. Этим эвристические методы в распознавании отличаются от формальных методов, логически выводимых из определенных гипотез о множествах распознаваемых сигналов, о классе, к которому заведомо принадлежит решающая функция, и т. п. Эвристические методы могут привести к быстрому и успешному решению той или иной проблемы в тех случаях, когда имеется опыт решения сходных в каком-либо отношении проблем. В подобных случаях решение удается найти без больших затрат усилий и времени на изучение закономерностей, специфичных для данной конкретной проблемы. Решение находят на основе аналогий и не вполне осознанных ассоциаций с решениями других похожих проблем. Целенаправленная деятельность человека в подавляющем большинстве случаев является эвристической, т. к. формальные правила для наилучших в каком-либо смысле действий почти всегда неизвестны. В качестве типичного примера можно привести игру в шахматы, для которой стратегия, приводящая к выигрышу, неизвестна. Тем не менее, человек, используя накопленный опыт и различные интуитивные соображения, может играть в шахматы настолько успешно, что вычислительная машина, обладающая колоссальными преимуществами в скорости просмотра вариантов продолжения игры, не может соперничать с сильным шахматистом. Наиболее яркий пример эвристических методов в распознавании представляет собой персептрон. Американский нейрофизиолог Ф. Розенблатт предложил принцип действия персептрона по аналогии с известными из физиологии схемами связей между нервными клетками в живом мозге. Ф. Розенблатт пришел к весьма эффективному методу обучения распознающей системы. С формальной точки зрения этот метод представляет собой сходящийся итерационный алгоритм отыскания гиперплоскости, разделяющей два точечных множества в одномерном пространстве признаков. Персептрон можно с успехом использовать для решения задач обучения в тех случаях, когда в выбранном пространстве признаков такая разделяющая гиперплоскость существует [1, с. 365]. 3. Недостатки эвристических методов распознавания объектов и эффективностьОсновным недостатком эвристических методов в распознавании является отсутствие гарантии успешного решения задачи. В случае неудачной попытки применить интуитивные соображения, пути продвижения к решению поставленной задачи остаются неопределенными. В подобных случаях приходится прибегать к детальному экспериментальному и теоретическому изучению закономерностей, специфичных для данной проблемы. В результате такого изучения могут либо возникнуть новые эвристические соображения, либо будет найдено достаточное количество данных для формальной постановки задачи и ее математические решения. Так, например, попытка применения простейшего «трехслойного» персептрона к распознаванию изображений в том случае, когда изображения, отличающиеся только переносом в поле зрения, надо отнести к одному классу, оказалась неудачной. Изучение проблемы показало, что для ее успешного решения необходимо ввести дополнительное ограничение: веса ассоциативных элементов, отличающихся переносом, должны быть одинаковыми. Часто эффективными являются комбинированные методы, основанные на одновременном использовании двух критериев выбора решений: формального и эвристического. Например, в случае, когда экспериментальных данных мало, а уравнение математической модели содержит много коэффициентов, только доопределение решения задачи по второму, эвристическому критерию позволяет найти единственную оптимальную оценку всех коэффициентов. При одном критерии задача не имеет единственного (регулярного) решения [1, с. 365]. 4. Некоторые эвристические методы распознавания Метод эталонов. Метод применим в случае, когда точки каждого класса расположены рядом друг с другом, а центры сгущения этих точек отстоят друг от друга на сравнительно большом расстоянии. Для каждого класса по обучающей выборке строится эталон х° = (х?,х§,... ,т°), имеющий значения признаков 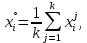 где { 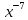 -7 = (xj, х?,..., -7 = (xj, х?,..., 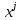 n) : j = 1,2,... А:} — множество объектов данного образа в обучающей выборке. Эталон — это усредненный по обучающей выборке абстрактный объект, он может не совпадать ни с одним объектом генеральной совокупности. n) : j = 1,2,... А:} — множество объектов данного образа в обучающей выборке. Эталон — это усредненный по обучающей выборке абстрактный объект, он может не совпадать ни с одним объектом генеральной совокупности.Принадлежность объекта х к тому или иному образу определяется по расстоянию до эталонов всех образов, и система относит х к тому образу, расстояние до эталона которого минимально. Расстояние измеряется в той метрике, которая введена для решения задачи распознавания. Как правило — это метрика Евклида, метрика "городских кварталов" или метрика Хэмминга. Метод дробящихся эталонов. Если метод эталонов работает не удовлетворительно, то его ошибки можно исправить с помощью дополнительных эталонов. Процесс обучения состоит в следующем. На первом этапе в обучающей выборке "охватывают" все объекты каждого класса гиперсферой возможно меньшего радиуса. Сделать это можно, например, так. Строится эталон каждого класса. Вычисляется расстояние от эталона до всех объектов данного класса, входящих в обучающую выборку. Выбирается максимальное из этих расстояний 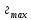 . Строится гиперсфера с центром в эталоне и радиусом R = . Строится гиперсфера с центром в эталоне и радиусом R = 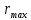 + е. Она охватывает все объекты данного класса. Такая процедура проводится для всех классов (образов). На рисунке 1.5 приведен пример двух образов в двухмерном признаковом пространстве. + е. Она охватывает все объекты данного класса. Такая процедура проводится для всех классов (образов). На рисунке 1.5 приведен пример двух образов в двухмерном признаковом пространстве.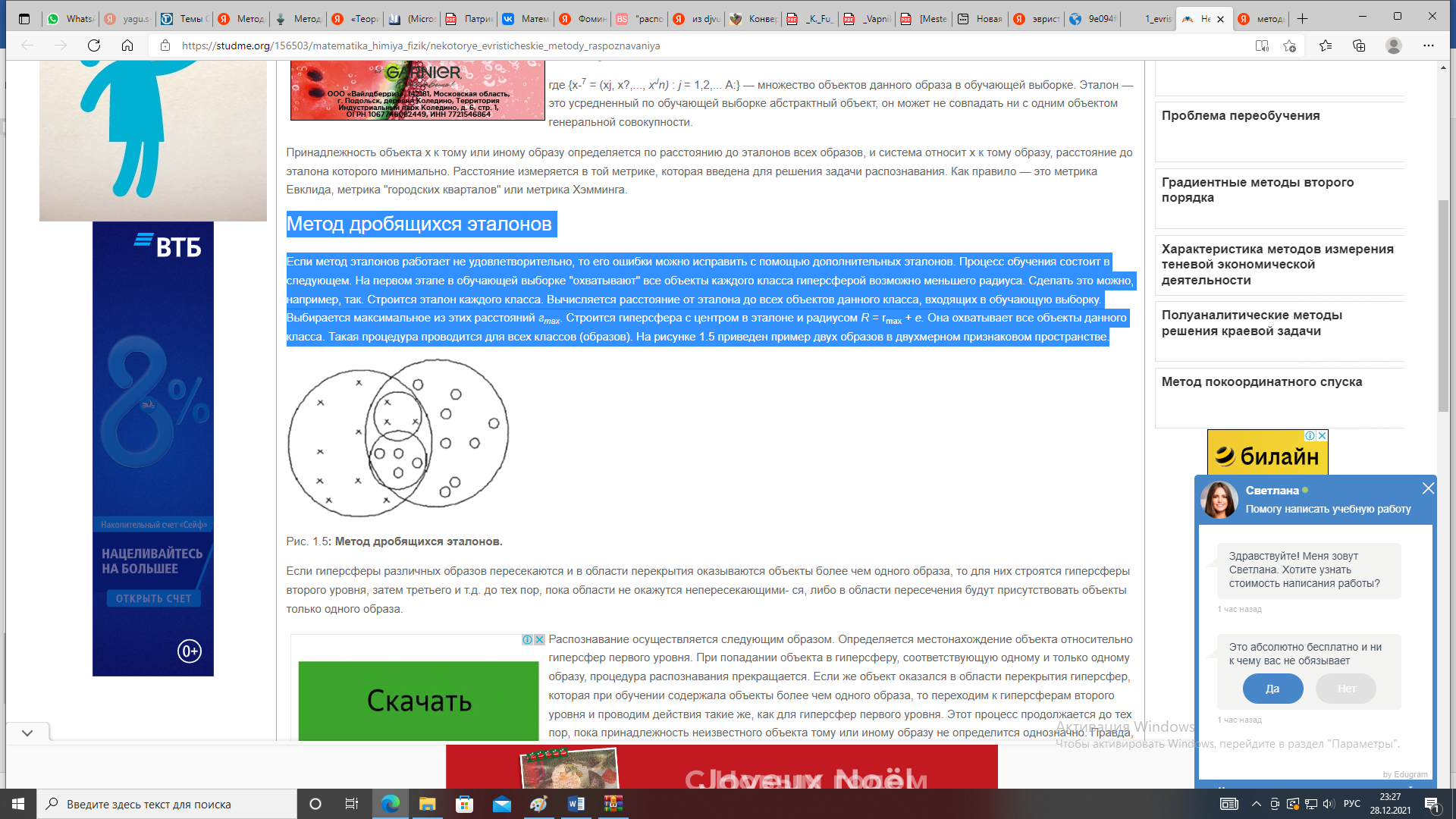 Если гиперсферы различных образов пересекаются и в области перекрытия оказываются объекты более чем одного образа, то для них строятся гиперсферы второго уровня, затем третьего и т.д. до тех пор, пока области не окажутся непересекающимися, либо в области пересечения будут присутствовать объекты только одного образа. Распознавание осуществляется следующим образом. Определяется местонахождение объекта относительно гиперсфер первого уровня. При попадании объекта в гиперсферу, соответствующую одному и только одному образу, процедура распознавания прекращается. Если же объект оказался в области перекрытия гиперсфер, которая при обучении содержала объекты более чем одного образа, то переходим к гиперсферам второго уровня и проводим действия такие же, как для гиперсфер первого уровня. Этот процесс продолжается до тех пор, пока принадлежность неизвестного объекта тому или иному образу не определится однозначно. Правда, это событие может и не наступить. В частности, неизвестный объект может не попасть ни в одну из гиперсфер какого-либо уровня. В этих случаях "учитель” должен включить в решающие правила соответствующие действия. Например, система может либо отказаться от решения об однозначном отнесении объекта к какому-либо образу, либо использовать критерий минимума расстояния до эталонов данного или предшествующего уровня и т.п. Какой из этих приемов эффективнее, сказать трудно, т.к. метод дробящихся эталонов носит в основном эмпирический характер [2]. Заключение Существует множество направлений по развитию данной науки. Распознавание - одно из ключевых направлений развития на данный момент. На сегодняшний день не существует единого метода или способа создания алгоритмов анализа изображения с выделением образов объектов. Так как машинное зрение находится в процессе развития и находит разнообразные ключи к пониманию данного пласта машинного обучения. Если посмотреть в прошлое, то мы заметим, как наука сделала огромный шаг к автоматизации человеческой деятельности. Поэтому в скором времени, возможно, произойдет научный прорыв и появятся новейшие методы и теории распознавания образов. А сейчас нужно трудиться и улучшать уже существующие для точной детализации и усовершенствования методов для определения объектов из динамичной сцены в реальном времени для обработки информации в компьютере робота. Список литературы Ивахненко А. Г. Системы эвристической самоорганизации в технической кибернетике. К., 1971 [с. 364—367]; Кудрявцев В.Б. Интеллектуальные системы, 2018. Лепский А.Е., Броневич А.Г. Математические методы распознавания образов: Курс лекций. – Таганрог: ТТИ ЮФУ, 2009. – 155 с. Черногорова Ю.В. Методы распознавания образов / Молодой учёный. Международный научный журнал №28. – 1 Ч. – Казань: Молодой ученый, 2016. – 102 с. |
