числовые методы. Методы решения нелинейных уравнений
 Скачать 1.33 Mb. Скачать 1.33 Mb.
|
|
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования «Московский технический университет связи и информатики» Кафедра «Информатика» Предмет: Вычислительные модели Лабораторная работа № 1 Тема: «Методы решения нелинейных уравнений»Вариант 11 Выполнил: Касимов А.М. Проверил: Преподаватель _________________ Москва 2023г. 1.2. Общее заданиеВыбрать индивидуальное задание из табл. 1-1:
нелинейное уравнение; методы решения нелинейного уравнения для выполнения 3-х итераций; Отделить корни заданного уравнения графическим и аналитическим методом с использованием средств математического пакета. Для каждого из заданных методов провести исследование функции нелинейного уравнения: проверить выполнение условий сходимости вычислительного процесса, в случае расходящегося процесса – сделать необходимые преобразования для обеспечения сходимости; выбрать начальное приближение к корню; сформулировать условие окончания этапа уточнения корня. С использованием итерационной формуле 1-го заданного метода провести расчет трех итераций с использованием средств мат. пакета. Результаты расчета свести в табл. 1-2. Оценить погрешность результата после 3-х итераций. Для 2-го заданного метода выполнить решение уравнения с точностью 10-4, создав программу, реализующую заданный метод. Произвести расчет, а результаты решений свести в табл. 1-2. 2 Отделение корней.
1-метод половинного деления,4-хорд. Произведем отделение корней при помощи программы MathCad 14. 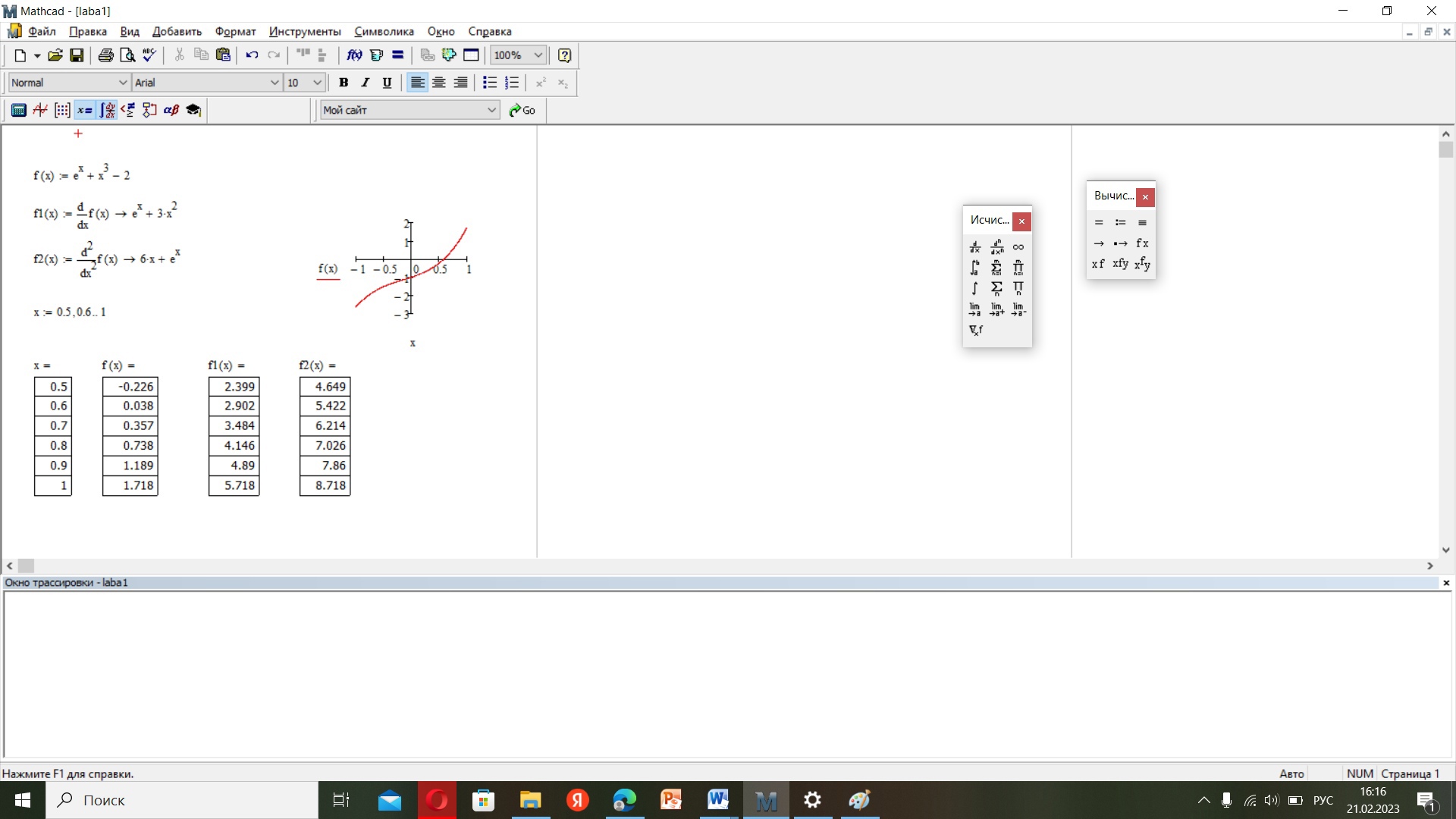 аaf аaf1-Произведем отделение корней при помощи программы MathCad 11. На интервале [0,5;1] функция имеет один корень, поэтому мы можем использовать этот интервал для расчётов и в этом случае f’(x) и f”(x) непрерывны и знакопостоянны и f(0,5)*f(1)<0 3 Ручной расчёт. Метод половинного деления 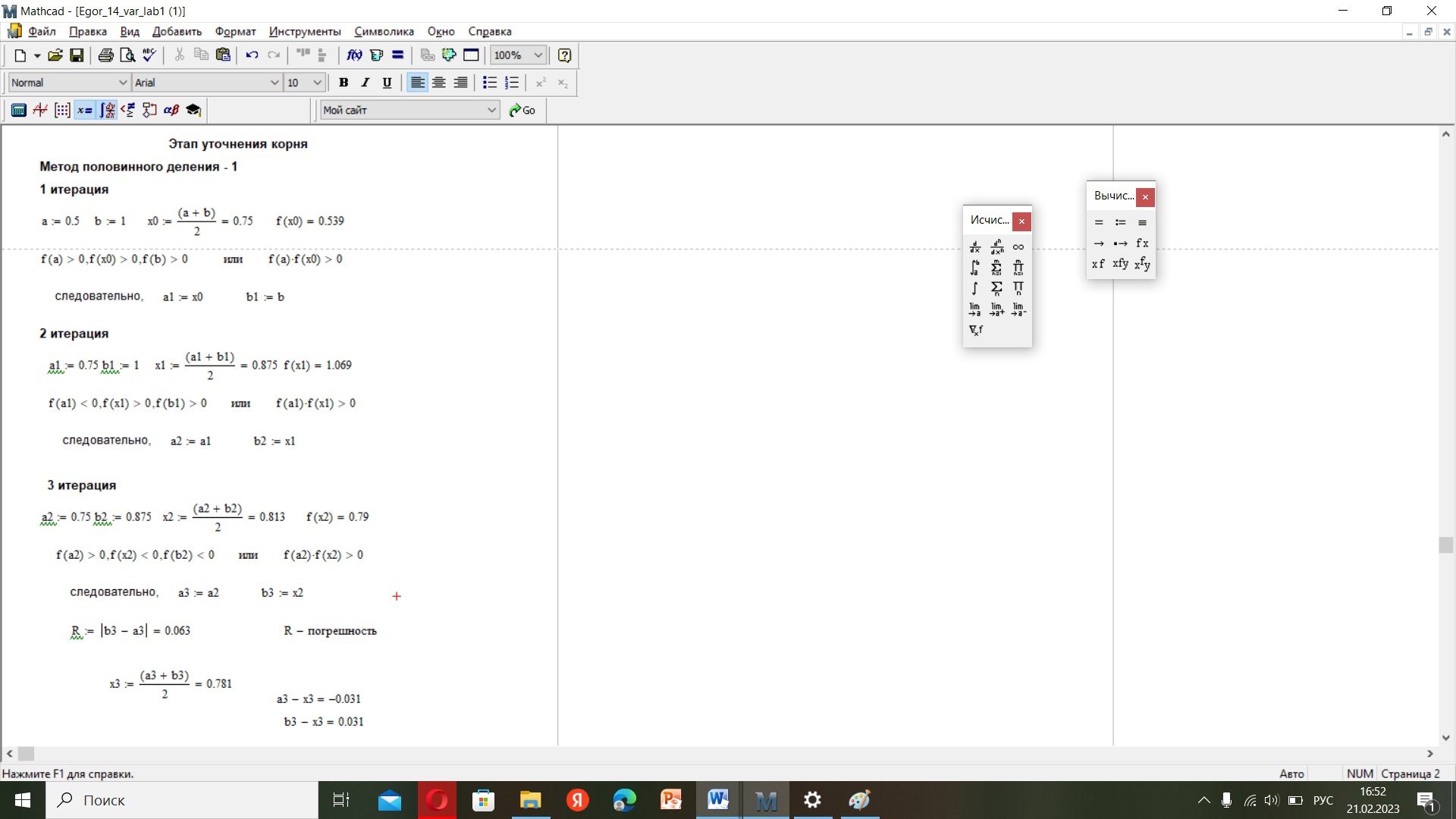 Результаты вычислений представлены в форме табл.
4.Расчет на ПК. 4.1.Программный код. #include #include using namespace std; double f(double x) { return sin(1 - 0.2 * (pow(x, 2))) - x; } double findRoot(double (*f)(double), double a = 0.5, double b = 1, double eps = 0.1) { double t; while (fabs(b - a) >= eps) { //1 t =( b*f(a)-f(b)*a)/(f(a)-f(b)); t = a + (f(b) * (b - a)) / (f(b) - f(a)); //2 if (f(a) * f(t) < 0) { b = t; //p cout << "b=" << b; } else if (f(t) * f(b) < 0) { a = t; //p cout << "a=" << a; } else return t; } return t; } int main() { double t = findRoot(f); cout << "x=" << t << " f(x)=" << f(t) << endl; return 0; } 4.3 Схемы алгоритма для процедур программы 1)схема процедура-функция: для вычисления значений нашей функции 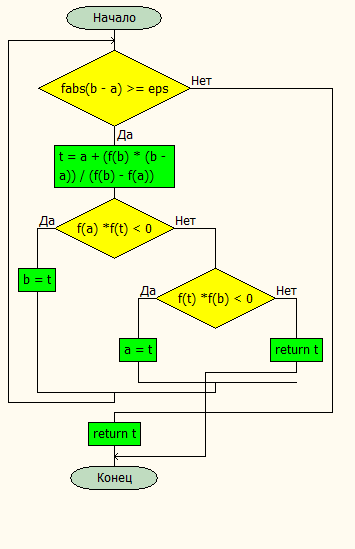 2-Схема-процедура для проверки сходимости и вычисления значений ф-ции 2)Main блок для вывода значений 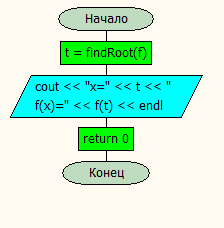 3-вывод на экран результатов 3)Результат программы 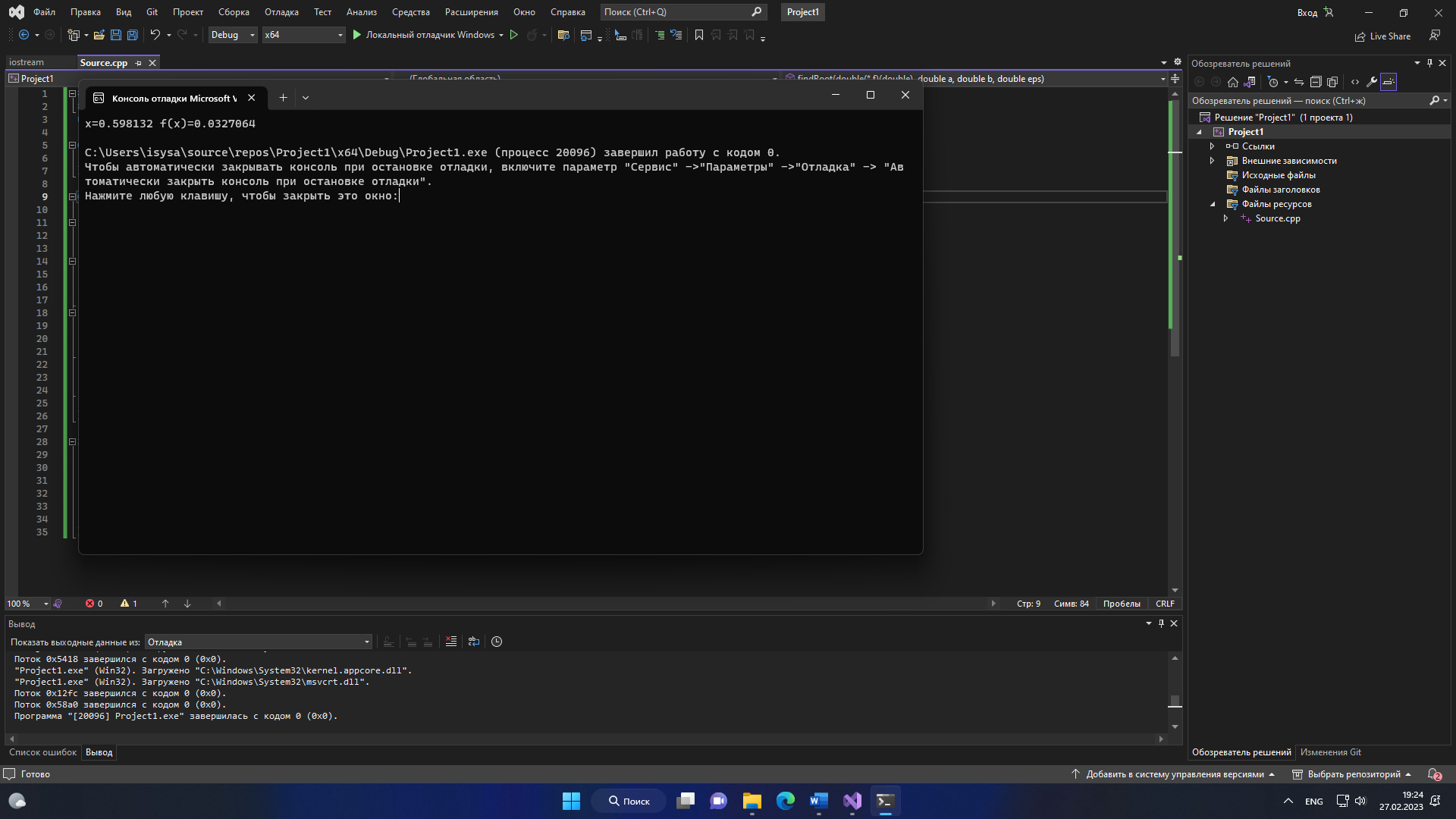 4-Результат программы 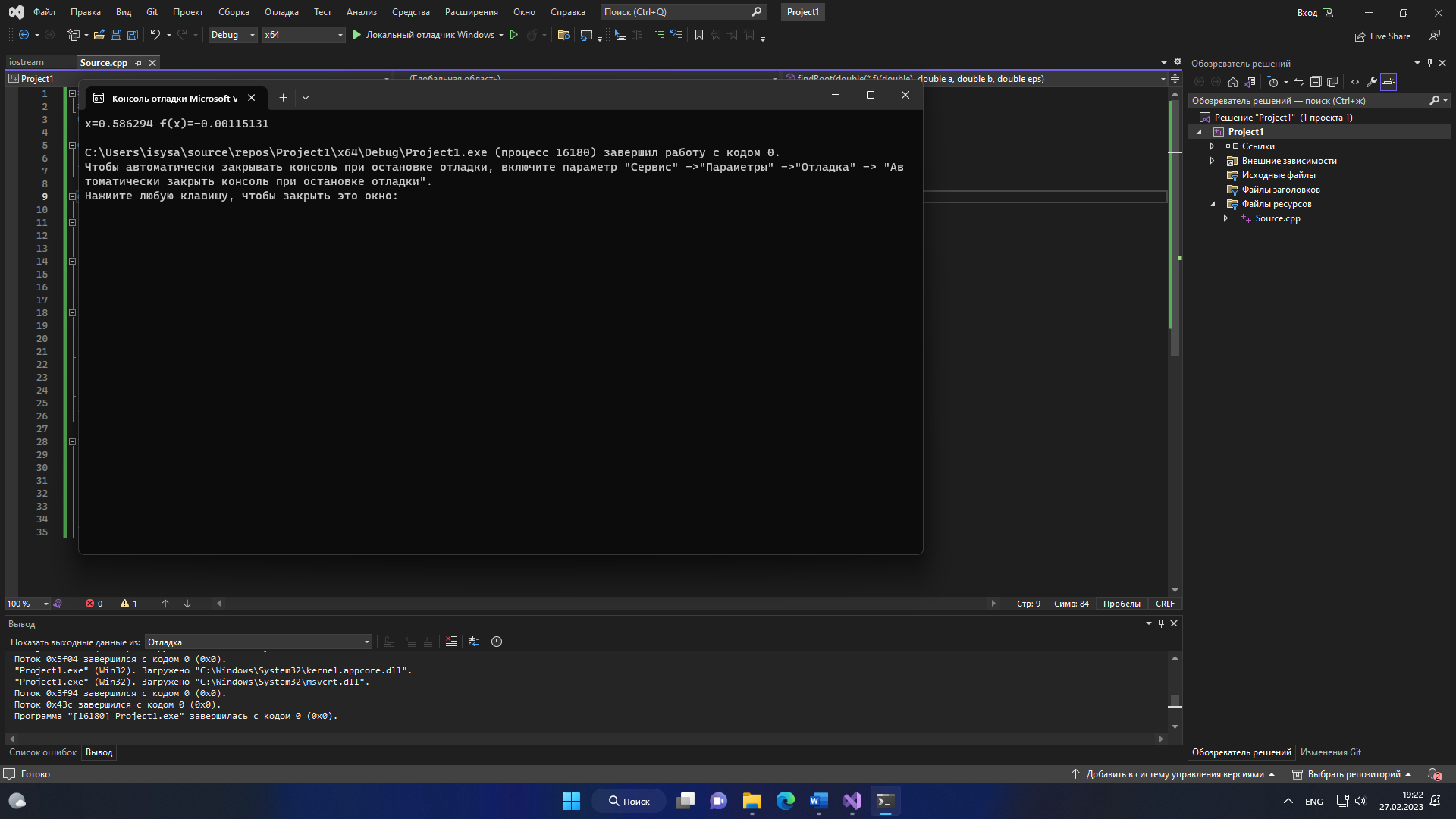 5-Результат программы 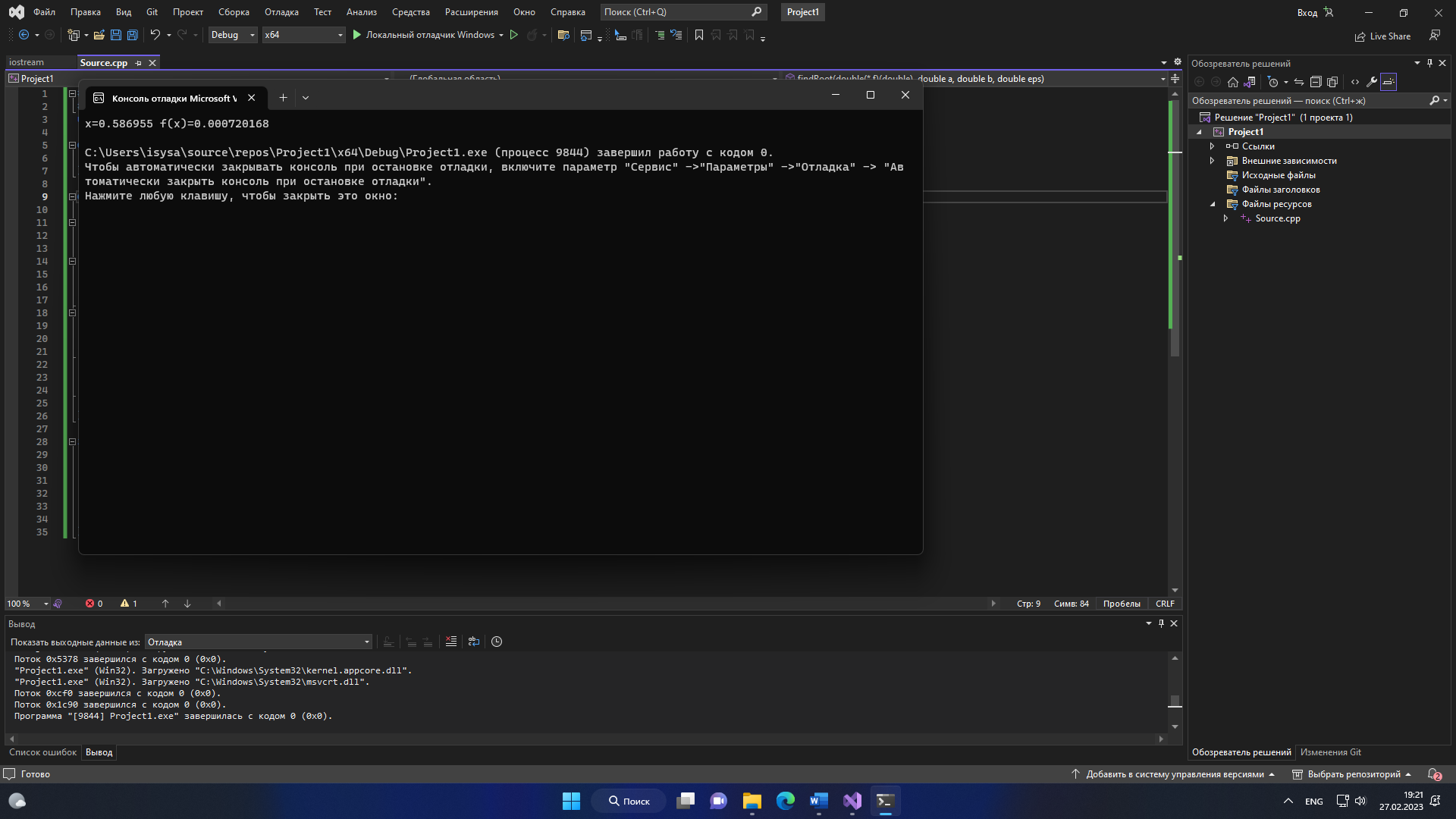 6-Результат программы 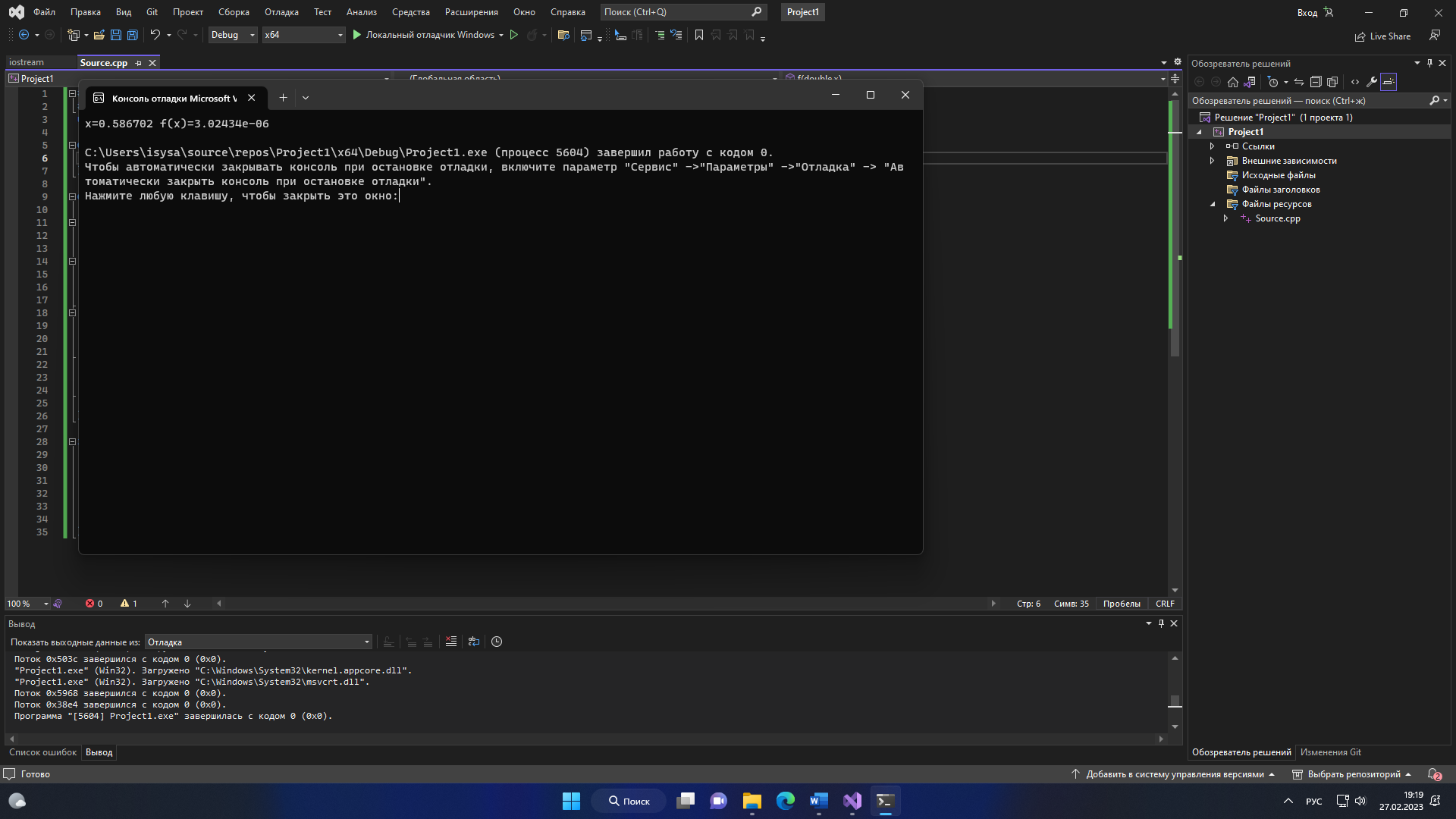 7-Результат программы 0.1-x=0.598132 f(x)= 0.0327064 0.01-x=0.586294 f(x)= -0.00115131 0.001-x=0.586955 f(x)= 0.000720168 0.0001-x=0.586702 f(x)= 3.02434e-06
8-Результаты решений |
