Курсовой. Методы уменьшения систематических погрешностей
 Скачать 73.17 Kb. Скачать 73.17 Kb.
|
 Министерство образования и науки Российской Федерации Филиал ФГБОУ ВО «Южно-Уральский государственный университет» (НИУ) в г. Миассе Машиностроительный факультет Кафедра «Техническая механика и естественные науки» Курсовая работа по дисциплине: «Физические основы измерений» на тему: «Методы уменьшения систематических погрешностей»
Миасс 2021 Содержание Оглавление Аннотация 2 Введение 3 Основная цель любого производства-это повышение качества продукции, которую они производят. В данной курсовой работе рассмотрим основные методы уменьшения систематических погрешностей, которые способствуют повышению качества: 3 Устранение источников погрешностей до начала измерений (профилактика погрешностей) 5 Исключение в измерения 7 поправок в 10 Заключение 13 Библиографический список 14
АннотацияЛуканин Егор Андреевич Курсовая работа Методы уменьшения систематических погрешностей Миасс: ЮУрГУ, 2021. Суть курсовой работы заключается в описании методов уменьшения систематических погрешностей. знания по « основы ». ВведениеОсновная цель любого производства-это повышение качества продукции, которую они производят. В данной курсовой работе рассмотрим основные методы уменьшения систематических погрешностей, которые способствуют повышению качества:Устранение источников погрешностей до начала измерений (профилактика погрешностей) Исключение погрешностей в процессе измерения. Внесение известных поправок в результат измерения. Таким образом целью данной курсовой работы является подробное рассмотрение методов уменьшения систематических погрешностей с примерами. Устранение источников погрешностей до начала измерений (профилактика погрешностей)Способ устранения предполагаемых погрешностей до начала измерений является наиболее рациональным, так как полностью или частично освобождает от необходимости устранять погрешности в процессе измерения или вычислять результат с учетом поправок. Перед измерением объект измерения должен быть изучен для корректного выбора его модели и средств измерений, проанализированы возможные источники систематических погрешностей для снижения влияния дополнительных погрешностей на результат измерения, приняты возможные меры для устранения влияния источников погрешностей. Под устранением источника погрешности понимается защита измерительной аппаратуры и объекта измерения от влияния источника погрешности либо удаление этого источника. Удалить источники значительных инструментальных погрешностей возможно при ремонте и регулировке, необходимость проведения которых выявляется при очередных и внеочередных поверках средств измерений. Систематические погрешности от неправильной установки могут быть значительно снижены при подготовке места установки средства измерения. Для температурной используются , т.е. стабильной (в ) температуры , кондиционирование и т.д. Для от влияния и полей из магнитомягких или с высокой . Для влияния полей средства . погрешностей от и вибраций приборов на , а также поглотителей - и пружинных , резины и т.п. погрешностей от и влажности можно, различных . принять для влияния на измеряемый , в которого изменения цепи при в нее измерения. Для различного . Исключение |
| | 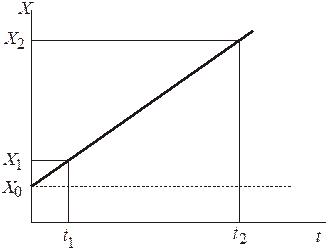 |
Идея способа состоит в том, что если переменная систематическая погрешность присутствует в результатах наблюдений, то s2 будет завышена. В то же время систематическая погрешность существенно меньше скажется на значениях последовательной разности (xi+1 –xi).
Рассчитав отношение дисперсий результатов наблюдений

и сравнив полученный результат с критерием Аббе , можно сделать вывод о том, присутствует периодическая систематическая погрешность в результатах или нет. Если рассчитанное значение n меньше критерия Аббе nq, при заданном уровне значимостиqи числе наблюденийn(n < nq), то можно сделать вывод о том, что периодическая систематическая погрешность присутствует.
Если выяснится, что имеется возрастающая или убывающая погрешность, то она должна быть количественно оценена и учтена в результатах наблюдений.
Часто применяются поправочные множители, на которые умножаются результаты измерения. Высокая точность исправленного результата измерения может быть получена лишь при условии, что поправка мала по сравнению с измеренным значением или поправочный множитель близок к единице.
Заключение
Исключение погрешностей устранением источников погрешностей, а также внесением поправок в результат измерения дает хорошие результаты, но, к сожалению, невозможно в полной мере устранить все систематические погрешности. Часто даже для хорошо изученных средств измерений и условий проведения измерений не удается внести поправки в результат. Влияющие величины в процессе измерения могут изменяться, и систематические погрешности, являющиеся их следствием, сложно отследить. В данной курсовой работе рассмотрев основные методы уменьшения систематических погрешностей приходим к выводу что, полное исключение систематических погрешностей практически невозможно, какая-то часть погрешности остается неустраненной, поэтому следует определять границы доверительного интервала неисключенных остатков систематической погрешности.
Библиографический список
1) Студопедия ЛЕКЦИЯ 6. §5. Методы уменьшения погрешностей измерений
https://studopedia.su/5_192_lektsiya-.html
2) Студопедия Методы уменьшения систематических погрешностей https://studopedia.ru/1_126865_metodi-umensheniya-sistematicheskih-pogreshnostey.html
3) Сергеев А.Г., Крохин В.В. Метрология: Учеб. пособие для вузов / Сергеев А.Г., Крохин В.В. - М.: Логос, 2001. - 408 с.: ил.
4) Аристов А.И. Метрология, стандартизация, сертификация / Аристов А.И. - М.: Академия, 2008. - 384с.
5) Радкевич Я.М. Метрология, стандартизация, сертификация / Радкевич Я.М. - М.: Высшая школа, 2010 - 792 с.
6) Димов Ю.В. Метрология, стандартизация и сертификация / Димов Ю.В. - СпБ.: Питер, 2010- 464с

 в измерения
в измерения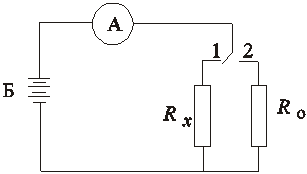
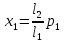
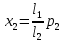
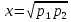

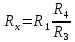




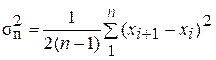 .
.