3799а Математические модели в управлении. Методы возможных направлений

Название	Методы возможных направлений
Дата	04.02.2023
Размер	412.5 Kb.
Формат файла
Имя файла	3799а Математические модели в управлении.doc
Тип	Документы #919831

Методы возможных направлений

Введение 2

1. Метод Зойтендейка 3

2. Построение возможных направлений спуска 6

3. Алгоритм метода Зойтендейка в случае линейных ограничений 9

4. Алгоритм Зойтендейка в случае нелинейных ограничений-неравенств 13

5. Модификация метода возможных направлений 18

Заключение 22

Список использованных источников 23

Введение

Методы возможных направлений – наиболее исследованный класс методов выпуклого программирования (задачи выпуклого программирования – это такие задачи нелинейного программирования, в которых целевые функции и функции ограничений выпуклы).

Подробное описание данных методов было произведено в работах Зойтендейка¹.

Хотя сходимость к глобальному минимуму может быть доказана только в случаях задач выпуклого программирования, тем не менее методы возможных направлений сходятся к локальному минимуму и в применении к задачам нелинейного программирования вообще.

Цель данной работы - рассмотреть сущность методов возможных направлений.

1. Метод Зойтендейка

Типичным представителем класса методов возможных направлений является метод Зойтендейка. На каждой итерации метода находят возможное направление спуска, а затем проводят оптимизацию вдоль этого направления. Для изложения идеи метода введем ряд необходимых понятий²:

Рассмотрим задачу минимизаци  при условии, что , где – непустое множество.

Ненулевой вектор  называется возможным направлением в точке , если существует такое , что  для всех .

Вектор  называется возможным направлением спуска в точке , если существует такое , что  и  для всех .

Сначала рассмотрим случай, когда ограничения линейные и задача НП имеет вид:

минимизировать                              (1)

при условиях                               (2)

                                          (3)

где  – матрица порядка ;

– матрица порядка ;

— -мерный вектор;

— -мерный вектор.

Справедливо следующее утверждение.
Лемма 1. Рассмотрим задачу минимизаци (1) - (3). Пусть - допустимая точка и предположим, что , где , а .

Ненулевой вектор  является возможным направлением в точке  в том и только в том случае, если  и . Если, кроме того, , то  является возможным направлением спуска.

Проиллюстрируем геометрически множество возможных направлений спуска на следующем примере.

Пример 1. Минимизировать   при условиях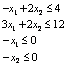

Выберем  и заметим, что первые два ограничения являются активными в этой точке. В частности, матрица  из вышеприведенной леммы 1, равна . Следовательно, вектор  является возможным направлением тогда и только тогда, когда  т.е. в том случае, если

На рис. 1. изображена совокупность этих направлений, образующая конус возможных направлений. Здесь 1 – конус возможных направлений; 2 – конус возможных направлений спуска; 3 – линии уровня целевой функции; 4 – полупространство направлений спуска.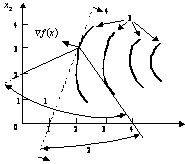

Рисунок 1
Если вектор удовлетворяет неравенству , то он является направлением спуска. Таким образом, совокупность возможных направлений спуска определяется открытым полупространством . Пересечение конуса возможных направлений с этим полупространством задает множество всех возможных направлений спуска.

2. Построение возможных направлений спуска

Пусть задана текущая допустимая точка x. Как показано в лемме 1, ненулевой вектор  будет возможным направлением спуска, если . Естественный подход к построению такого направления заключается в минимизации  при условиях: . Однако, если существует такой вектор , что , и выполняются условия а) и б), то оптимальное значение целевой функции сформулированной задачи равно – , так как ограничениям этой задачи удовлетворяет любой вектор , где  – любое большое число.

Следовательно, в задачу должно быть включено условие, которое бы ограничивало вектор . Такое ограничение называют нормирующим. Возможны различные формы нормирующего ограничения. Ниже приведем три задачи отыскания (наилучшего) направления спуска, в каждой из которых используются различные условия нормировки^³:

Задача :      минимизировать

при условиях

Задача : минимизировать

при условиях

Задача : минимизировать

при условиях

Задачи  и  являются задачами линейного программирования и, следовательно, их можно решить симплекс-методом.

Так как  является допустимой точкой в каждой из приведенных выше задач, а значение целевой функции в этой точке равно 0, то ее оптимальное значение в задачах , ,  не может быть положительным. Если минимальное значение ц.ф. в задачах , ,  отрицательно, то по лемме 6.1 нами построено возможное направление спуска. С другой стороны, если минимальное значение целевой функции равно нулю, то, как будет показано ниже, точка x является точкой Куна-Таккера.

Лемма 2. Рассмотрим задачу минимизаци  приусловиях . Пусть  – допустимая точка, в которой , где . Вектор является точкой Куна-Таккера тогда и только тогда, когда оптимальное значение целевой функции в задачах , ,  равно нулю.

Доказательство. Как следует из теоремы Куна-Таккера,  будет точкой Куна-Таккера тогда и только тогда, когда существуют векторы  такие, что

.                          (4)
Согласно следствию из леммы Фаркаша система (4) разрешима тогда и только тогда, когда система неравенств  не имеет решений, т.е. когда оптимальное значение целевой функции в задачах , ,  равно нулю.

Итак, мы показали, как найти возможное направление спуска.

Пусть теперь  – текущая точка;  – возможное направление спуска. В качестве следующей точки  выбирается , где длина шага  определяется из решения следующей задачи одномерной оптимизации:

минимизировать  по                 (5)

при условиях

,                                    (6)

.                                   (7)

Предположим, что . Тогда задачу (5) - (7) можно упростить следующим образом. Заметим, что . Значит, ограничение (7) излишне. Так как , то  для всех . Итак, остается только одно ограничение , и задача оптимизации (5) - (7) приводится к следующей задаче одномерной оптимизации:

минимизировать  по                 (8)

при условии

,

где 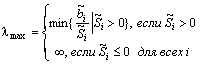                                            (9)

.                         (10)

3. Алгоритм метода Зойтендейка в случае линейных ограничений

Пусть требуется найти  при условиях .

Алгоритм метода состоит из предварительного и основного этапов. Последний в свою очередь состоит из однотипных итераций^⁴:

Предварительный этап. Найти начальную допустимую точку, для которой . Положить  и перейти к основному этапу.

Основной этап. -я итерация. Первый шаг. Пусть задан вектор . Предположим, что  и . В качестве возможного направления спуска  взять оптимальное решение следующей задачи:

минимизировать                              (11)

при условиях

                                       (12)

.                              (13)

Если , то остановиться, и – оптимальное решение (точка Куна-Таккера). В противном случае перейти ко второму шагу.

Второй шаг. Положить  равным оптимальному решению приведенной ниже задачи одномерной оптимизации:

минимизировать

при условии                          ,

где  задается формулой (9).

Для решения этой задачи можно применить любой метод одномерного поиска, например метод Фибоначчи.

Вычислить , определить новое множество активных ограничений для решения  и переопределить  и . Заменить  на  и перейти к первому шагу следующей итерации.

Рассмотрим задачу, в которой допустимая область задается системой ограничений-неравенств нелинейного типа:

минимизировать                            (14)

при условиях                                                   (15)

В следующей теореме формулируются достаточные условия, при которых вектор  является возможным направлением спуска.

Теорема 2. Рассмотрим задачу нелинейного программирования (14), (15). Пусть  – допустимая точка, а  – множество индексов активных в этой точке ограничений, т.е.. Предположим, кроме того, что функции  для  дифференцируемы в точке , а функции  для  непрерывны в этой точке. Если ,  при , то вектор  является возможным направлением спуска.

Доказательство. Пусть вектор  удовлетворяет неравенствам ,  при . Сначала укажем, что для  выполняются неравенства  и так как  непрерывны в точке , то  для достаточно малых . В силу дифференцируемости функции ,  имеем  , где  при . Так как , то  при достаточно малых . Следовательно, точка  допустима для малых значений . Аналогично из  следует, что для достаточно малых  .

Таким образом, вектор  является возможным направлением спуска.

На рис. 2 показана совокупность возможных направлений в точке . Здесь использованы такие обозначения: 1 – первое ограничение, 2 – третье ограничение, 3 – четвертое ограничение, 4 – второе ограничение, 5 – возможные направления спуска, 6 – линии уровня целевой функции. Вектор , удовлетворяющий равенству , является касательным к кривой линии (или поверхности) . Поскольку функции  нелинейны, то движение вдоль такого вектора может привести в недопустимую точку, что вынуждает требовать выполнения строгого неравенства .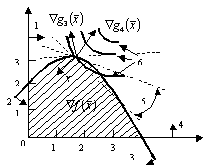

Рисунок 2
Чтобы найти вектор , удовлетворяющий неравенствам  ,   для  , вполне естественно минимизировать максимум из величин  и   для . Обозначим этот максимум через   . Вводя нормирующие условия , для всех , приходим к следующей вспомогательной задаче нахождения возможного направления спуска:

минимизировать                            (16)

при условиях

,                             (17)

,                      (18)

.                         (19)

Пусть  – оптимальное решение этой задачи ЛП. Если , то, очевидно,  – возможное направление спуска. Если же , то, как будет показано ниже, точка  является точкой Куна-Таккера.

Докажем это утверждение. Оптимальное значение целевой функции  в задаче (16) - (19) равно нулю тогда и только тогда, когда система неравенств ,  при  несовместна. Но, согласно следствию из леммы Фаркаша, для того чтобы эта система не имела решения, необходимо и достаточно, чтобы существовали такие числа , что

(20)

и либо , либо  для некоторого , а это одно из условий оптимальности теоремы Куна-Таккера.

4. Алгоритм Зойтендейка в случае нелинейных ограничений-неравенств

Далее рассмотрим алгоритм Зойтендейка при нелинейных ограничениях-неравненствах^⁵:

Предварительный этап. Выбрать точку , для которой . Положить  и перейти к основному этапу.

Основной этап. Первый шаг. Положить  и решить задачу:

минимизировать                            (20)

при условиях

,                             (21)

.          (22)

Пусть  – оптимальное решение задачи (20) – (22). Если , то конец алгоритма и точка  – оптимальное решение такой задачи одномерной оптимизации. Если , то перейти ко второму шагу.

Второй шаг.

минимизировать                  (23)

при условии ,                      (24)

где                              .     (25)

Положить , заменить  на  и перейти к первому шагу следующей итерации.

Пример 4. Рассмотрим задачу:

минимизировать

при условиях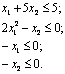



Будем решать эту задачу методом Зойтендейка, начиная поиск из точки . Заметим, что

Первая итерация. Первый шаг. В точке  имеем , а множество индексов активных ограничений есть . При этом . Задача нахождения возможного направления имеет вид

минимизировать

при условиях

Можно проверить, решая эту задачу симплекс-методом, что оптимальным решением этой задачи является вектор  и .

Второй шаг. Линейный поиск. Любая точка по направлению  из точки  может быть представлена в виде , а соответствующее ей значение целевой функции равно . Максимальное значение , для которого точка  остается допустимой, равно . Итак, решаем задачу одномерной минимизации:

минимизировать

при условии

Оптимальное значение . Итак, .

Вторая итерация. Первый шаг. В точке  имеем . Активных ограничений в этой точке нет, поэтому задача определения направления спуска имеет вид:

минимизировать z

при условиях

Оптимальным решением является вектор , а .

Второй шаг. Легко проверить, что , при котором точка  допустима, равна 0.3472. При этом активным становится ограничение . Оптимальное значение  находим в результате решения задачи:

минимизировать  z

при условии

Оно равно 0.3472, так что . Остальные итерации проводятся аналогично. Результаты вычислений на первых четырех итерациях метода приведены в табл. 1.

Таблица 1

			Поиск направления Линейный поиск

1	0.00;–0.75	-3.375	-5.50;–3.00	1.000;–1.000	-1.000	0.4140	0.2088	0.2083;–0.5417
2	0.208;–0.541	-3.635	-4.25;–4.25	1.000;–1.000	-8.5	0.3472	0.3472	0.555;–0.889
3	0.555;–0.889	-6.346	-3.556;–3.555	1.000;–0.533	-1.663	0.0924	0.0924	0.648;–0.840
4	0.648;–0.840	-6.468	-3.088;–3.937	-0.517; 1.000	-2.340	0.0343	0.0343	0.630;–0.874

На рис. 3 показан процесс поиска оптимума. Заметим, что следующей точкой будет , а значение целевой функции в этой точке равно –6.544, тогда как в оптимальной точке значение ц.ф. равно –6.559.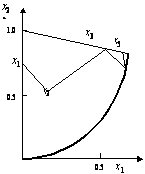

Рисунок 3
Метод возможных направлений может быть модифицирован на случай, когда кроме ограничений неравенств имеются нелинейные ограничения-равенства. Для иллюстрации обратимся к рис. 4, который отвечает единственному ограничению-равенству. Для заданной допустимой точки в этом случае не существует ненулевого направления такого, что при , для некоторого . Это затруднение можно преодолеть, если двигаться вдоль касательного направления , для которого , а затем скорректировать это движение и вернуться в допустимую область (рис. 4).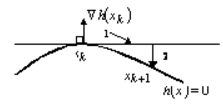

Рисунок 4
Поясним этот подход на примере:

минимизировать                   (26)

при условиях

,

.                        (27)

Пусть  – допустимая точка и . Будем решать следующую задачу ЛП:

минимизировать                      (28)

при условиях

,                           (29)

.                        (30)

Искомое направление  является касательным к ограничениям-равенствам и к некоторым активным нелинейным ограничениям-неравенствам. Линейный поиск вдоль  и последующее возвращение в допустимую область приводят в точку , после чего процесс поиска повторяется. Один из существенных недостатков рассмотренного варианта метода состоит в том, что если точка , которая задает текущее решение, окажется близка к границе, определяемой одним из ограничений, а оно не используется в процессе нахождения направления движения, то может оказаться, что сделав лишь небольшой шаг, мы окажемся на границе, определяемой этим ограничением. Поэтому оказывается целесообразным расширить множество активных ограничений , определив его так:

, где  – достаточно малое число^⁶.

5. Модификация метода возможных направлений

Анализ алгоритма Зойтендейка показал, что он может не сходиться к точке Куна-Таккера. Трудность здесь заключается в том, что длина шагов вдоль генерируемых направлений стремится к нулю, вызывая «заедание» процесса в неоптимальной точке. Во избежание этого Топкинс и Кейнотт разработали модификацию метода возможных направлений. Эта модификация гарантирует сходимость алгоритма к точке Куна-Таккера. Итак, рассмотрим задачу^⁷:

минимизировать

при условиях                 .

При заданной допустимой точке  возможное направление находят, решая следующую задачу ЛП:

минимизировать                            (31)

при условиях

,                                    (32)

,                         (33)

.                             (34)

Как видим, в этой модификации при определении направления движения учитываются все ограничения как активные, так и неактивные.

В отличие от метода возможных направлений, описанного выше, здесь мы не сталкиваемся с неожиданным изменением направления, когда приближаемся к границе множества допустимых решений, определяемой неактивным в текущей точке ограничением.

Дадим описание модифицированного алгоритма возможных направлений^⁸:

Начальный этап. Выбрать начальную точку , для которой  при . Положить  и перейти к основному этапу.

Основной этап. Первый шаг. Положить  равным оптимальному решению задачи ЛП:

минимизировать                            (35)

при условиях ,                      (36)

,                   (37)

.                             (38)

Если , то остановиться,  является точкой Куна-Таккера. В противном случае (при ) перейти ко второму шагу.

Второй шаг. Положить  равным оптимальному решению задачи:

минимизировать              (39)

при условии ,

где . (40)

Положить , заменить  на  и перейти к первому шагу.

Пример 5. Рассмотрим задачу:

минимизировать

при условиях

Применим для решения модифицированный алгоритм возможных направлений. Выберем в качестве начальной точки . Заметим, что в этой точке , а градиенты функций-ограничений соответственно равны .

Первая итерация. Первый шаг.

В точке  имеем . Задача поиска направления спуска имеет вид:

минимизировать

при условиях

В правой части ограничений этой задачи, кроме первого, стоят значения . Заметим, что одно из ограничений ( ) повторяется дважды, следовательно, одно из ограничений можно опустить. Оптимальным решением этой задачи является вектор , при котором .

Второй шаг (линейный поиск). Решаем задачу:

минимизировать

Максимальное значение , для которого точка  допустима, определяется соотношением (40) и равно . Тогда оптимальным решением задачи (41) будет .

Таким образом, .

Вторая итерация. Первый шаг. В точке  имеем . В качестве направления  берется оптимальное решение следующей задачи:

минимизировать

при условиях

Оптимальным решением этой задачи является вектор .

Второй шаг. Максимальное значение , для которого точка  допустима, равно . Легко можно проверить, что  достигает минимума на отрезке  в точке . Следовательно, . Далее этот процесс повторяется. В табл. 2 приведены результаты вычислений на первых пяти итерациях.

Таблица 2

			Первый шаг Второй шаг

1	0.00;–0.75	-3.375	-5.50;–3.00	0.714;-0.0357	-0.714	0.84	0.84	0.600;–0.720
2	0.600;–0.720	-5.827	-3.04; -4.32	-0.0712; –0.117	-0.288	1.562	1.562	0.489;–0.902
3	0.489;–0.902	-6.145	-3.849;–3.369	0.0957;–0.0555	-0.1816	1.564	1.564	0.6385;–0.8154
4	0.6385;–0.8154	-6.343	-5.63 ;–4.02	-0.016;–0.0433	-0.0840	1419	1.419	0.616;– 0.877
5	0.616;–0.877	-6.508	-3.29;–3.725	0.0268;–0.0132	-0.0303	1.455	1.455	0.655;–0.858

Траектория движения точки, задающей текущее решение, показана на рис. 5. В конце пятой итерации получена точка со значением целевой функции –6.559. Заметим, что в оптимальной точке значение целевой функции равно –6.613.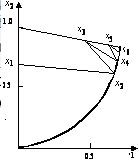

Рисунок 5

Заключение

Методы возможных направлений – наиболее исследованный класс методов выпуклого программирования (задачи выпуклого программирования – это такие задачи нелинейного программирования, в которых целевые функции и функции ограничений выпуклы).

Идея метода возможных направлений заключается в том, что в каждой очередной точке находится направление спуска такое, что перемещение точки по этому направлению на некоторое расстояние не приводит к нарушению ограничений задачи. Таким образом, метод возможных направлений можно рассматривать как естественное распространение метода градиентного спуска на задачи минимизации с ограничениями.

В отличие от других численных методов решения таких задач, метод возможных направлений обладает тем преимуществом, что для отыскания направления спуска достаточно решить задачу линейного программирования с небольшим числом ограничений.

Список использованных источников

Аттетков А.В., Галкин С.В., Зарубин В.С. Методы оптимизации: Учеб. для вузов / Под ред. B.C. Зарубина, А. П. Крищенко. - М.: МГТУ им. Н. Э. Баумана, 2003. - 440 с.
Зойтендейк Г. Методы возможных направлений. - М.: ИЛ, 1963. – 175 с.
Методы возможных направлений [Электронный ресурс]. – Режим доступа: http://iasa.org.ua/lections/iso/6/6.5.htm.
Методы математического программирования в задачах оптимизации сложных технических систем: учебное пособие / А.М. Загребаев, Н.А. Крицына, Ю.П. Кулябичев, Ю.Ю. Шумилов. – М.: МИФИ, 2007. – 332 с.
Нурминский Е.А. Методы оптимизации: Курс лекций [Электронный ресурс]. – Режим доступа: http://elis.dvo.ru/nurmi/edu/optimization.pdf.

1 Зойтендейк Г. Методы возможных направлений. - М.: ИЛ, 1963. – 175 с.

2 Методы математического программирования в задачах оптимизации сложных технических систем: учебное пособие / А.М. Загребаев, Н.А. Крицына, Ю.П. Кулябичев, Ю.Ю. Шумилов. – М.: МИФИ, 2007. С. 226-228.

3 Аттетков А.В., Галкин С.В., Зарубин В.С. Методы оптимизации: Учеб. для вузов / Под ред. B.C. Зарубина, А. П. Крищенко. - М.: МГТУ им. Н. Э. Баумана, 2003. С. 387-389.

4 Методы возможных направлений [Электронный ресурс]. – Режим доступа: http://iasa.org.ua/lections/iso/6/6.5.htm.

5 Нурминский Е.А. Методы оптимизации: Курс лекций [Электронный ресурс]. – Режим доступа: http://elis.dvo.ru/nurmi/edu/optimization.pdf.

6 Нурминский Е.А. Методы оптимизации: Курс лекций [Электронный ресурс]. – Режим доступа: http://elis.dvo.ru/nurmi/edu/optimization.pdf.

7 Методы возможных направлений [Электронный ресурс]. – Режим доступа: http://iasa.org.ua/lections/iso/6/6.5.htm.

8 Нурминский Е.А. Методы оптимизации: Курс лекций [Электронный ресурс]. – Режим доступа: http://elis.dvo.ru/nurmi/edu/optimization.pdf.