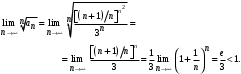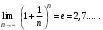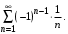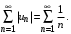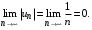Государственное бюджетное профессиональное образовательное учреждение
Уфимский колледж отраслевых технологий
Ряды
Методическая разработка занятия
по дисциплине «Математика»
согласовано:
Методист
_________
«___»________2022 г.
|
Рассмотрено на заседании ЦК ____________________________________
Протокол № __ от «___»________2022 г.
Председатель _________ _______________
|
Содержание
1
2
|
ВВЕДЕНИЕ……………………………………………………………………...
информационная карта занятия………………………………......
|
|
3
|
план и регламент занятия…………………………………………….
|
|
4
5
|
план-конспект занятия…………………...............................................
Приложения…………………...………………………………………….....
|
|
Введение
Тема «Ряды» изучается на 2 курсе по дисциплине «Математика»
Актуальность темы урока связана с возможностью обеспечения полноценной деятельности обучающихся на уроке.
Структура занятия соответствует требованиям ФГОС СПО по специальности 19.02.05 «Технология бродильных производств и виноделие».
Содержание занятия отвечает структуре рабочей программы «Математика» по специальности 19.02.05 «Технология бродильных производств и виноделие» (2курс обучения).
1.Информационная карта занятия
Тема занятия: Ряды
Тип занятия: изучение нового материала
Вид занятия: лекция
Цель занятия: Числовые ряды. Необходимое условие сходимости ряда. Признаки сходимости рядов с неотрицательными членами.
Задачи занятия:
Обучающая:
Освоить основные знания по теме «Ряды»
Продемонстрировать методы решения выражений, содержащих ряды.
Сформировать умения решать выражения, содержащие ряды.
Развивающая:
Способствовать развитию познавательной активности, логического мышления.
Развивать навыки самостоятельной работы.
Развивать навыки самоконтроля.
Воспитательная:
Способствовать воспитанию активности, ответственного отношения к работе, самостоятельности.
Планируемые результаты обучения:
Формируемые компетенции:
OK 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.
ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.
ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий.
ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.
ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности.
Требования к знаниям:
обучающиеся систематизируют знания по теме пределы;
обучающиеся получат знания о теории рядов
Требования к умениям:
- обучающиеся научатся определять сходимость ряда;
- обучающиеся научатся исследовать ряд на сходимость;
- обучающиеся освоят умения определять методы решения выражений, содержащих ряды
Оборудование и оснащение занятия:
1) доска
2) план – конспект урока;
Межпредметные связи: тема «Ряды» связана с курсом атомной и ядерной физики
Предметные связи: тема «Ряды» связана с углубленным изучением темы пределы, дифференцирование функции, а также алгебраической и геометрической прогрессией, изучаемыми на 1 курсе
Методы, приемы и технологии, применяемые на уроке: информационный, частично-поисковый
Продолжительность занятия: 70 минут
Литература:
1. Данко, П. Е. Высшая математика в упражнениях и задачах. Ч. 2 / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. – М. : Высш. шк., 2010.
2. Руководство к решению задач по высшей математике. Ч. 2 / под общ. ред. Е. И. Гурского. – Минск : Высш. шк., 1990.
3. Сборник индивидуальных заданий по высшей математике. Ч. 3 / под ред. А. П. Рябушко. – Минск : Вышейшая школа, 1990.
4. Кузнецов, Л. А. Сборник заданий по высшей математике (типовые расчеты) / Л. А. Кузнецов. – М. : Высш. шк., 2014.
5. Гусак, А. А. Справочное пособие к решению задач : Математический анализ и дифференциальные уравнения / А. А. Гусак. – Минск : ТетраСистемс, 2008.
6. Берман, Г. Н. Сборник задач по курсу математического анализа / Г. Н. Берман. – М. : Наука, 2015.
2.План и регламент занятия
2.1 План занятия
I. Организационная часть.
1) Организационный этап.
2) Приветствие
3) Перекличка
II. Основная часть.
1) Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
2) Актуализация знаний.
3) Озвучивание темы занятия.
4) Озвучивание предметных связей, взаимосвязь с предыдущими темами
5) Изучение нового материала (лекция)
6) Разбор примеров
III. Заключительная часть.
1) Домашнее задание. Инструктаж по выполнению.
2) Подведение итогов занятия. Рефлексия.
2.2. Регламент занятия
Этапы занятия
|
I
|
1)
|
2)
|
3)
|
II
|
1)
|
2)
|
3)
|
4)
|
5)
|
6)
|
III
|
1)
|
2)
|
Минуты
|
6
|
1
|
2
|
3
|
60
|
5
|
5
|
2
|
3
|
30
|
15
|
4
|
2
|
2
|
Время
|
0-6
|
0-1
|
1-3
|
4-6
|
6-66
|
6-11
|
11-16
|
16-18
|
18-21
|
21-51
|
51-66
|
66-70
|
66-68
|
68-70
|
3. План-конспект занятия
I. Организационная часть
1) Организационный этап (1 мин)
2) Приветствие (2 мин)
Добрый день, уважаемые студенты! Сегодня нам с вами предстоит изучить новый материал.
3) Перекличка (3 мин)
Прежде, чем мы приступим к изучению новой темы, давайте отметим, кто из студентов вашей группы отсутствует.
II. Основная часть.
Постановка цели и задач урока. Мотивация учебной деятельности учащихся (5 мин)
Сегодня у нас занятие лекционного типа и связано с получением новой информации. Мы с вами приступаем к изучению нового раздела, относящегося к разделу математического анализа, элементы которого вы изучаете на 2 курсе.
Цели на сегодняшнее занятие таковы:
- познакомиться с основными понятиями числовых рядов.
- познакомиться с основными признаками сходимости рядов.
- рассмотреть примеры решения выражений, содержащих ряды.
Актуализация знаний (5 мин)
На доске записаны две последовательности чисел:
1; 5; 25;125; 625; 3025…
Определить принцип построения числового ряда.
Давайте вместе сделаем вывод. Мы выяснили, что числа, записанные в каждом ряду, представляют собой степень некоторого положительного числа, не равного 1. Подобный тип выражений вы изучали на первом курсе и назывались они степенными или показательными. Как вы считаете, можно ли записать это одним общим выражением? (можно ах = b).
Но данные выражения хороши лишь для конечного числа членов последовательности. Если количество членов в последовательности неизвестно, то стандартные методы решения показательных уравнений не работают. Тут нам на помощь придут способы нахождения дифференциала функции (или по другому производной).
Озвучивание темы занятия (2 мин)
Таким образом мы плавно подходим к теме нашего сегодняшнего занятия, а именно «Ряды». В некоторых учебниках данная тема называется «Числовые ряды».
Озвучивание предметных связей, взаимосвязь с предыдущими темами (3 мин)
В курсе математического анализа, который вы изучаете в этом семестре, присутствует тема, которая исторически была тесно связана с атомной и ядерной физикой. Однако в современном мире знания по данной теме применяются при разработке искусственного интеллекта, в программной инженерии, а также в биомедицинских системах и технологиях. Поскольку нашу современная жизнь невозможно без использования информационных технологий, то данная тема приобрела широкое распространение в различных видах программного обеспечения.
Изучение нового материала (лекция) (30 мин)
Основные понятия Если каждому натуральному числу 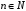 поставлено в соответствие некоторое вполне определенное число поставлено в соответствие некоторое вполне определенное число 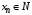 , то говорят, что задана числовая последовательность. , то говорят, что задана числовая последовательность.
Числовую последовательность обозначают

Число 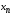 называют называют 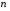 -м членом последовательности, а формулу -м членом последовательности, а формулу 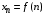 формулой общего члена последовательности. формулой общего члена последовательности.
Числовую последовательность можно рассматривать как числовую функцию, определенную на множестве натуральных чисел.
Пусть задана числовая последовательность
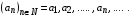
Определение. Выражение вида
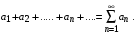 (1) (1)
называется числовым рядом, числа 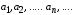 членами ряда, а число членами ряда, а число 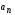 общим (n-м) членом ряда. общим (n-м) членом ряда.
Сумма конечного числа 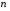 первых слагаемых числового ряда называется первых слагаемых числового ряда называется 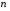 -й частичной суммой данного ряда -й частичной суммой данного ряда
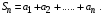
Таким образом, с каждым рядом связана последовательность частичных сумм 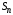
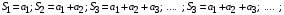 (2) (2)
Если последовательность 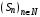 частичных сумм ряда (1) имеет конечный предел частичных сумм ряда (1) имеет конечный предел  , то ряд называется сходящимся, а число S суммой данного ряда: , то ряд называется сходящимся, а число S суммой данного ряда:
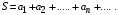
Если предел последовательности 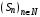 не существует или равен бесконечности, то ряд называется расходящимся. не существует или равен бесконечности, то ряд называется расходящимся.
Выражение вида 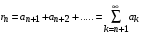 называется n-м остатком ряда (1). называется n-м остатком ряда (1).
Для того чтобы ряд (1) сходился необходимо и достаточно, чтобы остаток ряда стремился к нулю при  : :
 (3) (3)
Необходимый признак сходимости ряда. Если ряд 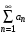 сходится, то сходится, то
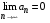 (4) (4)
Заметим, что из выполнения условия (4) не обязательно следует сходимость ряда (1). Но если условие (4) не выполняется, т. е. предел 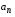 при при  не равен нулю или не существует, то ряд (1) расходится. не равен нулю или не существует, то ряд (1) расходится.
Таким образом, можно сформулировать достаточный признак расходимости ряда: Если предел общего члена ряда не равен нулю или не существует, то ряд расходится. (Пример1)
Свойства сходящихся числовых рядов сформулируем в виде теорем:
Теорема 1. Перестановка, отбрасывание или добавление конечного числа членов ряда не влияет на его сходимость (расходимость.)
Теорема 2. Если ряды  и и 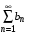 сходятся, и их суммы равны сходятся, и их суммы равны 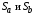 , соответственно, то ряд , соответственно, то ряд  также сходится и также сходится и 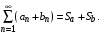
Теорема 3. Если ряд 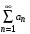 сходятся, и его сумма равна S, то ряд сходятся, и его сумма равна S, то ряд  также сходится и также сходится и 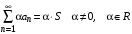 , ,
(Пример2)
Рассмотрим числовой ряд 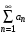 с неотрицательными членами с неотрицательными членами 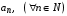 и сформулируем достаточные признаки сходимости этого ряда. и сформулируем достаточные признаки сходимости этого ряда.
2. Интегральный признак Коши.
Если неотрицательная, интегрируемая функция 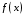 на промежутке на промежутке 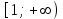 монотонно убывает, и члены ряда монотонно убывает, и члены ряда 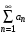 имеют вид имеют вид  то ряд то ряд 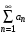 и несобственный интеграл и несобственный интеграл 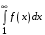 сходятся или расходятся одновременно. сходятся или расходятся одновременно.
(Пример 3)
3. Признак Даламбера (Д ‘Аламбера)
Пусть для ряда 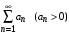 существует предел существует предел
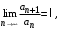 (5) (5)
тогда:
1) при < 1, ряд 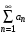 сходится; сходится;
2) при > 1, ряд 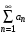 расходится; расходится;
3) при = 1, вопрос о сходимости данного ряда остается открытым.
(Пример 4)
4. Признак сравнения
Если для членов ряда 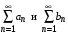 справедливо неравенство справедливо неравенство 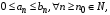 то: то:
1) из сходимости ряда 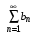 следует сходимость ряда следует сходимость ряда 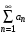 ; ;
2) из расходимости ряда 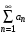 следует расходимость ряда следует расходимость ряда 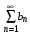 . .
Предельный признак сравнения
Пусть даны знакопеременные ряды 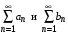 . Если существует конечный и отличный от нуля . Если существует конечный и отличный от нуля 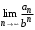 , то оба ряда сходятся или расходятся одновременно. , то оба ряда сходятся или расходятся одновременно.
При использовании признаков сравнения (III, IV) в каждом конкретном случае необходимо найти соответствующий вспомогательный ряд, про который точно известно, сходится он или нет. В качестве таких рядов, используемых для сравнения, выбирают обычно:
Обобщенный гармонический ряд 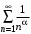 сходится при сходится при 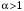 и расходится при и расходится при 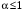 ; ;
Ряд, из элементов геометрической прогрессии 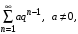 сходящийся при сходящийся при 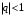 и расходящийся при и расходящийся при 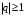 . (Пример 5) . (Пример 5)
Предельный признак Коши.
Пусть для ряда 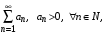 существует предел существует предел 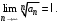 (6) (6)
Тогда
1) при < 1 ряд 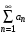 сходится; сходится;
2) при > 1 ряд 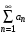 расходится; расходится;
3) при = 1 вопрос о сходимости данного ряда остается открытым.
Ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными. Частным случаем знакопеременных рядов являются знакочередующиеся ряды, т. е. такие ряды, все члены которых поочередно меняют знак.
Знакочередующийся ряд может быть записан так
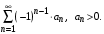 (7) (7)
Пусть дан знакопеременный ряд 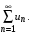 Тогда ряд, составленный из модулей членов данного ряда Тогда ряд, составленный из модулей членов данного ряда 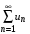 , является знакоположительным рядом. , является знакоположительным рядом.
Теорема. Если сходится ряд 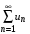 , то сходится и ряд , то сходится и ряд 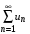
Для знакочередующегося ряда 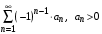 имеет место следующая теорема (признак Лейбница): имеет место следующая теорема (признак Лейбница):
Если член знакочередующегося ряда (7) удовлетворяет условиям:
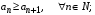
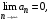
то ряд сходится, а его сумма S не превосходит первого члена, т.е. 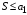 . .
Определение. Если сходится ряд 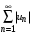 , то ряд , то ряд 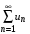 называется абсолютно сходящимся. Если ряд называется абсолютно сходящимся. Если ряд 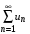 сходится, а ряд сходится, а ряд 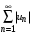 расходится, то ряд расходится, то ряд 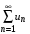 называется условно сходящимся. называется условно сходящимся.
Исследование знакочередующегося ряда на сходимость начинают с проверки на абсолютную сходимость. Если ряд, составленный из модулей членов ряда, расходится, применяют признак Лейбница. (Пример 7)
6) Разбор примеров (15 мин)
Пример 1. Исследовать на сходимость ряд 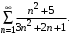
Решение. Общий член данного ряда 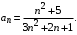
Найдем предел 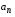 при при  : :
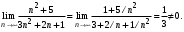
Следовательно, данный ряд расходится.
Пример 2. Рассмотрим ряд, составленный из элементов геометрической прогрессии со знаменателем 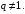
Исследовать на сходимость ряд
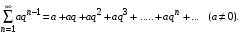
Решение. Найдем сумму 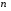 первых членов ряда первых членов ряда
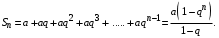
Учитывая, что 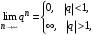 найдем предел найдем предел 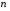 ой частной суммы при ой частной суммы при  : :

Следовательно, данный ряд сходится при  , и его сумма равна , и его сумма равна 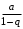 . .
При  ряд имеет вид: ряд имеет вид: 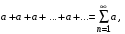 а а
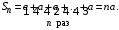
Тогда 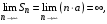 поэтому ряд расходится. поэтому ряд расходится.
При 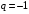 получаем ряд: получаем ряд:
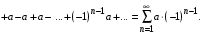
Данный ряд расходится, так как последовательность частичных сумм:  не имеет предела. не имеет предела.
Пример 3. Исследовать на сходимость обобщенный гармонический ряд
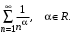
Решение. Исследование данного ряда начнем с необходимого признака сходимости:
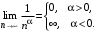
Таким образом, при 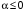 данный ряд расходится, т.к. нарушается необходимое условие сходимости. данный ряд расходится, т.к. нарушается необходимое условие сходимости.
Пусть  . Рассмотрим . Рассмотрим 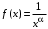
Функция 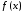 монотонно убывает на промежутке монотонно убывает на промежутке 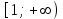 . Найдем несобственный интеграл. . Найдем несобственный интеграл.
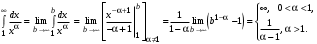
При 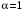
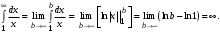
Следовательно, обобщенный гармонический ряд 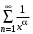 сходится при сходится при 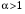 и расходится при и расходится при 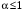 . .
Пример 4. Исследовать на сходимость ряд
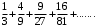
Решение. Общий член данного ряда имеет вид 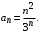
Тогда, 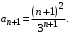 Найдем предел Найдем предел
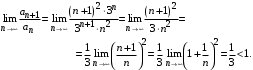
Следовательно, данный ряд сходится по признаку Д 'Аламбера.
Пример 5. Исследовать на сходимость ряд 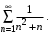
Решение. Рассмотрим ряд с общим членом 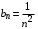 . Этот ряд сходится, т.к. является обобщенным гармоническим рядом при . Этот ряд сходится, т.к. является обобщенным гармоническим рядом при 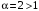 . .
Найдем 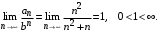
Ряд 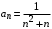 сходится, так как сходится ряд сходится, так как сходится ряд 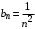 . .
Пример 6. Исследовать сходимость ряда
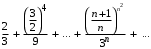
Решение. Общий член данного ряда имеет вид 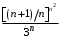 . Найдем . Найдем
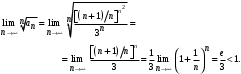
Следовательно, ряд сходится.
В этом примере был использован второй замечательный предел
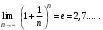
Пример 7. Исследовать на сходимость ряд 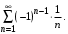
Решение. Составим ряд из модулей 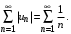 Получим гармонический ряд, который расходится. Проверим признак Лейбница:
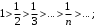
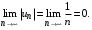
Оба условия выполняются, следовательно, ряд сходится условно.
III. Заключительная часть.
Домашнее задание. Инструктаж по выполнению.
Сейчас записываем домашнее задание. Основное задание прикреплено в Дневник.ру и оно состоит в следующем: используя материалы лекции, прикрепленные к уроку ответьте на вопросы из раздела домашнего задания и подготовьте устные ответы по ним, т.к. на следующем занятии будет выборочный опрос.
1. Дайте определение ряда и его частичных сумм.
2. Дайте определение сходящейся последовательности.
3. Сформулируйте необходимый признак сходимости рядов.
4. Сформулируйте достаточный признак расходимости рядов, исходя из необходимого условия сходимости рядов.
5. Сформулируйте свойство линейности сходящихся рядов.
2) Подведение итогов занятия. Рефлексия.
Уважаемые студенты, на этом наше занятие завершается, если есть ко мне вопросы, то вы можете их задавать.
|
 Скачать 226.06 Kb.
Скачать 226.06 Kb.
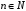 поставлено в соответствие некоторое вполне определенное число
поставлено в соответствие некоторое вполне определенное число 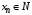 , то говорят, что задана числовая последовательность.
, то говорят, что задана числовая последовательность.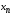 называют
называют 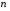 -м
-м 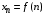 формулой общего члена последовательности.
формулой общего члена последовательности.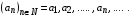
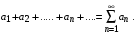 (1)
(1)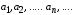 членами ряда, а число
членами ряда, а число 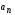 общим (n-м) членом ряда.
общим (n-м) членом ряда.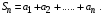
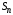
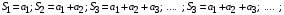 (2)
(2)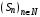 частичных сумм ряда (1) имеет конечный предел
частичных сумм ряда (1) имеет конечный предел 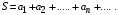
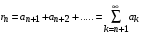 называется n-м остатком ряда (1).
называется n-м остатком ряда (1).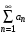 сходится, то
сходится, то 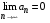 (4)
(4)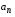 при
при  и
и 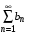 сходятся, и их суммы равны
сходятся, и их суммы равны 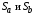 , соответственно, то ряд
, соответственно, то ряд  также сходится и
также сходится и 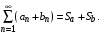
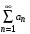 сходятся, и его сумма равна S, то ряд
сходятся, и его сумма равна S, то ряд  также сходится и
также сходится и 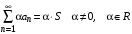 ,
, 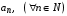
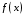 на промежутке
на промежутке 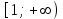 монотонно убывает, и члены ряда
монотонно убывает, и члены ряда 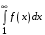 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.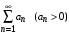 существует предел
существует предел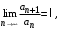 (5)
(5)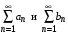 справедливо неравенство
справедливо неравенство 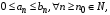 то:
то: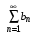 следует сходимость ряда
следует сходимость ряда 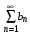 .
.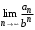 , то оба ряда сходятся или расходятся одновременно.
, то оба ряда сходятся или расходятся одновременно.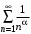 сходится при
сходится при 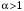 и расходится при
и расходится при 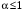 ;
;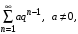 сходящийся при
сходящийся при 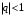 и расходящийся при
и расходящийся при 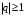 . (Пример 5)
. (Пример 5)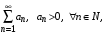 существует предел
существует предел 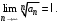 (6)
(6) 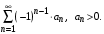 (7)
(7)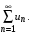 Тогда ряд, составленный из модулей членов данного ряда
Тогда ряд, составленный из модулей членов данного ряда 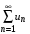 , является знакоположительным рядом.
, является знакоположительным рядом.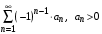 имеет место следующая теорема (признак Лейбница):
имеет место следующая теорема (признак Лейбница): 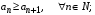
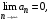
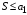 .
. 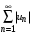 , то ряд
, то ряд 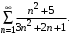
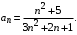
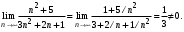
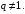
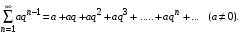
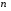 первых членов ряда
первых членов ряда 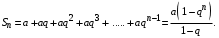
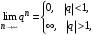 найдем предел
найдем предел 
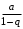 .
.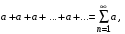 а
а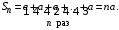
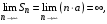 поэтому ряд расходится.
поэтому ряд расходится.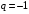 получаем ряд:
получаем ряд: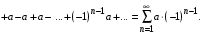
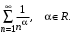
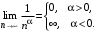
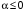 данный ряд расходится, т.к. нарушается необходимое условие сходимости.
данный ряд расходится, т.к. нарушается необходимое условие сходимости.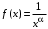
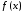 монотонно убывает на промежутке
монотонно убывает на промежутке 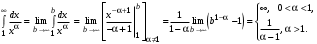
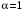
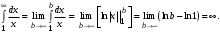
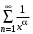 сходится при
сходится при 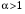 и расходится при
и расходится при 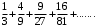
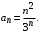
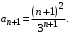 Найдем предел
Найдем предел 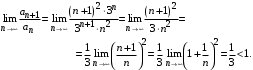
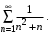
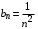 . Этот ряд сходится, т.к. является обобщенным гармоническим рядом при
. Этот ряд сходится, т.к. является обобщенным гармоническим рядом при 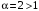 .
.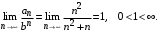
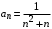 сходится, так как сходится ряд
сходится, так как сходится ряд 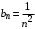 .
.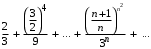
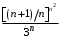 . Найдем
. Найдем