Методичка энергоцепи. Методичка для курсовика 2019(рус). Методические рекомендации для выполнения курсовой работы по дисциплине Энергетические цепи Для заданной преподавателем схемы экспериментальной установки, описать принцип ее работы,
 Скачать 102.47 Kb. Скачать 102.47 Kb.
|
|
Методические рекомендации для выполнения курсовой работы по дисциплине «Энергетические цепи» Для заданной преподавателем схемы экспериментальной установки, описать принцип ее работы, выбрать наиболее ее характерные режимы, составить для них энергетические цепи и исследовать их на основе частотных характеристик. Примерный перечень тем: схема устройства для согласования энергетических процессов (демпфера, фильтра и т.п.); схема колебательного привода змеевика емкостного теплообменника. схема привода мембранного нагнетателя для объектов малой энергетики с ускорением на всасывании (нагнетании); схема смесительного устройства для объектов малой энергетики с мембранным насосом; схема корректирующий контур для объектов малой энергетики с мембранным насосом. В качестве задания на курсовую работу может быть схема экспериментальной установки выпускной квалификационной работы (ВКР). План курсовой работы. Введение. Описание проблемы, касающейся данной работы и путей ее решения (из анализа литературных источников). Разработка схемы экспериментальной установки и подробное ее описание принципа работы. Составление энергетической цепи установки (для гидравлики, теплопередачи) с описанием отдельных звеньев. Математические преобразования энергетической цепи с получением комплексных сопротивлений, частотной функции, амплитудно-частотной и фазочастотной характеристики. Построение частотных характеристик цепи при изменении не менее трех параметров. Анализ полученных частотных характеристик и технического результата данной схемы установки. Методические рекомендации к выполнению работы 1. Во введении приводится актуальность данной работы, цель и задачи исследования, структура работы, используемые методы и конечные результаты. Например, актуальностью работы может быть более совершенная математическая модель, позволяющая описать ранее неизученные режимы работы установки, учесть важнейшие конструктивные параметры, повысить точность прогноза нахождения входных (выходных) фазовых переменных. Задачи работы должны быть согласованы с заданием. Например, описать проблему и определить пути ее решения, разработать схему экспериментальной установки и сделать ее описание… 2. При разработке схемы экспериментальной установки необходимо руководствоваться принципами: схема должна не сложной; она должна воспроизводить интересующие разработчика режимы; в схеме должны использоваться по возможности стандартные общедоступные элементы. Не стандартные элементы (ударные клапаны, мембранные нагнетатели, проточные кавитаторы и т.п.) должны иметь отличительные признаки от предшественников. В частности для ударного клапана можно изменить материал тарелки клапана, конструкцию опор, тип пружин и т.п. Описание функциональной (принципиальной) схемы следует делать по алгоритму. Приводится сама схема (рис.1), показывается состав элементов и принцип ее работы. Позиционные обозначения должны строго соответствовать порядку процесса работы. Пример с диафрагменным нагнетателем. 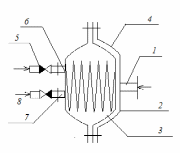 Рис. 1. Схематическое изображение диафрагменного нагнетателя: 1- входной патрубок; 2- диафрагма; 3- пружина; 4- корпус; 5, 8- обратный клапан; 6- нагнетательный патрубок; 7- выходной патрубок При подаче импульса давления к входному патрубку 1, он будет воздействовать на диафрагму 2, которая сместится влево, сдавливая пружину 3. При перемещении диафрагмы 2 она будет вытеснять жидкость, расположенную в корпусе 4 через обратный клапан 5, соединенный с нагнетательным патрубком 6. Впускной патрубок 7 соединен с обратным клапаном 8. При прекращении импульса давления диафрагма 2 под действием пружины 3 переместится вправо, а ее полость в корпусе 4 будет заполняться новой порцией жидкости через обратный клапан 8. 3. Энергетическая цепь необходима для удобства составления дифференциальных уравнений конкретного процесса в установке. Не следует пытаться составить энергетическую цепь для всей установки, это очень сложная задача и практически не осуществимая. Во-первых, необходимо выбрать нужный процесс для исследования (гидродинамика, теплопередача, электричество и др.), во-вторых определить контрольные точки на схеме (начало и конец процесса). При исследовании процесса в установке с помощью энергетической цепи необходимо придерживаться алгоритма. Алгоритм исследования процессов с использованием энергетических цепей состоит из шагов 1) Исходя из интересующего процесса определяется тип отдельных звеньев и их количество. Например, для энергетической цепи мембранного насоса: первое звено гидравлическое, второе механическое и третье гидравлическое. В этом случае будут три комплексных сопротивления. Если вас интересует единая цепь, то необходимы еще два преобразовательных звена, первое будет связывать гидравлику и механику, а второе наоборот механику и гидравлику. Таким образом, единая энергетическая цепь будет включать пять звеньев (рис 2) и в конце будет только одно комплексное сопротивление.  Рис. 2. Энергетическая цепь диафрагменного нагнетателя Первое звено гидравлическое, учитывает падение давления на входе при изменении диаметров активным сопротивлением 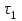 , массу воды в приемной камере , массу воды в приемной камере 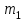 , податливость диафрагмы , податливость диафрагмы 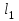 ; второе звено – преобразовательное, преобразует давление ; второе звено – преобразовательное, преобразует давление 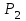 и объемный расход и объемный расход 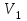 в силу fи скорость в силу fи скорость 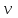 ; третье звено – механическое – учитывает потери на трение диафрагмы активным сопротивлением ; третье звено – механическое – учитывает потери на трение диафрагмы активным сопротивлением 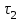 , массой подвижных частей , массой подвижных частей 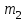 , податливые свойства диафрагмы податливостью , податливые свойства диафрагмы податливостью 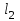 ; четвертое звено – преобразователь – преобразует силу f2и скорость ; четвертое звено – преобразователь – преобразует силу f2и скорость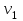 в давление в давление 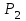 и объемный расход и объемный расход 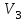 ; пятое звено – гидравлическое, учитывает упругие свойства диафрагмы податливостью ; пятое звено – гидравлическое, учитывает упругие свойства диафрагмы податливостью 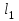 , объем воды в нагнетательной камере массой , объем воды в нагнетательной камере массой 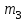 и сопротивление выпуска, активным сопротивлением и сопротивление выпуска, активным сопротивлением 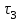 . .2) Формируются конкретные звенья. Необходимо помнить, что в каждой энергетической системе (электричество, механика, гидравлика, акустика, тепло) только три элемента и их включение в цепь подчиняется аналогиям. Например, аналогом электрического активного сопротивления являются: поступательное активное сопротивление в механической поступательной цепи, вращательное механическое сопротивление во вращательной цепи, гидравлическое активное сопротивление в гидравлической цепи, тепловое активное сопротивление в тепловой цепи. Это все активные сопротивления, так как на них происходит рассеивание (диссипация) энергии в окружающую среду. Вторая группа сопротивлений – инерционные (индуктивность, масса, момент инерции, гидравлическая масса). В этих элементах происходит накопление энергии в зависимости от величины изменения фазовой переменной типа тока (скорости, угловой скорости, объемного расхода, теплового потока). Третья группа элементов – накопительные (электрическая емкость, податливость в механической поступательной цепи, податливость в механической вращательной цепи, податливость в гидравлической цепи, теплоемкость в тепловой цепи). Это группа звеньев также накапливает и отдает энергию. На преобразовательных звеньях не происходит потерь энергии, они подчиняются реальным физическим законам (Ома, Фурье, Гука и т.п.). Каждое принятое звено должно сопровождаться описанием. Например, активное сопротивление в гидравлической цепи учитывает, трение потока о стенки трубы, инерционное сопротивление учитывает инерционные свойства воды, податливость учитывает сжатие воды и стенок трубопроводов. 3) Записываются уравнения звеньев. Как правило, звенья записывают с лева направо, но можно и наоборот. Для каждого звена составляются два уравнения: типа напряжения и типа тока. Большинство звеньев имеют линейную зависимость, кроме гидравлики. В гидравлике падение давления на активном сопротивлении имеет квадратическую зависимость от расхода. Это обусловлено квадратическим законом трения для развитого турбулентного течения. Поэтому первым шагом в преобразованием уравнений является их линеризация, поскольку преобразование Лапласа распространяется только на линейные уравнения. Уравнения звеньев цепи для рисунка 2 будут выглядеть следующим образом. Уравнения звеньев цепи для рис.2: 1) 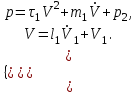 2) 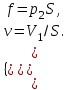 3) 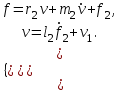 4) 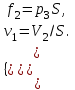 5) 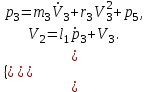 4) Но прежде чем приступить к линеризации звеньев, если таковые имеются, необходимо определиться с входом и выходом энергетической цепи. У разомкнутой цепи есть правый и левый край. Вход и выход можно назначить как для левого, так и правого края. Здесь руководствуются правилом «черного ящика». За выходную фазовую переменную берут ту, которую можно подтвердить экспериментально, как правило, это может быть напряжение (давление, угловая скорость, линейная скорость, температура). Сложные уравнения в большинстве случаев составляют на приращения, то есть входную и выходную фазовые переменные представляют в виде постоянной составляющей и отклонения. Данный прием позволяет учесть в конечных уравнениях постоянные составляющие фазовых переменных. Одним из приемов линеризации является пренебрежение квадратом , т.е. 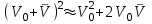 . .5) Когда определились с входом и выходом цепи приступают к преобразованиям уравнений. Целью данного преобразования является получить связь фазовых переменных (типа напряжения и тока) в начале цепи с ее конечными фазовыми переменными, причем в данные уравнения не должны входить промежуточные переменные. Преобразование можно выполнять, как справа налево, так и наоборот. В большинстве случаев идут справа на лево. В ряде случаев единой цепи не требуется и тогда каждое звено заканчивается комплексным сопротивлением и из них находят эквивалентное комплексное сопротивление цепи. В некоторых случаях в ходе преобразований можно столкнуться с громоздкими выражениями. В этом случае вводят промежуточные коэффициенты, а они затем войдут в окончательные коэффициенты. В итоге должно получиться 2 уравнения, связывающие фазовые переменные (типа напряжения и тока) в начале цепи с их конечными фазовыми переменными. Для дальнейшего анализа достаточно одного уравнения, как правило, это уравнение типа «давления». Конечное уравнение записывают в порядке старших производных слева направо, а параметры собирают в коэффициенты. Например, 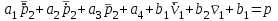 . .6) Полученное в пункте 5 конечное дифференциальное уравнение на приращения записывают на изображения с помощью преобразования Лапласа. Первая производная заменяется на s, вторая на 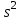 и т.д. Например, и т.д. Например, 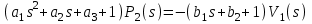 . .7) Записывают комплексное сопротивление цепи, как отношение изображений выходной переменной к входной, то есть 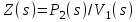 . В случае если у каждого звена было свое комплексное сопротивление, то находят эквивалентное комплексное сопротивлении, как в электрических цепях с учетом последовательного и параллельного соединения. Например, . В случае если у каждого звена было свое комплексное сопротивление, то находят эквивалентное комплексное сопротивлении, как в электрических цепях с учетом последовательного и параллельного соединения. Например, 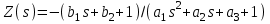 . .8) Записывают частотную функцию цепи путем замены комплексной переменной 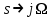 . . 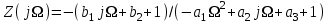 . .Здесь 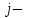 мнимая единица, мнимая единица, 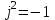 , , 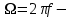 круговая частота, рад/c. Из частотной функции находят действительную и мнимые части. Для этого числитель и знаменатель умножают на комплексно-сопряженную функцию, например круговая частота, рад/c. Из частотной функции находят действительную и мнимые части. Для этого числитель и знаменатель умножают на комплексно-сопряженную функцию, например 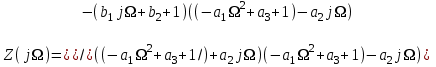 Действительная часть частотной функции: Действительная часть частотной функции: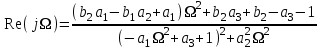 . .Мнимая часть частотной функции: 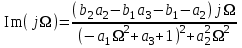 . .9) Определяют параметры и коэффициенты, энергетической цепи. Это одна из самых ответственных операций данного алгоритма. Параметры энергетической цепи можно установить как экспериментальным, так и расчетным путем. На начальном этапе параметры определяют расчетным путем. Для этого задаются входной мощностью, а далее на каждом сопротивлении устанавливают долю ее падения исходя их практических соображений. Например, потери мощности на трение в подшипниках качения (скольжения) принимают не более 5%, потери мощности на трение в трубопроводах не более 10%. Массу и момент инерции можно определить пользуясь законами механики. Наибольшую сложность представляет определение различных видов податливостей, поскольку в них входят производные силы, момента, давления заранее угадать которые очень сложно. В реальных динамических системах производные силы, момента, давления могут в несколько раз отличаться от текущих значений. Более точные расчеты параметром получают по экспериментальным данным. В качестве примера можно привести определение податливости потока жидкости в момент закрытия ударного клапана. Для этого необходимо знать превышение давления при резком закрытии клапана и заданное значение расхода. Определяют параметры в строгом соответствии с уравнениями, записанными в п.3. 10) Рассчитывают частотные характеристики энергетической цепи: - амплитудно-частотная характеристика цепи (АЧХ), определяется по выражению 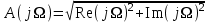 ; ;- фаза-частная характеристика энергетической цепи (ФЧХ) 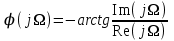 . .Расчет АЧХ и ФЧХ ведут, как правило, на компьютере. Для этого минимально задаются 10 значениями, например 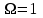 , 2, 3…10. Далее смотрят на график АЧХ, на этом графике по оси Y должна быть видна цифра 1. Цифра 1 является пограничной, значения АЧХ меньше 1 означают ослабление сигнала выходной переменной, а больше 1 усиление сигнала. , 2, 3…10. Далее смотрят на график АЧХ, на этом графике по оси Y должна быть видна цифра 1. Цифра 1 является пограничной, значения АЧХ меньше 1 означают ослабление сигнала выходной переменной, а больше 1 усиление сигнала. 11) Анализируют полученные частотные характеристики. В первую очередь анализируют АЧХ, поскольку она несет информации больше. Перед началом анализа необходимо помнить, что вы хотите узнать реакцию рассматриваемой динамической системы (ее формализация энергетическая цепь) на единичное входное воздействие 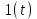 . Динамическая система может усилить, ослабить или оставить на прежнем уровне выходную переменную, то есть речь идет о неком фильтре (верхних или нижних частот, полосовой). Здесь необходимо выяснить это. . Динамическая система может усилить, ослабить или оставить на прежнем уровне выходную переменную, то есть речь идет о неком фильтре (верхних или нижних частот, полосовой). Здесь необходимо выяснить это.ФЧХ показывает запаздывание выхода по отношению к входу. Запаздывание может быть как в положительную сторону, так и в отрицательную. Литература Системы автоматизированного проектирования: В 9-ти кн. Кн. 4. Матеематические модели технических объектов: Учеб. пособие для втузов/ В.А. Трудоношин, Н.В. Пивоварова; Под ред. И. П. Норенкова. – М.: Высш. шк., 1986. – 160 с.: ил. Ольсон Г. Динамические аналогии (перевод с английского) Гос. Из-во Иностранной литературы. –М., 1947. Левцев А. П. Импульсные системы тепло- и водоснабжения : монография/А. П. Левцев, А. Н. Макеев ; под. общ. ред. д-ра техн. наук проф. А. П. Левцева. – Саранск : Изд-во Мордов. ун-та, 2015.- 172 с. Вантюсов Ю.А. Динамика механических цепей сельскохозяйственных агрегатов.– Саратов : Изд-во Сарат. ун-та, 1984.- 202 с. Волков Ю. Д. Информационные технологии в энергетике / Ю.Д. Волков, Ю, А. Вантюсов, А. П. Левцев.- Саранск, 2012.- 220 с. |
