курсовая. Методические рекомендации по применению составленных задач на уроках математики 9 класса
 Скачать 2.32 Mb. Скачать 2.32 Mb.
|
|
Глава 2. Использование свойств, квадратичной функции при решении практико-ориентированных задач в курсе математики 9 класса 2.1 Задачи практической направленности, решаемые с помощью применения свойств, квадратичной функции I. Задачи с использованием физических формул 1.Задача по кинематике. Движение тела вертикально вверх под действием силы тяжести Высоту над землей подброшенного вертикально вверх мяча вычисляют по формуле h(t) = –4t² + 22t, где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее 10 м? Рекомендации: решение квадратного неравенства. Анализируя условие, вы заметили, что для ответа на вопрос необходимо найти промежуток времени, когда камень находился на высоте не менее 10 м, то есть те значения t, при которых h(t) ≥ 10. Решая полученное неравенство –4t² + 22t ≥ 10, получаем t ∈ [0,5; 5]. Длина полученного промежутка равна 5 – 0,5 = 4,5 секунд. Ответ: 4,5 с. 2.Задача по гидростатике. На течение жидкости В боковой стенке высокого цилиндрического бака у самого дна закреплен кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нем, выраженная в метрах, меняется по закону H(t) = H0 - 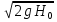 kt + kt + 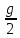 k2t2 где t время в секундах, прошедшее с момента открытия крана, H0 = 20 м – начальная высота столба воды, k = k2t2 где t время в секундах, прошедшее с момента открытия крана, H0 = 20 м – начальная высота столба воды, k = 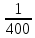 отношение площадей поперечных сечений крана и бака, а g ускорение свободного падения (считайте g = 10 м/c2). Через сколько секунд после открытия крана в баке останется четверть первоначального объёма воды? отношение площадей поперечных сечений крана и бака, а g ускорение свободного падения (считайте g = 10 м/c2). Через сколько секунд после открытия крана в баке останется четверть первоначального объёма воды?Рекомендации : решение квадратного уравнения. Задача сводится к решению уравнения H(t) = 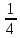 H0 при заданных значениях начальной высоты H0 = 20 м – , отношения площадей поперечных сечений крана и бака k = H0 при заданных значениях начальной высоты H0 = 20 м – , отношения площадей поперечных сечений крана и бака k = 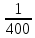 и ускорения свободного падения g = 10 м/c2 : t2 – 1600t + 480000 = 0. Решив квадратное уравнение, имеем 400с и 1200с. 1200 с не удовлетворяет условию задачи. и ускорения свободного падения g = 10 м/c2 : t2 – 1600t + 480000 = 0. Решив квадратное уравнение, имеем 400с и 1200с. 1200 с не удовлетворяет условию задачи. Ответ: 400 с. 3.Раздел «Термодинамика» Зависимость температуры нагревательного элемента от времени имеет вид T(t) = T0 + at + bt2 , где T0 = 100K, a = 37,5 K/мин, b = - 0,25 K/мин2 . Прибор может испортиться при температуре свыше 100 К. Определите момент времени (в минутах), когда прибор необходимо отключить, чтобы он не вышел из строя. Рекомендации. Зависимость температуры нагревательного элемента от времени имеет вид квадратичной функции. Ее графиком является парабола, ветви которой направлены вниз, так как коэффициент при t2 отрицательный. График изменения температуры показан на рис. (см. рис. на слайде.) Таким образом, температура 1000K достигается дважды: первый раз на промежутке возрастания, - второй на промежутке убывания. Но реально до второго раза температура просто не дойдет, так как прибор уже при времени t1 выйдет из строя. Значит, наша цель определить меньший корень уравнения. t1 = 30, t2 = 120. Ответ. 30 4. Давление на дно сосуда. Если достаточно быстро вращать ведeрко с водой на верeвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведeрка сила давления воды на дно не остаeтся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила еe давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна  ,где m — масса воды в килограммах, v — скорость движения ведeрка в м/с, L — длина верeвки в метрах, g — ускорение свободного падения (считайте ,где m — масса воды в килограммах, v — скорость движения ведeрка в м/с, L — длина верeвки в метрах, g — ускорение свободного падения (считайте Рекомендации. Сила воды в верхней точке равна 0. Ответ: 2 м/с 5. Для некоторой реки экспериментально установили следующую зависимость скорости течения реки v(м/с) от глубины h (м) V(t) =- h2+2h+8 Найдите максимальную глубину реки (т.е. глубину, где v=0) и глубину с максимально сильным течением. Решение: (Для решения задачи достаточно выяснить, какое значение -наибольшее или наименьшее - принимает функция. Это значение равно ординате вершины параболы). План решения: Найти вершину (m:n): m=- Ветви направлены- Нули функции По графику ответить на вопросы. 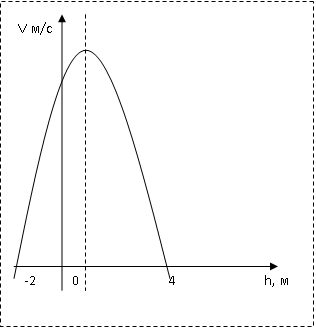 Ответ: v=0, если h=-2 и h=4 т.е. максимальная глубина 4 м. Наибольшая скорость 9 м/с при h=1м. 6. После начала торможения движение электропоезда описывается законом 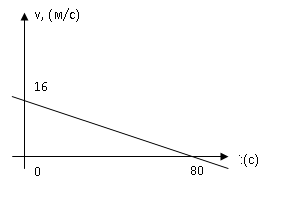 V=16-0,2t-линейная функция 16-0,2t=0 t=80 v=16м/с≈57,8км/ч Поезд проедет 640м через 80с
Вершина x=m=- =80(16-0,1·80)=80·8=640м. нули функции 16t-0,1t2=0 t(16-0,1t)=0 t1=0 16-0,1t=0 -0,1t=-16 t2=160 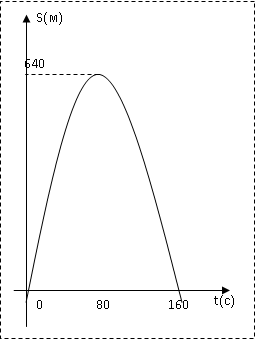 По графикам ответим на вопросы: Через сколько секунд поезд остановится? [ (рис.2) через 80с v поезда=0] Каков его тормозной путь? [После торможения поезд проедет 640м.] Для сравнения автомобиль со скоростью 60км/ч проходит 17м в секунду. Его тормозной путь 3-6 метров!!! 7. Для некоторой реки экспериментально установили следующую зависимость скорости течения реки v(м/с) от глубины h (м) V(h) =- h2+2h+8 Найдите максимальную глубину реки (т.е. глубину, где v=0) и глубину с максимально сильным течением. 8. После начала торможения движение электропоезда описывается законом Через сколько секунд поезд остановится? Каков его тормозной путь? 9. Брошенная на землю кожура от банана в нашем климате разлагается около 2 лет. Брошенный окурок сигареты разлагается на два года дольше. Пластиковый пакет разлагается на восемь лет дольше, чем окурок. Сколько лет потребуется для того чтобы разложился пакет? На сколько лет раньше разложится кожура от банана? (12 лет, на 10лет). 10. Стоимость эксплуатации катера, плывущего со скоростью v км/ч, составляет (90+ ) рублей в час. С какой скоростью должен плыть катер, чтобы стоимость 1 км путь была наименьшей? 11.С башни выпустили вверх стрелу из лука. Если начальная скорость стрелы равна 50 м/с, высота башни 20 м и t – время полёта стрелы (в секундах), то расстояние h (в метрах) стрелы от поверхности земли можно найти по формуле h=-5t2+50t+20 (приближённое значение ускорения свободного падения считается равным с 10 м/с2). Какой наибольшей высоты достигнет стрела? Постройте график движения стрелы по уравнению h= -5t2 +50t+20. Значение t[1;8] c шагом 1. Отметьте точку, в которой стрела достигнет наибольшей высоты. 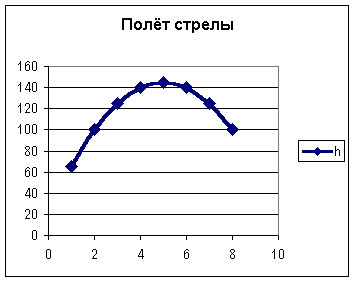 II. Геометрические задачи с использованием квадратичных функций 1. Окно имеет форму прямоугольника, завершенного полукругом. Периметр фигуры равен 6м .Каковы должны быть размеры окна, чтобы окно пропускало наибольшее количество света? Решение: Окно будет обладать наибольшей пропускной способностью, если при заданном периметре будет иметь максимальную площадь. 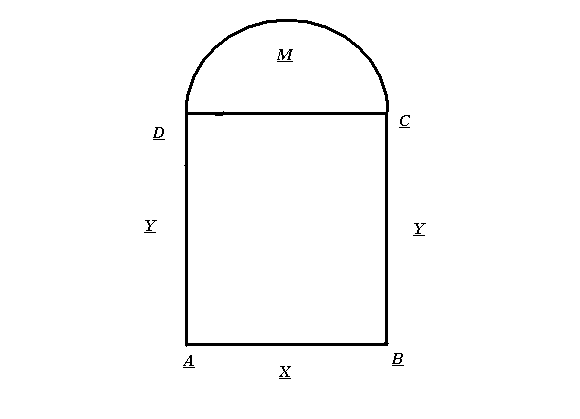 Пусть 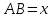 , , 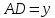 , тогда , тогда 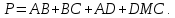 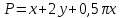 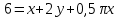 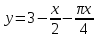 (1) (1) 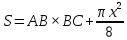 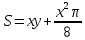 (2) (2) Из (1),(2) следует, что 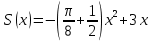 Известно, что квадратный трехчлен принимает наибольшее значение при 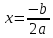 , т.е. , т.е. 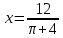 , , 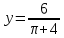 . . Ответ. Размеры окна 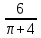 , , 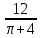 . .Примерно ширина окна 0,8 м, а длина 1,7 м. 2. Сейчас мы с вами рассмотрим ситуацию из рассказа Л.Н. Толстого «Много ли человеку земли надо». Крестьянин Пахом, который мечтал о собственной земле и собрал наконец требуемую сумму, предстал перед требованием старшины: «Сколько за день земли обойдешь, вся твоя будет за 1000 р. Но если к заходу солнца не возвратишься на место, с которого вышел, пропали твои деньги». Прочитать отрывок из собрания сочинений Л.Н. Толстого, том 10, стр. 368. Обошел Пахом четырехугольник (на доске рисунок) периметром 40 км. Наибольшую ли площадь при данном периметре получил Пахом? Решение: Обозначим одну сторону через х , тогда другая сторона будет равна (20 – х). Площадь прямоугольника: = x (20 – x) = - x2 + 20x Функция для нахождения площади будет иметь вид: y = - x2 + 20x. Надо найти наибольшее значение этой функции. Для этого построим график функции. (На доске изображен график этой функции). Мы видим, что наибольшее значение этой функции достигается в вершине параболы, и оно равно 100 при х = 10. Пахом, чтобы получить больше земли, должен был обойти квадрат со стороной 10 км. 3. Зависимость между размером используемой площади полей и валовым доходом из расчета на 100 га угодий лесостепной зоны Львовской области выражена функцией у =9+9х-1,5х2 где х – площадь сельскохозяйственных угодий (в тыс. га), у – валовой доход на 100 га сельскохозяйственных угодий (в тыс. руб.). При какой площади хозяйство будет иметь наибольший доход? 4. Нужно огородить участок прямоугольной формы забором длиной 200м. Каковы должны быть размеры прямоугольника, чтобы его площадь была наибольшей? (Ответ: 50; 50). 5. Периметр здания составляет 56 м. Каковы его стороны, если это здание имеет наибольшую площадь? (здание одноэтажное) (Ответ: 14; 14). 6. На странице книги печатный текст должен занимать 150 см2. Верхнее и нижнее поля страницы по 3 см, правое и левое – по 2 см. если принимать во внимание только экономию бумаги, то каковы должны быть наиболее выгодные размеры страницы? 7. Для строительства склада заготовлен материал на наружные стены длиной 32 м и высотой 4 м. Какими должны быть размеры склада (в виде прямоугольного параллелепипеда), чтобы он имел наибольший объём? Решение задачи сводится к исследованию функции: V = х (16 – х)4 = - (2х – 16)² + 256 ≤ 256, где х – длина. Значит, 2х -16=0, х = 8. Вывод. Итак, чтобы объем склада был наибольшим, его размеры должны быть 8× 8 ×4. 2.2 Методические рекомендации по применению составленных задач на уроках математики 9 класса Основная задача состоит в том, что максимально преодоление недостатков познавательной деятельности, подготовка школьников к жизни и деятельности в новых социально – экономических условиях, получение более широкой, жизненно важной информации для дальнейшего выбора профессии, трудоустройства, свободной ориентировки в современном обществе и быту. Реализация данной задачи невозможна без поиска и совершенствования новых методов, приёмов и средств обучения, в т. ч. и математике. Одним из способов решения проблемы социализации выпускников школ - VIII вида к условиям современной действительности является внедрение в содержание курса математики задач практической направленности – это экономические, профориентационные, социальные и другие типы задач. Использование задач с практическим содержанием способствует обеспечению более осознанного овладения математической теорией и практикой, создает условия для осуществления связи обучения математике с жизнью, развития межпредметных связей и способствует более успешной социализации выпускников в современном обществе. Необходимость в новых подходах к обучению математике и, в частности решению задач, вызвана изменением содержания образования в современной школе с учетом обновления социально-экономических потребностей и условий развития общества. Сущность данного подхода состоит в создании системы работы, основанной на решении задач с практическим содержанием на уроках математики. Идея состоит в том, что использование данных задач способствует обеспечению более осознанного овладения математической теорией и практикой и в дальнейшем окажет влияние на более успешную социализацию выпускников в современном обществе.
Заключение Во время исследования была изучены психолого-педагогические, методические и учебные научные литературы. Определены функции и этапы решения практико-ориентированных задач как основного средства реализации прикладной направленности школьного курса математики. Составлено и подобраны практико-ориентированные задачи, решаемые с помощью использования свойств квадратичной функции. Разработаны методические рекомендации по использованию составленных задач, а так же составлен план экспериментальной работы. Обучение решению практико-ориентированных задач при изучении квадратичной функции в целях реализации прикладной направленности будет способствовать формированию: умения решать практико-ориентированные задачи, умения самостоятельно формулировать задачи профессионального и жизненного плана. Идея состоит в том, что использование данных задач способствует обеспечению более осознанного овладения математической теорией и практикой и в дальнейшем окажет влияние на более успешную социализацию выпускников в современном обществе. Список литературы http://festival.1september.ru/articles/625875/ http://ru.convdocs.org/docs/index-2161.html#28238 Алгебра: сборник заданий для подготовки к итоговой аттестации в 9 кл. [Текст]: Итоговая аттестация / Л.В. Кузнецова, С.Б. Суворова, Е.А. Бунимович, Л.О. Рослова.- М.: Просвещение, 2006.- 192 с. Алгебра [Текст]: Учеб. для 7 кл. общеобразоват. учреждений / С.М. Никольский, М.К. Потапов, Н.Н. Решетников и др.- 2-е изд.- М.: Просвещение, 2008.- 285 с. Алгебра [Текст]: Учеб. для 7 кл. общеобразоват. Учреждений / Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др.- 8-е изд.- М.: Просвещение, 2008.- 207 с. Алгебра [Текст]: Учеб. для 7 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков и др.; под ред. С.А. Теляковского.- 9-е изд.- М.: Просвещение, 2008.- 223 с. Алгебра [Текст]: Учеб. для 8 кл. общеобразоват. учреждений / С.М. Никольский, М.К. Потапов, Н.Н. Решетников и др.- М.: Просвещение, 2007.- 287 с. Алгебра [Текст]: Учеб. для 8 кл. общеобразоват. Учреждений / Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др.- 44-е изд.- М.: Просвещение: Моск. учеб.», 2008.- 255 с.: ил. Алгебра [Текст]: Учеб. для 8 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков и др.; под ред. С.А. Теляковского.- 3-е изд.- М.: Просвещение, 2006.- 239 с. Алгебра [Текст]: Учеб. для 9 кл. общеобразоват. учреждений / С.М. Никольский, М.К. Потапов, Н.Н. Решетников и др.- М.: Просвещение, 2008.- 255 с. Алгебра [Текст]: Учеб. Для 9 кл. общеобразоват. Учреждений / Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др.- 10-е изд.- М.: Просвещение: Моск. учеб., 2006.- 255 с. Алгебра [Текст]: Учеб. для 9 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков и др.; под ред. С.А. Теляковского.- 3-е изд.- М.: Просвещение, 2006.- 271 с. Печёнкина Е.Н. Практико-ориентированные задачи на уроках математики в основной школе // Электронный ресурс [http://rudocs.exdat.com/docs/index-100680.html] Колягин Ю.М. и Пикан В.В. О прикладной и практической направленности обучения математике : Математика в школе. 1985. © 6. http://nsportal.ru/shkola/algebra/library/prikladnaya-napravlennost-pri-obuchenii-matematike-0 Тесты по математике 5-11 кл. – М.: ООО «Агентство «КРПА «Олимп»: «Издательство АСТ»,2002. 425с. Рубинштейн С. Л. О мышлении и путях его исследования. – М.: Изд-вог Акад. наук СССР, 1958. – 147с. |
