материаловедение. Методические рекомендации по выполнению расчётнографического задания
 Скачать 0.65 Mb. Скачать 0.65 Mb.
|
|
Федеральное агентство по образованию Тверской государственный технический университет Кафедра Электроснабжения и электротехники материаловедениеКонтрольноЕ заданиЕ для студентов специальности Электроснабжение заочной формы обучения Тверь 2008 г. УДК 621.3 Методические указания содержат описание трёх расчётно-графических заданий по исследованию свойств электротехнических материалов. Составитель: к.т.н. В.В. Воропаев Воропаев В.В. Общие методические рекомендации по выполнению расчётно-графического задания 1. ЭЛЕКТРОПРОВОДНОСТЬ ДИЭЛЕКТРИКОВ Под действием постоянного напряжения через технический диэлектрик протекает ток утечки
где Iск и Iаб – соответственно сквозной и абсорбционный токи, А. Абсорбционные токи возникают в диэлектриках в результате поляризационных процессов смещения связанных зарядов. По окончании поляризации абсорбционный ток спадает до нуля, а ток утечки становится равным сквозному току (рис. 1). 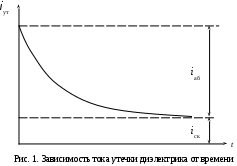 Сквозной ток возникает в диэлектриках за счёт наличия небольшого числа свободных ионов, электронов или коллоидных частиц. Для твёрдых диэлектриков как абсорбционный, так и сквозной токи имеют две составляющие. Так, например, для сквозного тока
где Если объёмный ток обусловлен наличием свободных зарядов в объёме диэлектрика, то поверхностный ток – наличием водорастворимых загрязнений и плёнки влаги на поверхности диэлектрика (рис. 3). Плотность объёмного тока в однородном и изотропном диэлектрике определяется из выражения
где V – удельная объёмная проводимость диэлектрика, См/м; V – удельное объёмное сопротивление диэлектрика, Омм; Е – напряжённость электрического поля, В/м. 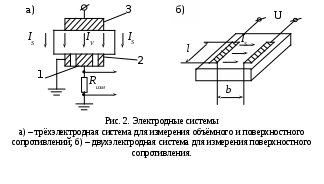 Объёмное и поверхностное сопротивления диэлектриков, как правило, весьма высоки, поэтому для их определения используются чувствительные гальванометры, электрометры и тераомметры, позволяющие измерять токи до 10-17 …10-15 А. На практике для раздельного измерения объёмного IV и поверхностного IS токов применяется, в соответствии с ГОСТ 6433.2-80, трёхэлектродная система (рис. 2, а). В случае плоского образца на обе его стороны наносятся напылённые или прижимные электроды. С одной стороны расположены кольцевой 2 и измерительный 1 электроды, с другой – дисковый электрод 3 (рис. 2, а). При измерении объёмного сопротивления потенциал измерительного электрода 1 оказывается чуть выше потенциала кольцевого электрода 2, поэтому поверхностный ток IS полностью отводится на кольцевой электрод. На измерительный электрод, таким образом, попадает только объёмный ток IV. Удельное объёмное сопротивление диэлектрика
где RV – объёмное сопротивление, Ом; S – площадь измерительного электрода, м2; t – толщина образца диэлектрика, м. 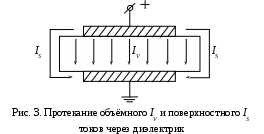 При измерении поверхностного сопротивления также применяется система из двух электродов, нанесённых на одну сторону плоского образца (рис. 2, б). Электроды имеют форму двух параллельных полос, расположенных на расстоянии b. Удельное поверхностное сопротивление
где l – длина электрода, м, b – расстояние между электродами, м. Если допустить, что приложенные к диэлектрику электроды обладают достаточно малым сопротивлением и диэлектрик является однородным, то без учёта поверхностной проводимости для тела любой формы и размеров можно ввести понятие приведённой длины . Приведённая длина диэлектрика имеет размерность длины и однозначно определяет соотношение параметров тела (электрической проводимости G, См, электрического сопротивления, R, Ом, и электрической ёмкости C, Ф) между электродами и характеристик материала. Так, электрическая проводимость тела равна
электрическое сопротивление
ёмкость
Для тела длиной h, м, и сечением S, м2, произвольной конфигурации, но постоянным по всей длине тела (например, проволока или жила кабеля, диэлектрик плоского конденсатора), электрическое сопротивление
следовательно, приведённая длина этого тела определятся по выражению
Весьма важен случай, когда тело имеет форму трубы, на внешнюю и внутреннюю стороны которой нанесены электроды (например, диэлектрик цилиндрического конденсатора, изоляция одножильного коаксиального кабеля). Обозначив осевую длину электрода через l, а внутренний и внешний радиусы трубы соответственно через r1 и r2, можем найти сопротивление между электродами, рассмотрев его как результирующее сопротивление последовательно соединенных сопротивлений dR бесконечно тонких слоёв, имеющих толщину dx и радиус х. Сопротивление такого слоя составляет:
Интегрируя в пределах от x = r1 до x = r2 , получаем сопротивление
Следовательно, в этом случае приведённая длина
2. ДИЭЛЕКТРИЧЕСКИЕ ПОТЕРИ В диэлектрике, помещённом в электрическое поле, происходит процесс поляризации. Явление поляризации диэлектрика вызывается смещением электрических зарядов на ограниченные расстояния под действием сил внешнего и внутреннего электрических полей. Поляризация бывает безынерционная (электронная, ионная), не сопровождающаяся потерями энергии, и инерционная (релаксационная), вызванная такими перемещениями электронов, ионов и дипольных молекул, которые сопровождаются значительными потерями энергии в диэлектрике. На переменном напряжении с угловой частотой ток I через конденсатор с идеальным диэлектриком (т.е. без потерь) опережает по фазе напряжение U на угол 90. Наличие диэлектрических потерь в конденсаторе с реальным диэлектриком приводит к тому, что ток I опережает напряжение U на угол < 90 (рис. 4). б) а) 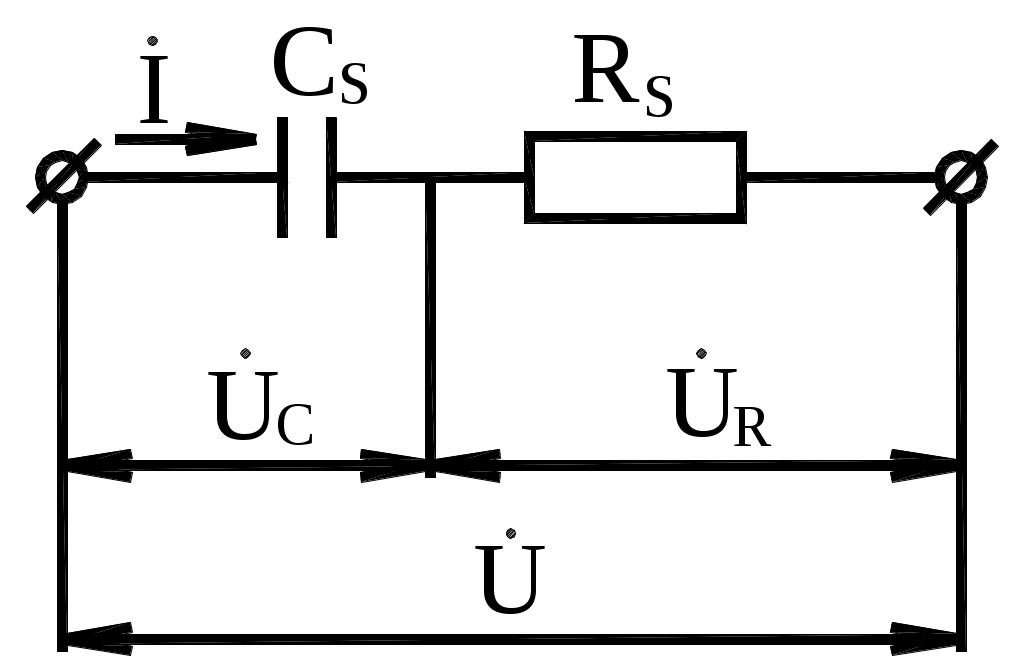 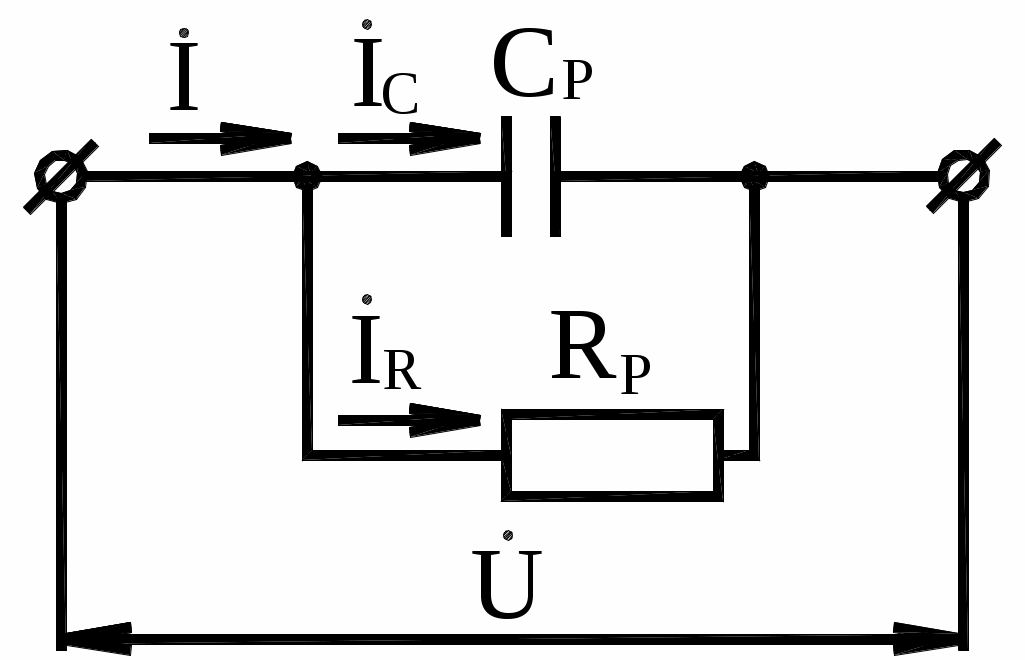 в) г) 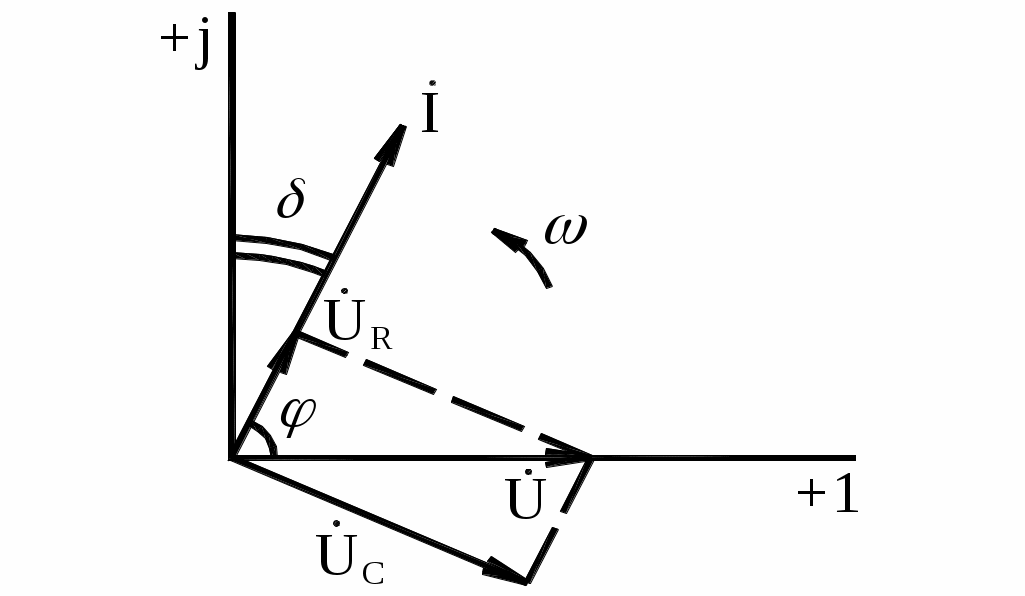 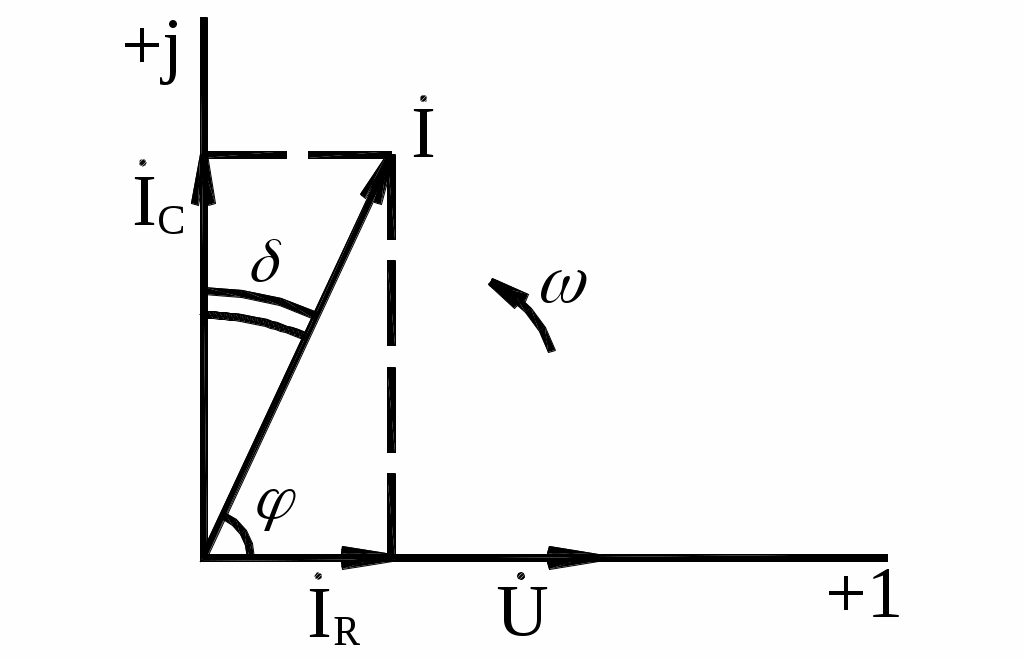 Рис. 4. Последовательная и параллельная схемы замещения диэлектрика с потерями и их векторные диаграммы Угол , дополняющий угол сдвига фаз между током и напряжением до 90, называется углом диэлектрических потерь. Рассмотрим наиболее распространённые эквивалентные схемы замещения диэлектрика с потерями: последовательную (рис. 4, а) и параллельную (рис. 4, б). В последовательной схеме замещения сумма активной UR и реактивной UC составляющих напряжения даёт приложенное напряжение U. Здесь
а мощность диэлектрических потерь
В параллельной схеме замещения сумма активной IR и реактивной IC составляющих тока даёт ток через диэлектрик I. Здесь
а мощность диэлектрических потерь
Поскольку CpCsC,а tg<< 1, то для обеих схем замещения
Если потери в конденсаторе с диэлектриком обусловлены главным образом сопротивлением подводящих проводов с сопротивлением самих электродов, то для анализа используется последовательная схема замещения. В этом случае диэлектрические потери
возрастают пропорционально квадрату частоты. Если потери в диэлектрике обусловлены высокой сквозной проводимостью, то используют параллельную схему замещения. В этом случае диэлектрические потери
не зависят от частоты. 3. Электрическая прочность Пробой диэлектриков происходит в сильных электрических полях и связан с образованием проводящего канала в диэлектрике. Напряжённость поля, при которой диэлектрик теряет свои электроизоляционные свойства, называется пробивной напряжённостью, или электрической прочностью Епр. Различают пробой в однородном и неоднородном поле. Приблизительно однородное поле обеспечивается для сферических электродов, если радиус сферы много больше длины зарядного промежутка (толщины диэлектрика). В случае однородного электрического поля электрическая прочность диэлектрика рассчитывается по формуле
где Unp – пробивное напряжение, d – толщина диэлектрика. В условиях эксплуатации важно знать, какое напряжение способно выдержать то или иное электрическое изделие. Напряжение, приложенное к электрической изоляции изделия, должно быть значительно ниже той величины, при которой наступает электрический пробой. Минимальное напряжение, при котором происходит пробой, называется пробивным напряжением Unp. Основной же характеристикой материала служит пробивная напряжённость (или электрическая прочность) Епр, определяемая из соотношения (3.1). Величина электрической прочности характеризует качество диэлектрика и зависит от его свойств. Однако Епр значительно зависит от условий испытания, от толщины диэлектрика, рода тока, скорости подъёма напряжения, формы электродов, температуры и атмосферного давления и т.д. Для того чтобы при испытаниях получались воспроизводимые величины Епр для каждого материала, необходимо проводить опыты с соблюдением ряда требований, которые регламентируются ГОСТ 6433.3-80. На электрическую прочность изоляционных материалов значительное влияние оказывает их неоднородность. Неоднородность диэлектрика вызывает искажение электрического поля, в котором расположен данный диэлектрик. Предположим сначала, что макроскопически неоднородный диэлектрик находится в переменном электрическом поле и что проводимостью и диэлектрическими потерями его можно пренебречь, то есть = и tg = 0. При этих допущениях единственным параметром диэлектрического материала, который может оказывать влияние на распределение напряжённости электрического поля по его объёму, является диэлектрическая проницаемость r. При макроскопически однородном по всему объёму диэлектрике напряжённость электрического поля в каждой точке диэлектрика вообще не зависит от r диэлектрического материала. Так, в случае плоского конденсатора напряжённость поля определяется (3.2) для всех точек диэлектрика между обкладками, и поле является равномерным.
где U – напряжение между обкладками, В; d – толщина диэлектрика, м. Цилиндрический конденсатор даёт нам простейший пример неравномерного электрического поля. Согласно (3.3) максимальная напряжённость имеет место в точках, расположенных в непосредственной близости от внутренней обкладки (при х = r1), а минимальная – в непосредственной близости от внешней (при х = r2).
где U – напряжение между обкладками, В; r1 и r2 – соответственно радиусы внутренней и внешней обкладок, м; x – расстояние от оси цилиндрического конденсатора, м. В плоском конденсаторе, содержащем два (или более) различных диэлектрика, соединенных параллельно, поле равномерно, и его напряжённость также определяется формулой (3.2). Рассмотрим теперь конденсатор с различными диэлектрическими материалами, слои которых соединены последовательно друг с другом (слоистый диэлектрик). Напряжённость поля в каждом из последовательно соединенных слоёв уже неодинакова. Она будет обратно пропорциональна диэлектрической проницаемости материала данного слоя. Электрическое смещение D в плоском конденсаторе постоянно во всем объёме диэлектрика; обозначая для двухслойного плоского конденсатора Е1 и E2 – напряжённости в слоях 1 и 2 и r1 и r2 – относительные диэлектрические проницаемости материала этих слоев, имеем
Рассчитаем значения напряжённости поля в слоях двухслойного плоского конденсатора. Обозначим h1 и h2 – толщины слоёв и U1 и U2 – напряжения на них, получим при последовательном соединении слоёв
где U – полное напряжение на конденсаторе, В. Решение системы уравнений (3.4) и (3.5) даёт значения напряжённости поля в обоих слоях
В общем случае плоского многослойного (m слоёв) конденсатора
Для многослойного цилиндрического конденсатора (общий случай m слоёв) напряжённость на расстоянии x от оси (в j-м слое)
|

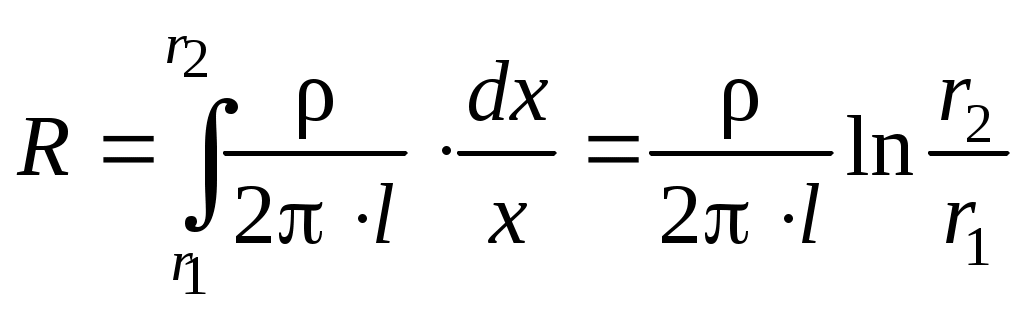
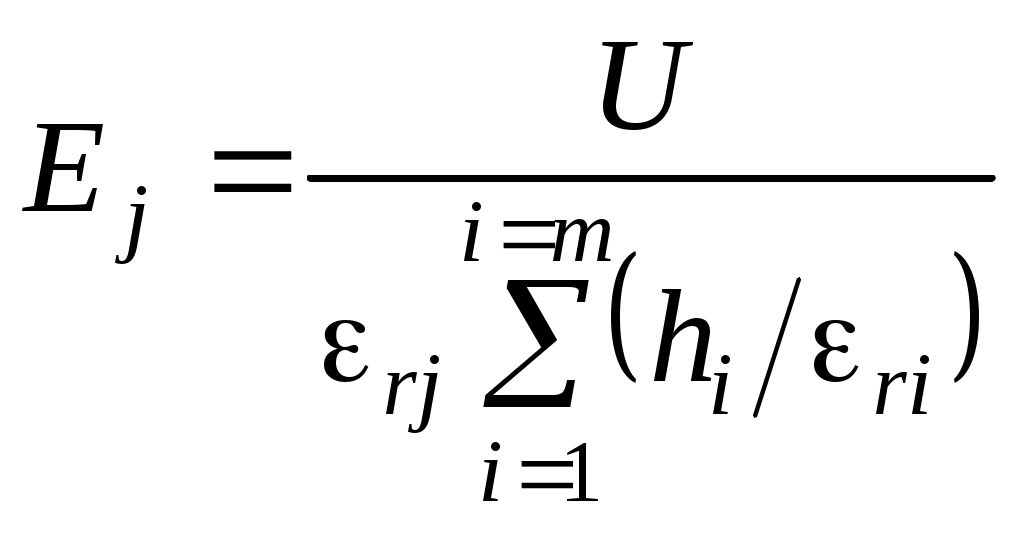 .
.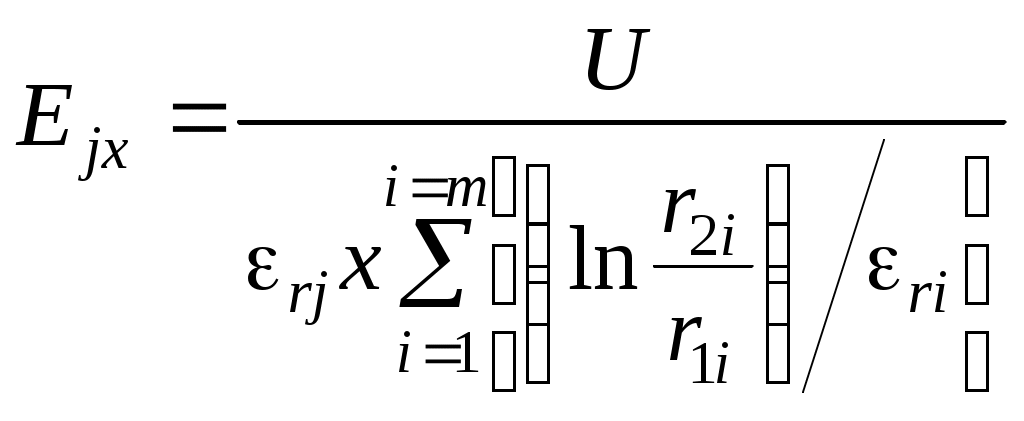 .
.