№ п/п
|
Основные
понятия
|
Содержание
|
1
|
Статистическое наблюдение
|
Первая стадия всякого статистического исследования, представляющая собой научно организованный по единой программе учет фактов, характеризующих явления и процессы общественной жизни, и сбор полученных на основе этого учета массовых данных
|
2
|
Генеральная совокупность
|
Совокупность наблюдаемых данных при сплошном наблюдении, т.е. всех единиц изучаемой совокупности
|
3
|
Выборочная совокупность
|
Совокупность единиц, выбранных из генеральной совокупности
|
4
|
Ошибка выборки
|
Разность между показателями генеральной и выборочной совокупностями
|
5
|
Группировка
|
Разбиение совокупности на группы, однородные по какому-либо признаку
|
6
|
Интервал
|
Количественная граница группы, разность между верхней и нижней границами
|
7
|
Вариационный ряд
|
Ряд распределения, построенный по количественному признаку
|
8
|
Ряд распределения
|
Группировка, в которой для характеристики групп применяется один показатель – численность группы
|
9
|
Формула Стерджесса
|
Число групп вариационного ряда n=1+3,322 lg N, где N – число элементов совокупности
|
10
|
Статистическая таблица
|
Средство наглядного и рационального представления результатов статистического исследования в виде граф и строк
|
11
|
Статистический график
|
Условное изображение числовых величин и их соотношений в виде различных геометрических образов – точек, линий, плоских фигур и т.п.
|
12
|
Полигон
|
Геометрическая фигура – ломаная линия, соединяющая вершины, абсциссами которых являются значения варьирующегося признака, а ординатами – соответствующие им частоты
|
13
|
Гистограмма
|
Геометрическое изображение интервального вариационного ряда, где на оси абсцисс откладываются границы интервалов, являющиеся основаниями прямоугольников, площади которых равны либо пропорциональны частотам
|
14
|
Кумулята
|
Ломаная линия, вершины которой имеют в качестве абсцисс – значение признака (или граница интервала), ординаты – нарастающие итоги частот
|
15
|
Степенная средняя невзвешенная
(простая)
|
x1, x2,…,xn – варианты 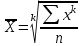
|
16
|
Степенная средняя взвешенная
|
f1,f2,…,fn – вес или частота 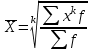
|
17
|
Средняя
гармоническая
|
Невзвешенная (простая) взвешенная
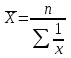 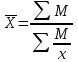 , где М – объем явления, М=xf , где М – объем явления, М=xf
|
18
|
Средняя
арифметическая
|
Невзвешенная (простая) 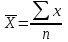
Взвешенная 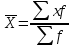
|
19
|
Средняя
геометрическая
|
Невзвешенная 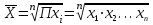
|
20
|
Средняя
квадратическая
|
Невзвешенная (простая) 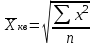
Взвешенная 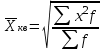
|
21
|
Правило
мажорантности средних
|
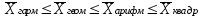
|
22
|
Мода
|
Наиболее часто встречающееся значение признака для интервального ряда:
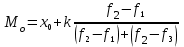
|
23
|
Медиана
|
Величина признака, которая делит упорядоченную последовательность его значений на две равные по численности части
Для интервального ряда:
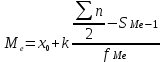
|
24
|
Квартили
|
Значение признака, делящее ранжированную совокупность на четыре равновеликие части для интервального ряда:
нижний квартиль
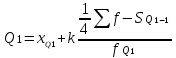
верхний квартиль
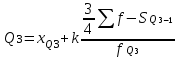
|
25
|
Децили
|
Значение признака, делящее ранжированную совокупность на десять равновеликих частей
|
26
|
Вариационный размах
|
R=Xmax-Xmin – разница между максимальным и минимальным значениями признака
|
27
|
Среднее линейное отклонение
|
Невзвешенная Взвешенная
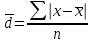 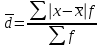
|
28
|
Дисперсия
|
Невзвешенная 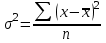
Взвешенная 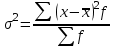
Упрощенный способ (моментов) 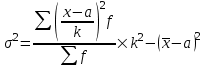
|
29
|
Среднее
квадратическое
отклонение
|
Невзвешенная 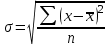
Взвешенная 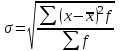
|
30
|
Коэффициент
осцилляции
|
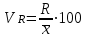
|
31
|
Относительное
линейное
отклонение
|
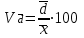
|
32
|
Коэффициент
вариации
|
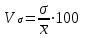
|
33
|
Правило сложения дисперсий
|
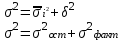
|
34
|
Дисперсия
альтернативного признака
|
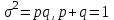
|
35
|
Эмпирический
коэффициент
детерминации
|
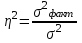
|
36
|
Эмпирическое
корреляционное отношение
|
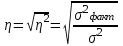
|
37
|
Средняя ошибка выборки
при случайном
повторном отборе
|
Генеральная совокупность:
для средней для доли
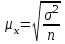 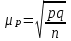
Выборочная совокупность:
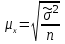 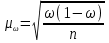
|
38
|
Предельная ошибка при случайном
повторном отборе
|
Для средней Для доли
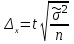 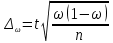
|
39
|
Предельная ошибка при механическом (бесповторном)
отборе
|
Для средней Для доли
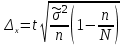 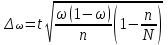
|
40
|
Необходимый
объем выборки
при случайном
повторном отборе
|
Для средней Для доли
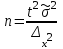 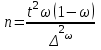
|
41
|
Необходимый
объем выборки
при случайном
бесповторном
(механическом)
отборе
|
Для средней Для доли
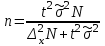 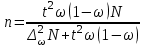
|
42
|
Ряд динамики
|
Последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления
|
43
|
Абсолютные
приросты в рядах динамики
|
Для ряда динамики y0, y1,…yn абсолютный прирост:
базисный Δбаз =yi – y0; цепной Δцепн =yi - yi-1
|
44
|
Темп роста в рядах динамики
|
Для ряда динамики y0, y1,…yn
базисный Тр= 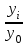 ; цепной Тр= ; цепной Тр= 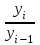
|
45
|
Темп прироста в рядах динамики
|
базисный Тпр= 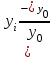 ; цепной Тпр= ; цепной Тпр= 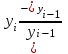
|
46
|
Средний
абсолютный
прирост
|
Для ряда динамики y0, y1,…yn
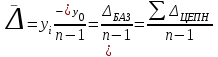
|
47
|
Средний темп роста
|
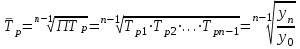
|
48
|
Коэффициент
опережения
|
По темпам роста и прироста показывает, во сколько раз один темп роста больше другого
|
49
|
Метод наименьших квадратов
|
Метод выявления зависимости изменения ряда динамики путем обеспечения наименьшей суммы квадратов отклонений фактических уровней от выравненных
|
50
|
Тренд
|
Тенденция динамики, как правило выраженная в форме уравнения, наилучшим образом аппроксимирующего фактическую тенденцию динамики
|
51
|
Параметры
линейного тренда
|
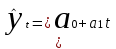 ; a0, a1 – параметры прямой, t – показатель времени. Система нормальных уравнений ; a0, a1 – параметры прямой, t – показатель времени. Система нормальных уравнений
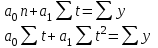 при при 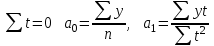
|
52
|
Индекс сезонности в стабильных рядах
|
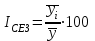 , , 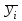 -осредненные эмпирические данные по одноименным периодам; -осредненные эмпирические данные по одноименным периодам; 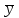 - общая средняя - общая средняя
|
53
|
Индекс сезонности с тенденцией роста
|
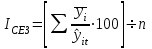 где где 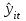 - переменная средняя (выравненные уровни) - переменная средняя (выравненные уровни)
|
54
|
Вероятностные границы интервала прогнозируемого явления
|
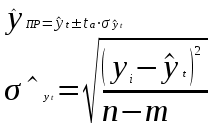 где n – число уровней ряда динамики, m – число параметров адекватной модели тренда где n – число уровней ряда динамики, m – число параметров адекватной модели тренда
|
55
|
Индивидуальный индекс
|
Относительная величина, характеризующая соотношение уровней по отдельному виду единиц совокупности
|
56
|
Общий индекс стоимости товара
|
В случае неоднородности изучаемого явления сравнение уровней происходит после приведения их к одной общей мере, например, индекс общего объема товарооборота (индекс стоимости) в фактических ценах имеет вид: 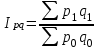
|
57
|
Агрегатный индекс цен
|
Пааше 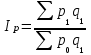 - объем выпуска в текущем периоде; - объем выпуска в текущем периоде;
Ласпейреса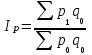 – объем выпуска в базисном периоде – объем выпуска в базисном периоде
|
58
|
Агрегатный индекс объема
|
Пааше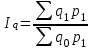 – цены текущего периода – цены текущего периода
Ласпейреса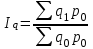 – цены базисного периода – цены базисного периода
|
59
|
Средний индекс цен
|
Пааше 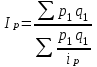 Ласпейреса Ласпейреса 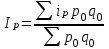
|
60
|
Средний индекс объема
|
Пааше 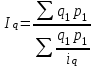 Ласпейреса Ласпейреса 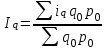
|
61
|
Индекс средней цены или индекс переменного состава
|
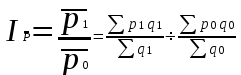
|
62
|
Индекс постоянного состава
|
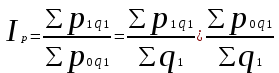
|
63
|
Индекс
структурных
сдвигов
|
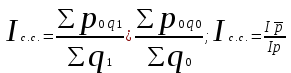
|
64
|
Регрессионный анализ
|
Выбор типа модели (формы связи), установление степени влияния независимых переменных на зависимую и определение расчетных значений зависимой переменной (функции регрессии)
|
65
|
Корреляционный анализ
|
Измерение тесноты известной связи между варьирующими признаками, определение неизвестных причинных связей и оценок факторов, оказывающих наибольшее влияние на результативный признак
|
66
|
Прямолинейная
однофакторная связь
|
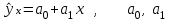 - параметры - параметры
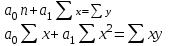
|
67
|
Индекс корреляции
|
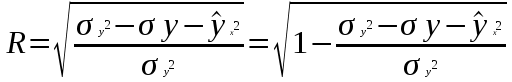 , где , где
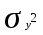 - общая дисперсия - общая дисперсия 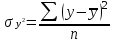 , ,
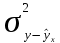 - остаточная дисперсия - остаточная дисперсия 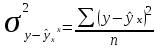
|
68
|
Линейный коэффициент корреляции
|
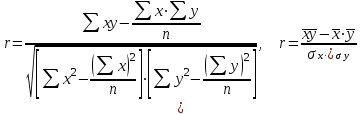
|
69
|
Коэффициент регрессии (через коэффициент корреляции)
|
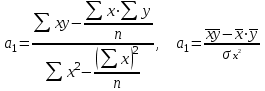
|
70
|
Коэффициент эластичности по фактическим данным
|
абсолютный 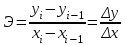
относительный 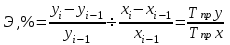
|
71
|
Коэффициент эластичности по выравненным данным
|
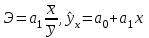 средний коэффициент эластичности средний коэффициент эластичности
|
 Скачать 411.37 Kb.
Скачать 411.37 Kb.