Контрольная. Методические рекомендации Введение в процессе изучения дисциплины Статистика и эконометрика
 Скачать 411.37 Kb. Скачать 411.37 Kb.
|
|
Методические рекомендации Введение В процессе изучения дисциплины «Статистика и эконометрика» каждый бакалавр выполняет контрольную работу, выполнение которой обеспечивает системную, последовательную работу студентов над курсом в течение всего времени его изучения по учебному плану. Контрольная работа носит комплексный характер и охватывает основные методы статистического анализа; с абсолютными, относительными и средними величинами; методы статистического изучения связи между социально-экономическими явлениями; методы работы с макроэкономическими показателями в системе национального счетоводства. Контрольная работа является самостоятельной работой бакалавров, отражающей уровень усвоения теоретического материала и глубину практических знаний, полученных бакалаврами в процессе обучения. Основная задача контрольной работы по модулю статистики – постановка, исследование и определение путей решения актуальных проблем, связанных с теорией и практикой статистики. При выполнении контрольной работы необходимо руководствоваться следующими требованиями: Работа может быть выполнена машинописным текстом. Типовая структура контрольной работы включает следующие разделы: Титульный лист (только машинописный текст) Рецензия на контрольную работу (должна быть вложена, не скреплять) Оглавление (с указанием страниц). Решение заданий (каждое задание переписывается и решается с новой страницы). Вывод к каждой задаче обязателен. Список использованной литературы (только за последние 5 лет, допускаются ссылки на электронные страницы). Работа должна быть представлена в срок (установленный планом ИНДО). Работа должна выполняться в той последовательности, которая установлена в содержании задания. Решение следует сопровождать необходимыми формулами, указав, что означают символы в них. Решение следует по возможности оформлять в виде таблиц. В конце каждого результата четко формулировать выводы. Все расчеты относительных показателей нужно производить с принятой в статистике точностью до 0,001, а проценты - до 0,1. Таблицы следует оформлять в соответствии с правилами, принятыми в статистике. При удовлетворительном выполнении работа оценивается и допускается к защите. Если студент не может самостоятельно выполнить контрольную работу или какую-то ее часть, следует обратиться к преподавателю в часы консультаций. Задания к контрольной работе составлены в десяти вариантах. Выбор варианта зависит от начальной буквы фамилии студента.
Работа включает два раздела статистики: I раздел – «Теория статистики»: задания 1, 2, 3, 4, 5, 6, 9(реферативная часть) и II раздел – «Социально-экономическая статистика»: задания 7, 8.Самовольная замена одного варианта задания другим не разрешается. Приступая к выполнению контрольной работы, необходимо ознакомиться с соответствующими разделами программы курса и методическими указаниями, изучить литературу. Особое внимание нужно обратить на технику расчета и экономический смысл статистических показателей. Студенты, предоставившие на проверку неудовлетворительные работы, выполняют работу или заново, или вносят исправления в соответствии с замечаниями рецензента. Студенты, не получившие зачета по предусмотренным учебным планом письменным работам, к экзамену не допускаются. Оценивание результатов самостоятельной деятельности бакалавров по решению задач производится в соответствии с «Положением об академическом рейтинге студентов». Максимальный результат, который может быть достигнут бакалавром по каждому заданию или упражнению – 100 %. Если студент получает рейтинговую оценку ниже 100 %, то значит какая-то часть материала им не освоена и не нашла отражение в представленном им решении задания или упражнения. Введение рейтингового механизма оценивания не отменяет существующую зачетную шкалу, перевод в которую студент осуществляет самостоятельно, пользуясь следующим соотношением: 0– 50 % – «не зачтено», «неудовлетворительно»; 51 – 100 % – «зачтено». Результирующей оценкой по всем задачам или упражнениям выполненным студентом по заданию преподавателя является средняя оценка, также выраженная в баллах, например:
Тогда результирующую оценку определяем как отношение суммы всех оценок к их количеству 599 : 8 = 74,9 % - «хорошо» или «зачтено». Рейтинговая система оценки работы студентов является единой для всех учебных направлений и профилей в УрГЭУ. Вариант 10 В 2015 г. среднегодовая численность населения города составила 2036.6 тыс. чел., в 2014 г. 2051.6 тыс. чел., в 2013 г. 2061.2 тыс. чел. Определите цепные относительные величины динамики (с точность до 0,1;%) в % Найти значение медианы для ряда распределения:
Каким должен быть коэффициент вариации, чтобы совокупность была однородной и почему? Опрос общественного мнения по знакомству с устройством КПК, показал что из 786 опрошенных респондентов 283 не слышали о данном устройстве. Оценить в процентах доверительный интервал людей в генеральной совокупности не знакомых с данным устройством при вероятности 0,954 Цены на бензин в 4 квартале текущего года по сравнению с 4 кварталом предыдущего года возросли за 1 литр с 23 до 27 рублей. Каков ежеквартальный темп прироста цен на бензин (в %) Определить недостающие числа в формуле для расчета индекса влияния структурных сдвигов на изменения урожайности средней урожайности зерновых культур (индекс структурных сдвигов) и рассчитать его при условии: 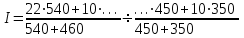
Сделать выводы. Имеются данные о выработке продукции работниками предприятия за два периода:
Чему равен индекс выработанной продукции в %? Индекс средней дневной продолжительности труда рабочих равен 0,98; индекс средней фактической продолжительности рабочего дня – 1,2. Найти индекс средней часовой производительности труда. 9.Реферат на тему : Исследование социально-экономических явлений с помощью многофакторных моделей индексов. .(за последние 5 лет) ЦЕЛЬ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ ПО МОДУЛЮ ЭКОНОМЕТРИКА Контрольная работа выполняется студентами заочного отделения, изучающими дисциплину “Статистика и эконометрика” раздел Эконометрика с целью более глубокого ознакомления с содержанием тем курса; овладения возможностями анализа информации; развития у студентов способностей к оцениванию конкретной социально-экономической ситуации, постановке задачи и выбору методов ее решения; укрепления навыков формулирования выводов о состоянии и развитии изучаемого явления или процесса, построения прогнозов. Решение контрольной работы призвано выполнить следующие учебные задачи: – закрепление знаний, умений, полученных на лекционных и практических занятиях; – освоение навыков выполнения базовых этапов эконометрического исследования: построение эконометрических моделей, оценка параметров построенной модели; проверка качества найденных параметров модели и самой модели в целом; верификация модели; – использование построенных моделей для объяснения поведения исследуемых экономических показателей и построение прогнозов развития экономической ситуации. 2. ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ Задания контрольной работы выполняются студентами по вариантам Решения и анализ задач оформляется на листах MS Excel в произвольной форме в соответствие с вопросами, перечисленными в условии. Решения должны содержать таблицы и графики и пояснения к ним. 3. СОДЕРЖАНИЕ КОНТРОЛЬНОЙ РАБОТЫ Контрольная работа предполагает решение задачи. Таблица исходных статистических данных генерируются каждому студенту индивидуально в программной среде MS Excel с использованием генератора случайных чисел. Пример условия задачи, решения, анализа и справочный материал приведены в приложении. 4. УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ Основная литература Бородич, С. А. Эконометрика. Практикум : Учебное пособие / С. А. Бородич. – Нальчик : ООО "Научно-издательский центр ИНФРА-М", 2015. – 329 с. http://znanium.com/go.php?id=502332 Кочкина, Е. М. Эконометрика : учебное пособие [для студентов экономических специальностей всех форм обучения...] / Е. М. Кочкина, Е. В. Радковская ; М-во образования и науки Рос. Федерации, Урал. гос. экон. ун-т. - Екатеринбург : [Издательство УрГЭУ], 2013. – 176 с. http://lib.usue.ru/resource/limit/ump/13/p478725.pdf Тимофеев В.С., Фаддеенков А.В., Щеколдин В.Ю. Эконометрика: учебник для бакалавров. – 2-е изд., перераб. и доп. – М.: Юрайт, 2013. – 328 с. Эконометрика: учебник для вузов / под ред. В.Б. Уткина. – 2-е изд. – М.: Дашков и К, 2013. – 561с. Новиков А.И. Эконометрика: учебное пособие. – М.: Дашков и К, 2013. – 224с. Эконометрика: учеб. для студентов вузов по специальности 080601 «Статистика» и др. междисциплинар. специальностям / И.И. Елисеева [и др.]; под ред. И.И. Елисеевой. – М.: Проспект, 2009. – 288 с. Эконометрика : учебник для магистров : учебник для студентов вузов, обучающихся по экономическим направлениям и специальностям / [И. И. Елисеева [и др.]; под ред. И. И. Елисеевой ; С.-Петерб. гос. экон. ун-т. – Москва : Юрайт, 2014. – 449 с. Доугерти К. Введение в эконометрику : учеб. для студентов экон. специальностей вузов / пер. с англ.: [О. О. Замков и др., науч. ред. пер. О. О. Замков]. – 2-е изд. – М. : ИНФРА-М, 2004. – 419 с. Дополнительная литература Гладилин А.В., Гарасимов А.Н., Громов Е.И. Эконометрика : учеб. пособие для студентов вузов – М.: Кнорус, 2011. – 227 с. Кремер Н.Ш., Путко Б.А. Эконометрика : учеб. для студентов вузов, обучающихся по специальностям экономики и упр. / под ред. Н.Ш. Кремера. – 2-е изд., стер. – М.: ЮНИТИ, 2008. – 311 с. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс : Учеб. для студентов вузов, обучающихся по экон. специальностям / Акад. нар. хоз-ва при Правительстве Рос. Федерации. – 6-е изд., перераб. и доп. – М.: Дело, 2004. – 575 с. Магнус Я.Р., Катышев П.К,. Пересецкий А.А. Сборник задач к начальному курсу эконометрики : учеб. пособие / Акад. нар. хоз-ва при правительстве Рос. Федерации. – М.: Дело, 2002. – 207 с. Замков О.О. Эконометрические методы в макроэкономическом анализе: Курс лекций. – М.: ГУ ВШЭ, 2001. – 122 с. Приложение Пример решения задачи контрольной работы Условие. Менеджер новой чебуречной не уверен в правильности выбранной цены на чебуреки, поэтому на протяжении 17 периодов он варьирует цену и отслеживает количество проданных чебуреков. Статистические данные приведены в таблице. Ставятся следующие задачи: 1) построить эконометрическую модель зависимости количества проданных чебуреков от цены; 2) исследовать качественные характеристики построенной эконометрической модели; 3) на основе модели определить оптимальную в смысле максимума выручки цену чебурека. В таблице1 представлены собранные менеджером статистические данные, занесенные в электронную таблицу Microsoft Excel. 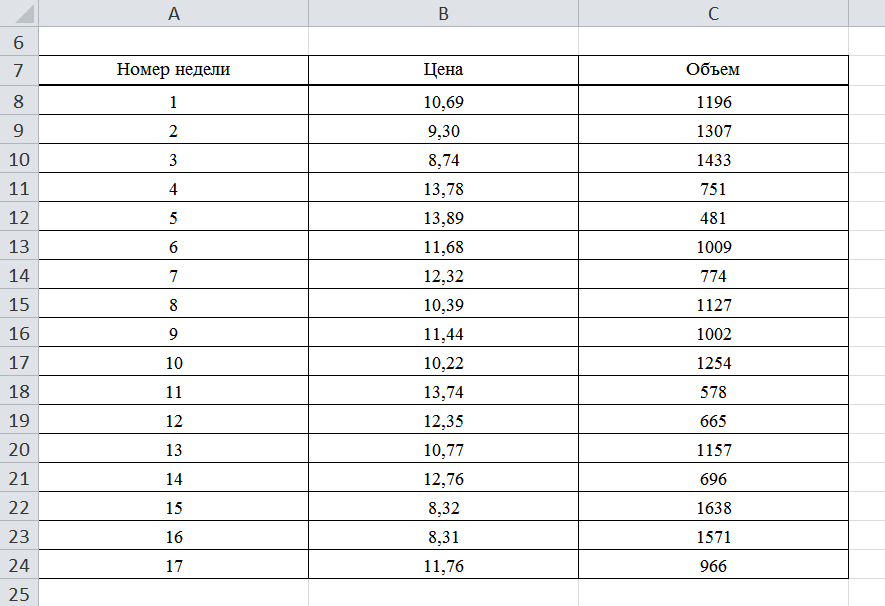 Табл.1. Таблица исходных данных для построения модели Для получения численного решения задачи в Microsoft Excel следует воспользоваться программой анализа данных стандартного Пакета анализа. В версиях Excel 2007 и выше для выполнения регрессионного анализа необходимо выполнить команду: Данные → Анализ данных→Регрессия. При отсутствии опции Анализ данных в меню Данные Пакет анализа следует подгрузить с помощью опции Надстройки. В результате на экран вызывается окно диалога, которое необходимо заполнить: Входной интервал Y: выделяются все значения зависимой переменной вместе с названием (в нашем случае, объем), т.е. выделяются ячейки, в которых содержатся числовые значения объема (в нашем случае, С7:С24); Входной интервал Х: выделяются все значения независимой переменной вместе с названием (в нашем случае, цена) , т.е. выделяются ячейки, в которых содержатся числовые значения цены (в нашем случае, В7:В24); В позиции Метки ставится флажок, т.к. во входные интервалы включены не только числовые значения, но и имена переменных; Помимо диапазона входных данных, задается информация о параметрах вывода. Результаты регрессионного анализа могут быть выведены на текущий рабочий лист, на отдельный рабочий лист (установкой флажка возле опции Новый рабочий лист), в новый файл (установкой флажка возле опции Новая рабочая книга) или на текущий рабочий лист (установкой флажка возле опции Выходной интервал). В последнем случае результаты решения будут выведены на тот же лист, где находятся исходные данные задачи, начиная с той позиции, которая будет указана пользователем в поле Выходной интервал. В нашем случае в параметрах вывода в позиции Выходной интервал указывается адрес ячейки, являющейся левой верхней ячейкой диапазона вывода результатов (ячейка А30); В позициях Остатки и Стандартизованные остатки ставятся флажки, поскольку эти результаты необходимы для полноценного анализа. В 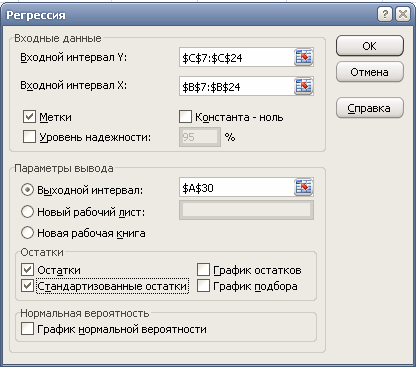 ид окна диалога в нашем случае представлен на рис. 1. Рис. 1. Окно диалога «Регрессия» После заполнения всех необходимых полей диалога и нажатия кнопки «ОК» на экран будет выведено решение задачи (рис.2). 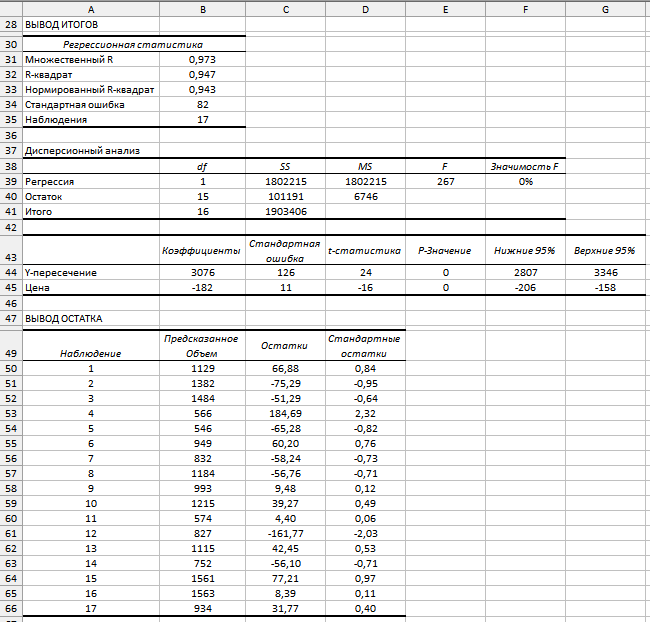 Рис. 22. Результаты решения задачи в пакете Excel Результаты проведенного регрессионного анализа выводятся в четырех таблицах под общим названием Вывод итогов. Для полноценного анализа полученных результатов необходимо решить четыре выше описанные задачи регрессионного анализа. Определение числовых значений коэффициентов модели. Регрессионная модель в общем случае имеет вид: у = a + b x. В нашей задаче объем продаж выполняет роль зависимой переменной у, а цена одного чебурека является факторной переменной х. Для записи регрессионной модели в частном (а не общем) виде необходимо определить числовые значения параметров а и b. Числовые значения параметров а и bвыведены в столбце Коэффициенты третьей таблицы Вывода итогов. Здесь Y-пересечение является константой уравнения регрессии (параметр а). В нашем случае константа а равна 3076. Формально параметр а определяет величину y при нулевом значении х. Т.е. условно можно сказать, что при нулевой цене чебурека объем их продаж составит 3076 штук. Однако поскольку в реальности цена не может иметь нулевого значения, то буквальная трактовка параметра а не имеет экономического смысла. Коэффициент регрессии b показывает величину изменения результата при увеличении фактора на единицу. В случае, когда b < 0, связь между показателями является обратной, т.е. с ростом х снижается y. В нашем случае b равно –182, следовательно, с ростом цены на 1 р. объем продаж снижается в среднем на 182 чебурека. Выполнив анализ коэффициентов, можно записать полученную регрессионную модель: Объем = 3075 – 182 ЦЦена. Коэффициент регрессии b дает возможность оценить, как в среднем меняется результирующий показатель при изменении фактора. Но поскольку в эконометрических исследованиях редко имеется возможность использовать генеральную совокупность данных, необходимо проанализировать границы изменения найденных коэффициентов. Для этого рассмотрим доверительные интервалы коэффициентов, выведенные в столбцах Нижние 95% и Верхние 95%. Доверительный интервал показывает интервал изменения соответствующего параметра регрессии в 95% случаев при тех или иных изменениях исходных данных. В нашем примере величина константы при изменении исходных данных почти наверняка (с вероятностью 95%) будет лежать в интервале от 2807 до 3346, а величина коэффициента перед переменной Цена – в интервале от –206 до –158. Т.о., в среднем при росте цены на 1 р., объем продаж снижается на 182 чебурека. В лучшем случае объем продаж снизится на 158 чебуреков при увеличении цены на 1 р. В худшем случае объем продаж снизится на 206 чебуреков при увеличении цены на 1 р. Анализ статистической значимости коэффициентов регрессионной модели. Помимо коэффициентов регрессии в третьей таблице Вывода итогов в столбце Стандартная ошибка выведены значения стандартных отклонений коэффициентов модели для генеральной совокупности. В нашем случае стандартная ошибка коэффициента а равна 126, а коэффициента b равна 11. Для обоих коэффициентов значения стандартных ошибок не превышают половины модуля величины коэффициента (3076 и –182 соответственно), поэтому можно сделать вывод о том, что данные коэффициенты являются достоверными. Далее проверяется вероятность выполнения нулевой гипотезы для найденных коэффициентов a и b с использованием статистики Стьюдента, числовые значения которой приводятся в столбце t-статистика. Для нашего примера статистика Стьюдента для параметра а составляет 24, для параметра b равна –16. На основании этих значений рассчитываются вероятности выполнения нулевых гипотез для обоих параметров, которые выводятся в столбце Р-Значение. В нашем случае вероятность выполнения нулевой гипотезы для коэффициента а (т.е. вероятность того, что а = 0) равна нулю (меньше порогового значения в 5%). Т.о., можно считать параметр а отличным от нуля и статистически достоверным. Вероятность выполнения нулевой гипотезы для коэффициента b (т.е. вероятность того, что b = 0) также равна нулю. Т.о., параметр b тоже можно считать отличным от нуля и статистически достоверным. Обобщая вышесказанное, подчеркнем, что Р-Значение определяет: вероятность выполнения нулевой гипотезы для соответствующего коэффициента регрессии; т.е. вероятность незначимости (недостоверности) соответствующего коэффициента регрессии; т.е. вероятность того, что фактор x не оказывает линейного влияния на результативный показатель y. Расчет и анализ показателей качества построенной регрессионной модели. Расчет показателей качества модели проводится на основе таблицы Дисперсионный анализ (вторая таблица Вывода итогов). В столбце SS указаны значения дисперсий: объясняемой регрессионной моделью (RSS), остаточной (ESS) и общей (TSS). TSS – это сумма квадратов отклонений реальных значений у от среднего значения у. Величина TSS выводится в строке Итого. В нашем случае величина TSS равна 1 903 406. RSS – это сумма квадратов отклонений модельных значений у от среднего значения у. Величина RSS выводится в строке Регрессия. В нашем случае величина RSS равна 1 802 215. ESS – это сумма квадратов отклонений реальных значений у от модельных значений у. Величина ESS выводится в строке Остаток. В нашем случае величина ESS равна 101 191. Зная значение дисперсий, можно рассчитать один из показателей качества регрессионной модели – коэффициент детерминации. Числовое значение коэффициента детерминации выводится в первой таблице Вывода итогов в строке R-квадрат. R-квадрат – коэффициент детерминации, рассчитывается как отношение объясненной дисперсии (RSS) к общей дисперсии (TSS). В нашем случае 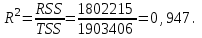 R-квадрат определяет: долю дисперсии, объясненную регрессионной моделью; долю разброса данных, объясненного регрессионной моделью; долю наблюдений, попавших под описание регрессионной модели. У нас доля объясненной дисперсии составляет 94,7%, т.е. под описание регрессионной модели попадает 94,7% наблюдений. Наряду с коэффициентом детерминации, в первой таблице Вывода итогов выводится величина уточненного коэффициента детерминации Rнорм – в строке Нормированный R-квадрат. Для расчета уточненного коэффициента детерминации используются значения степеней свободы, которые выводятся во второй таблице в столбце df. Общее число степеней свободы выводится в строке Итого и рассчитывается как количество наблюдений минус один (n–1). Число степеней свободы для величины RSS выводится в строке Регрессия и рассчитывается как разность между количеством наблюдений и числом факторных переменных (n–k). Число степеней свободы для величины ESS выводится в строке Остаток и рассчитывается как разность между количеством наблюдений и количеством переменных модели (n–k–1). В нашем случае значения степеней свободы равны соответственно 16, 15 и 1. Объясненная и остаточная дисперсии на одну степень свободы выводятся в столбце MS второй таблицы Вывода итогов. Для расчета общей дисперсии на одну степень свободы следует разделить величину общей дисперсии на соответствующее количество степеней свободы, равное (n–1). В нашем случае объясненная дисперсия на одну степень свободы равна 1 802 215, остаточная дисперсия на одну степень свободы равна 6 746, общая дисперсия на одну степень свободы равна 118 963. Чтобы рассчитать уточненный коэффициент детерминации необходимо из единицы вычесть отношение остаточной дисперсии на одну степень свободы к общей дисперсии на одну степень свободы. В результате для нашего примера получаем величину Rнорм = 0,943, которая выводится в первой таблице в строке Нормированный R-квадрат. Нормированный R-квадрат определяет долю дисперсии (т.е. долю разброса данных), объясненную факторами модели. Вычислив квадратный корень из коэффициента детерминации, получаем коэффициент корреляции, который измеряет тесноту связи в регрессионной модели и выводится в строке Множественный R первой таблицы Вывода итогов. Коэффициент корреляции является важнейшим показателем для оценки качества регрессионной модели. Этот показатель определяет, насколько тесно связаны между собой зависимая и факторная переменные в построенной модели. Значение коэффициента корреляции близко к единице (Множественный R = 0,973), что свидетельствует о наличии достаточно тесной связи между исследуемыми экономическими показателями и подтверждает влияние цены чебурека на изменение объема продаж. В некоторых случаях низкое значение коэффициента корреляции может быть связано с наличием в изучаемой выборке аномальных наблюдений – статистических выбросов, которые искажают как величины коэффициентов регрессии, определяющих меру влияния фактора на результат, так и характеристику тесноты связи. Если величина коэффициента корреляции в решаемой задаче меньше 0,7, то, в первую очередь, следует проверить наличие статистических выбросов. Если объем статистической выборки позволяет ее сократить, то даже при приемлемом значении коэффициента корреляции рекомендуется исключать из набора исходных данных статистические выбросы. Статистический выброс – это наблюдение, резко отклонившееся от линии регрессии вверх или вниз. Если наблюдение является статистическим выбросом, его стандартный остаток по абсолютной величине больше или равен 2. Величины стандартных остатков выводятся в столбце Стандартные остатки четвертой таблицы Вывода итогов. В нашем случае 4-е и 12-е наблюдения являются статистическими выбросами. С определенной долей условности можно считать, что для остальных наблюдений реальный и модельный объем продаж приблизительно совпадают. 4-е наблюдение является выбросом вверх (стандартный остаток = 2,32). Это не означает, что объем продаж в 4-м периоде был слишком большим. Появление этого выброса связано с тем, что при установленной в 4-м периоде цене объем продаж был значительно выше, чем можно было бы ожидать согласно построенной модели. 12-е наблюдение является выбросом вниз (стандартный остаток = –2,03). Это также не означает, что объем продаж в 12-м периоде был мал. Появление этого выброса связано с тем, что при установленной в 12-м периоде цене объем продаж был существенно ниже, чем можно было бы ожидать согласно построенной модели. В нашем случае исходный объем выборки составлял 17 наблюдений, что позволяет удалить два обнаруженных выброса. Процедура удаления статистических выбросов заключается в удалении из исходных данных тех строк, которые соответствуют наблюдениям-выбросам (в нашем случае это 11 и 19 строки). Для измененных данных повторяется процедура регрессионного анализа, результаты проведения которого представлены на рис. 3. 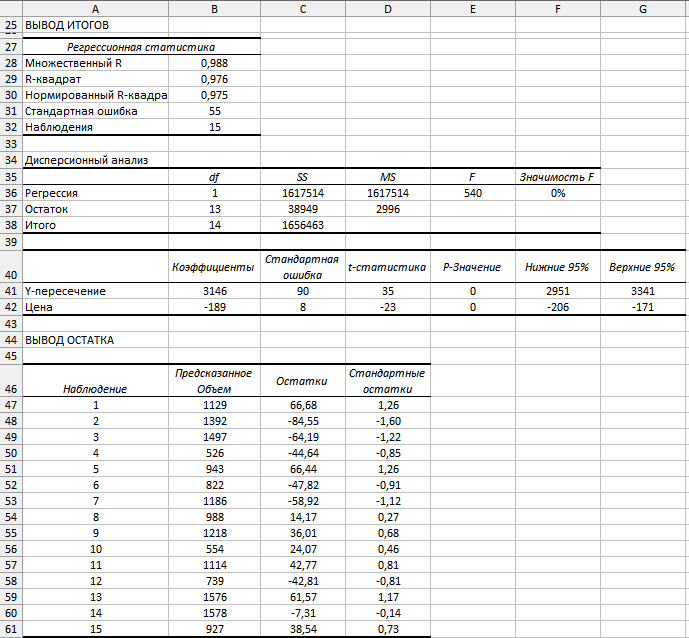 Рис. 3. Результаты решения задачи после удаления выбросов в пакете Excel Как видно из рис. 3, удаление статистических выбросов позволило повысить тесноту связи между ценой и объемом продаж. Коэффициент корреляции, измеряющий тесноту связи, увеличился с 0,973 до 0,988. Соответственно, увеличилась и доля объясненного разброса данных до 97,6%. Отметим, что изменилась и мера влияния цены на объем продаж, а именно: увеличение цены на 1 р. приводит к снижению объема продаж на 189 чебуреков. Последнее значение следует признать более точным. В результате удаления статистических выбросов изменились и границы доверительных интервалов, они стали более узкими. Подчеркнем, что чем уже доверительный интервал, тем точнее полученные результаты. По величине остатков можно сравнить фактические и теоретические значения зависимой переменной. Если остаток для какого-либо наблюдения больше нуля, то реальное значение в этом наблюдении больше ожидаемого, и наоборот: при отрицательном остатке ожидаемое значение больше. Например, для рассматриваемой задачи в 6-м наблюдении фактическое значение объема продаж меньше ожидаемого, т.к. остаток для этого наблюдения равен –47,82. В 10-м наблюдении реальное значение объема продаж больше ожидаемого на 24,07, т.к. остаток для этого наблюдения равен 24,07. В четвертой таблице Вывода итогов, помимо остатков и стандартных остатков, выводятся ожидаемые (по уравнению) значения зависимой переменной для каждого наблюдения. Для расчета ожидаемых значений в построенной регрессионной модели фактор х должен последовательно принять все реальные значения из изучаемой выборки. Модельные значения зависимой переменной у выводятся в столбце Предсказанное у. Для решаемой задачи столбец имеет название Предсказанное Объем и содержит теоретические значения объема продаж для всех 15-ти наблюдений. Например, в 14-м наблюдении теоретический объем продаж равен 1578. Это значение можно получить подстановкой в регрессионную модель значения цены для 14-го периода: Объем = 3146 – 189· ЦЦена = 3146 – 189· 8,31 = 1578. Определение статистической достоверности построенной регрессионной модели. Статистическая достоверность регрессионной модели проверяется с помощью нулевой гипотезы для коэффициента детерминации. Величина статистики Фишера выведена во второй таблице Вывода итогов в столбце F. В нашем случае величина F равна 540. С помощью статистики Фишера определяется вероятность выполнения нуль-гипотезы для коэффициента детерминации, которая выводится в столбце Значимость F. В нашей задаче Значимость F равна нулю, следовательно, нулевая гипотеза отвергается на 95%-м уровне значимости, а коэффициент детерминации признается статистически достоверным. Значимость F определяет: вероятность выполнения нулевой гипотезы для коэффициента детерминации R2; т.е. вероятность того, что наблюдений для проведения регрессии недостаточно. После выполнения регрессионного анализа делается общий вывод о качестве построенной модели. Особое внимание при оценке качества необходимо уделить следующим аспектам анализа: связь между изучаемыми показателями должна быть тесной, т.е. коэффициент корреляции (Множественный R) должен быть больше или равен 0,7; коэффициенты модели, определяющие меру влияния факторов на результат, должны быть достоверными, т.е. все Р-Значения должны быть меньше 5%; регрессионная модель в целом должна быть достоверна (количество наблюдений должно быть достаточным), т.е. величина Значимость F должна быть меньше 5%; (необязательное условие) результаты регрессионного анализа не должны содержать статистических выбросов, которые могут быть удалены. Задача нахождения оптимальной цены чебурека, при которой достигается максимум выручки. Выручку можно рассматривать как произведение цены на объем продаж. Для простоты введем обозначения: V – объем продаж, Р – цена одного чебурека. Уравнение регрессии в таком случае записывается в следующем виде: V = 3146 – 189 P. Если обе части данного уравнения умножить на Р, то левая часть будет содержать формулу выручки, и можно записать: VР = 3146· P – 189· P2. Из курса математического анализа известно, что для нахождения экстремума функции необходимо ее производную приравнять к нулю. Возьмем производную по цене от выручки и приравняем ее к нулю: (V· P)'p = 3146 – 189· P = 0. Из последнего равенства легко найти оптимальное значение цены. 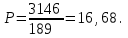 Если взять вторую производную от выручки по цене и проанализировать знак полученного результата, то можно убедиться в том, что в данной точке действительно достигается максимум функции, т.к. вторая производная отрицательна: (V· P) ''p = –189. Т.о., для достижения максимальной выручки менеджеру следует установить цену продажи одного чебурека на уровне 16,68 р. Глоссарий и формулы | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
