реферат. Методические указания Абакан 2011

• Название: Методические указания Абакан 2011
• Анкор: реферат
• Дата: 24.11.2022
• Размер: 0.86 Mb.
• Имя файла: Tekhnicheskaya_termodinamika_i_teploobmen_Dokument_Microsoft_Wor.doc
• Тип: Методические указания; #810407
• страница: 4 из 5

Задача 9

1. 
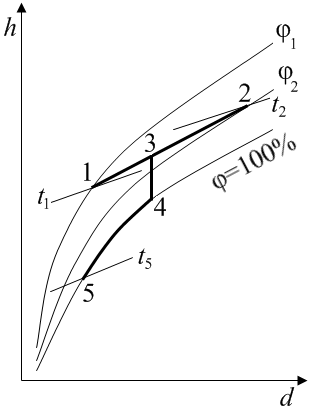
   Дать понятия теплопроводности, теплоотдачи и теплопередачи.
   
2. 
   Охарактеризовать стационарный режим теплообмена.
   
3. 
   Перечислить факторы, определяющие величину термического сопротивления твердой стенки. Указать пути его снижения.
   

Задача 10

1. 
   Дать понятие мощности внутренних источников теплоты q_v, Вт/м³.
   
2. 
   Графически изобразить характер распределения температуры в теле с внутренними источниками теплоты, окруженном жидкостью.
   

Задача 11

1. 
   Дать понятие коэффициента температуропроводности вещества, выразить его через другие физические параметры.
   
2. 
   Написать выражения критериев подобия Био и Фурье для неограниченной пластины и цилиндра бесконечной длинны, а также безразмерной температуры. Подставить размерности физических величин в выражения критериев и убедиться, что критерии безразмерны.
   
3. 
   Указать последовательность определения нестационарного температурного поля одномерного тела.
   
4. 
   Сформулировать теорему перемножения решений.
   

Задача 12

1. 
   Охарактеризовать ламинарный, переходный, турбулентный режимы движения жидкости.
   
2. 
   Написать выражения основных критериев подобия, используемых в расчетах конвективного теплообмена: Рейнольдса, Нуссельта, Прандтля, Грасгофа. Пояснить входящие в выражения физические величины, дать их размерности.
   
3. 
   Указать последовательности определения коэффициента теплоотдачи при конвективном теплообмене с помощью критериального уравнения.
   

Задача 13

1. 
   Охарактеризовать природу лучистого теплообмена.
   
2. 
   Сформулировать закон Стефана-Больцмана, написать его аналитическое выражение.
   
3. 
   Дать понятие степени черноты тела.
   
4. 
   Написать выражение приведенного коэффициента излучения для системы двух тел, одно из которых находиться в полости другого.
   

Задача 14

1. 
   Объяснить устройство и работу кожухотрубного теплообменного аппарата.
   
2. 
   Изобразить графики изменения температуры теплоносителей вдоль теплообменной поверхности рекуперативного теплообменника применительно к прямоточной и противоточной схемам их движения. Показать на графиках большую и меньшую разности температур Δt_б, Δt_м.
   

3. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ
Задача 1
Чтобы представить давление кислорода в различных единицах измерения, можно воспользоваться следующей зависимостью:

1 бар=10⁵ Па=0,987атм.физ.=1,02 атм.техн.=750 мм рт.ст.=10,2 м вод. ст.

Температура кислорода может быть выражена в Кельвинах Т, К, градусах Реомюра t_R, °R, градусах Фаренгейта t_F, °F, градусах Ренкина t_Ra, °Ra, исходя из заданной температуры в градусах Цельсия t, °C, с помощью известных соотношений:
; ; ; .
Удельный объем реального газа при относительно низком давлении и высокой температуре находят по уравнению Клапейрона.
Задача 2
Кажущаяся молярная масса газовой смеси µ, кг/кмоль, может быть выражена через объемные доли и молярные массы компонентов:
,
где – объемная доля i-го компонента; – молярная масса i-го компонента, кг/кмоль.

Газовая постоянная смеси R, Дж/(кг·К), равна отношению универсальной газовой постоянной к кажущейся молярной массе:
.
Объем газовой смеси V, м³, может быть найден из уравнения Клапейрона:

,

где – давление смеси, Па; M – масса смеси, кг; T – температура смеси, К.

Парциальный объем V_i, м³ , парциальное давление p_i, Па, массовую долю m_i и массу М_i, кг, каждого компонента находят по формулам:
; ; ; .
Изобарная массовая теплоемкость газовой смеси, с_p может быть вычислена как сумма произведений теплоемкостей компонентов с_pi, Дж/(кг·К), на их массовые доли m_i:
.
Теплота, подводимая к газу при изобарном нагреве, Дж,

Изохорную теплоемкость с_v, Дж/(кг·К), определяют их уравнения Майера:
.
Теплота, подводимая к газу при изохорном нагреве, Дж:
.

Задача 3
Молярную массу азота , его газовую постоянную R, изобарную и изохорную теплоемкости с_p и с_v, показатель адиабаты k определяют по справочнику или находят из соотношений:
, , .
Теплоемкость политропного процесса c_n, кДж/(кг·К), выражается через изохорную теплоемкость, показатель адиабаты и показатель политропы:


Недостающие основные параметры состояния газа p, ν, T в характерных точках могут быть последовательно вычислены с применением уравнения Клапейрона и известных зависимостей между параметрами состояния в адиабатном и политропном процессах:
;
Изменения внутренней энергии Δu и энтальпии Δh идеального газа в любом термодинамическом процессе выражаются формулами, кДж/кг:
; ,
где, ΔT – изменение температуры, K.

Изменение энтропии в изотермическом, изобарном и политропном процессах, кДж/(кг·К):
; ; .
Теплота, отводимая в изотермическом, изобарном и политропном процессах, кДж/кг:
; ;
Работа сжатия l, кДж/кг, в каждом рассматриваемом процессе может быть определена из уравнения первого закона термодинамики по известным отводимой теплоте и изменению внутренней энергии газа.
Задача 4
Задача может быть решена с применением h,d-диаграммы влажного воздуха. По заданным параметрам t₁, φ₁ и t₂, φ₂ на диаграмме строят точки 1 и 2, соответствующие исходным состояниям воздуха (рис.2).

Точка 3, отражающая свойства воздуха, получившегося в результате смешения двух порций, находиться на отрезке прямой 1-2. Расстояния от точки 3 до концов отрезка пропорциональны массам порций:

	Для точки 3 определяют значения искомых параметров: t, h, φ, d, Pп, tp, tм. Процесс охлаждения ненасыщенного воздуха протекает при неизменном влагосодержании, следовательно, изображается на диаграмме вертикальной линей 3-4. Дальнейшее охлаждение после достижения состояния насыщения сопровождается удалением из воздуха части воды в форме конденсата и снижением его влагосодержания (отрезок 4-5). Положение конечной точки 5 определяется пересечением линий φ=100% и изотермы t5.
Рис. 2. Изображение процессов смешения и охлаждения воздуха на h,d - диаграмме

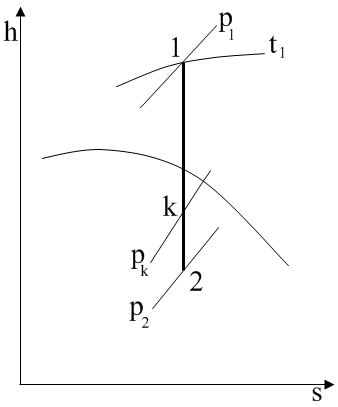
Поскольку охлаждение происходит при постоянном давлении, то отведенная теплота q, кДж/(кг сух. возд.), рассчитывается как разность энтальпий воздуха в начале и конце процесса:
.
Масса образовавшегося конденсата m, г/(кг сух. возд.), равна разности влагосодержаний в точках 4 и 5.
.
Задача 5
Задачу удобно решать c применением h,s-диаграммы водяного пара. Теоретический процесс адиабатного истечения изображается на диаграмме отрезком вертикальной прямой 1-2 (рис.3).

Точка 1 соответствует состоянию пара в котле и строится по известным параметрам P₁ и t₁. Точка 2 характеризует пар, поступающей в атмосферу, находится на пересечении изоэнтропы, опущенной из точки 1, и изобары, соответствующей атмосферному давлению P₂=0,1 МПа.

Для определения скорости истечения пара необходимо вычислить критическое давление P_k, МПа:

На пересечении линий 1-2 и изобары P_k наносят точку k.

При P_k>P₂ скорость истечения через цилиндрический патрубок равна критической ω_k, м/с, массовый расход пара будет максимальным М_max, кг/с.

Расчеты производят по формулам: , , где h1, hk – удельные энтальпии пара в точках 1 и k, Дж/кг; vk – удельный объем пара в точке k. Скорость пара на выходе из сопла Лаваля ω2, м/с, выражается формулой:
	Рис. 3. График процесса изоэнтропного истечения пара

,
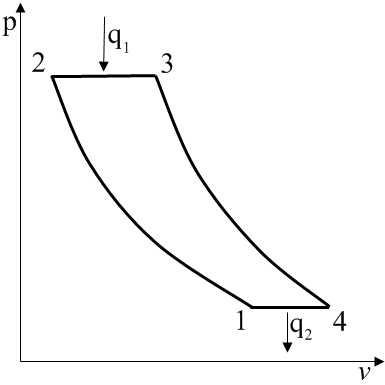
где h₂ – удельная энтальпия пара на выходе из сопла в точке 2, Дж/кг.

Расход пара через сопло Лаваля Может быть найден по уравнению неразрывности потока и параметрами минимального сечения канала.
Задача 6
Идеальный цикл ДВС с подводом теплоты при постоянном давлении – цикл Дизеля показан на рис. 4.

Степень сжатия равна отношению удельных объемов рабочего тела в точках 1 и 2 цикла .

Удельный объем до сжатия может быть найден из уравнения состояния идеального газа по известным температуре и давлению воздуха, поступающего в цилиндр.
,
где R = 287 Дж/(кг · К) – газовая постоянная воздуха.

Минимальная степень сжатия в дизельном двигателе должна быть такой, чтобы температура воздуха в конце сжатия достигла температуры воспламенения топлива t₂ = t_вос. Минимальная степень сжатия может быть найдена из соотношения, справедливого для адиабатного процесса:
,
где k – показатель адиабаты рабочего тела.

Действительная степень сжатия по условию задачи превышает минимальную на 20%, то есть .

Удельный объем рабочего тела в точке 2 цикла соответственно равен .

В точке 4 цикла, отражающей начало изохорного процесса 4-1, удельный объем газа совпадает с исходным удельным объемом v₄=v₁. В процессе 2-3 неизменным остается давление p₂ = p₃.

Чтобы определить недостающие основные параметры состояния газа в характерных точках цикла, нужно воспользоваться уравнениями адиабаты и , уравнением Клапейрона , выражением теплоподвода . Степень предварительного расширения рабочего тела в цикле: .
	Рис.4. Цикл ДВС с подводом теплоты при p=const: 1-2 – адиабатное сжатие, 2-3 – изобарный процесс с теплоподводом q1, 3-4 – адиабатное расширение, 4-1 – изохорный процесс с теплоотводом q2.

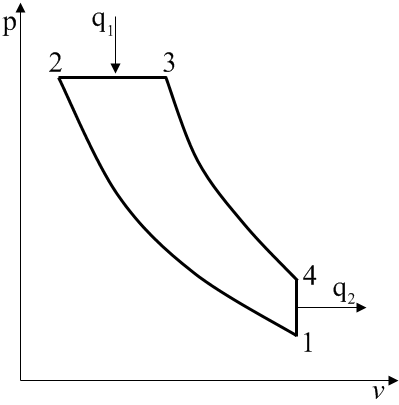
Термический КПД цикла Дизеля:
.
Полезная работа цикла:
.
Задача 7
На рис. 5 показан идеальный цикл газотурбинной установки с подводом теплоты при постоянном давлении – цикл Брайтона.

Степень повышения давления в компрессоре β представляет собой отношение давлений в точках цикла 2 и 1, следовательно, нетрудно найти давление в камере сгорания Р₂=βР₁.

Процессы 2-3 и 4-1 изобарные, то есть Р₂=Р₃, Р₄=Р_1.

Чтобы определить недостающие основные параметры состояния рабочего тела в характерных точках цикла, можно воспользоваться уравнением Клапейрона pv=RT, а также известными соотношениями параметров состояния газа в адиабатных процессах: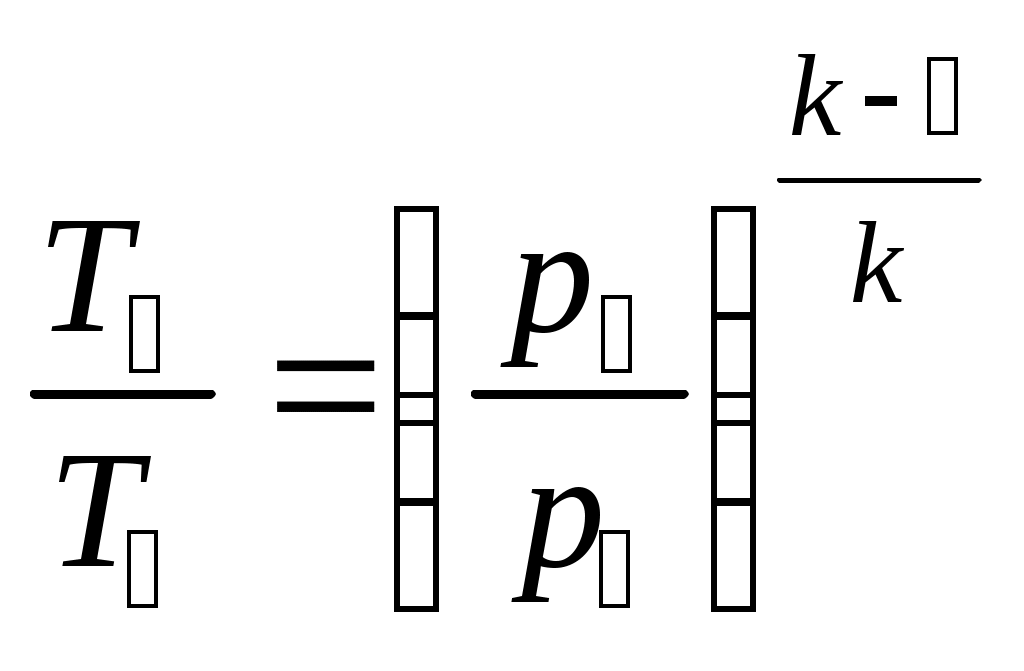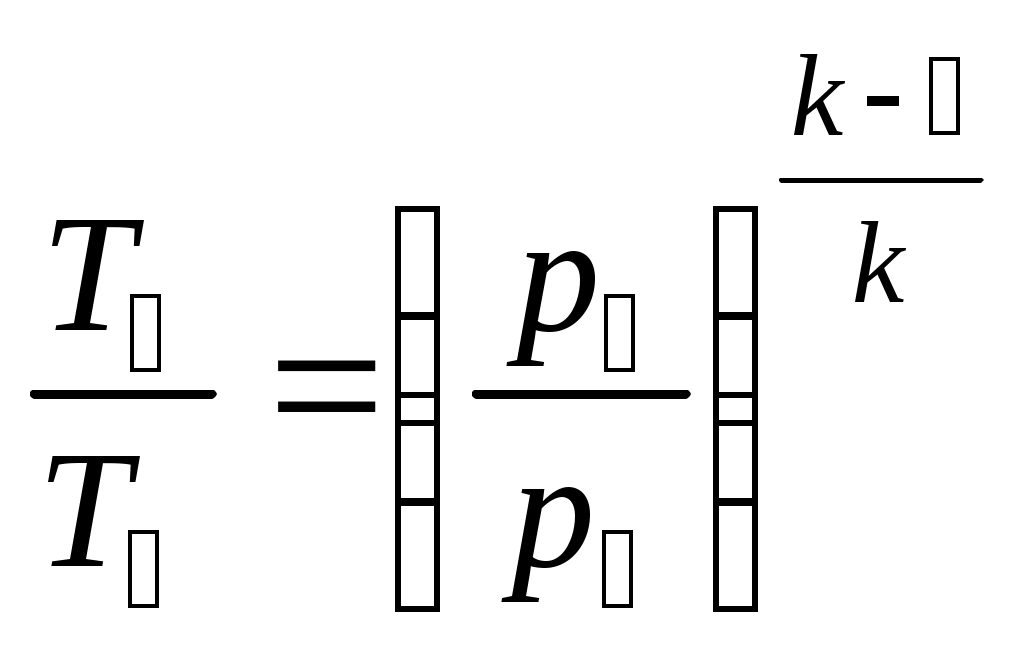
; .

	Подводимую и отводимую в цикле теплоту, полезную работу, термический КПД вычисляют по формулам: ; ; ; . Если газотурбинная установка имеет регенеративный подогреватель, и теплота от выхлопных газов передается воздуху, поступающему в камеру сгорания, то количество передаваемой таким образом теплоты выражается формулой, Дж/кг: ,
Рис. 5. Цикл ГТУ: 1-2 – адиабатное сжатие воздуха в компрессоре; 2-3 – изобарный процесс в камере сгорания; 3-4 – адиабатное расширение рабочего тела в турбине; 4-1 – изобарный выхлоп

где – удельная изобарная теплоемкость газов, Дж/(кг∙К); T₄, T₅ – температуры газов на входе в регенеративный подогреватель и выходе из него, К.

В этом случае необходимый теплоподвод к рабочему телу в камере сгорания и теплоотвод в окружающую среду одновременно снизятся на Δq. Термический КПД цикла может быть рассчитан по формуле: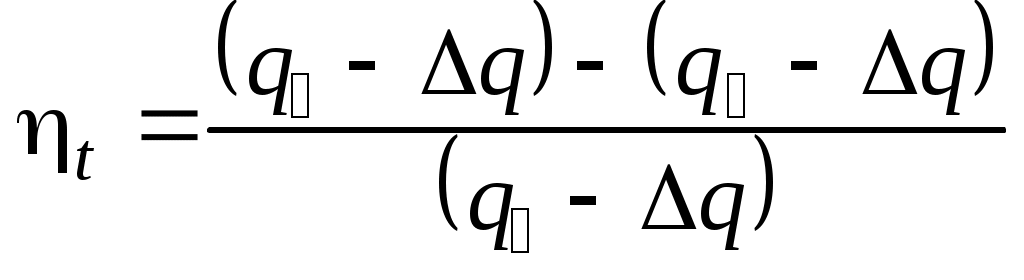
.