Дифференциальное исчисление функций одной действительной перемен. Методические указания к решению задач СанктПетербург Издательство спбгэту лэти 2009 удк 517. 22 (077)
 Скачать 1.04 Mb. Скачать 1.04 Mb.
|
|
Федеральное агентство по образованию ___________________________________ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» _______________________________________ Методы решения задач: техника вычисления производных. Методические указания к решению задач Санкт-Петербург Издательство СПбГЭТУ «ЛЭТИ» 2009 УДК 517.22 (077) Методы решения задач: техника вычисления производных: Методические указания к решению задач / Сост.: М. Н. Абрамова, К. Г. Межевич, Е. А. Толкачева. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2008. 32 с. Содержат определения, формулировки основных теорем и примеры решения задач различными методами по теме «Производная функции». Предназначены для студентов-заочников всех специальностей. Утверждено редакционно-издательским советом университета в качестве методических указаний © СПбГЭТУ «ЛЭТИ», 2009 Настоящее издание призвано помочь студентам-заочникам младших курсов самостоятельно научиться решать задачи по теме «Производная функции». Освоение этого раздела математического анализа на первый взгляд не вызывает затруднения у студентов. Но без четкого овладения именно техникой дифференцирования и понятием производной практически невозможно дальнейшее продвижение в освоении курса математического анализа. Поэтому первая часть методических указаний посвящена подробному обсуждению понятия «производная функции» и основных правил дифференцирования. Во второй части указаний рассматривается применения производной к решению ряда наиболее часто встречающихся задач. Данные методические указания, хоть и содержат теоретический материал, не призваны служить полной заменой учебника по теме «Производная функции», поэтому составители рекомендуют параллельно работать с учебным пособием «Конспект лекций по высшей математике» Д. Т. Письменного [1]. 1.ПРОИЗВОДНАЯ ФУНКЦИИ1.4.Понятие производной, ее геометрический и физический смысл.П 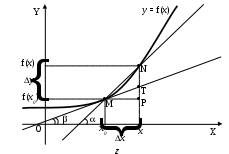 усть функция усть функция Из прямоугольного треугольника MPN Определение: Производной функции 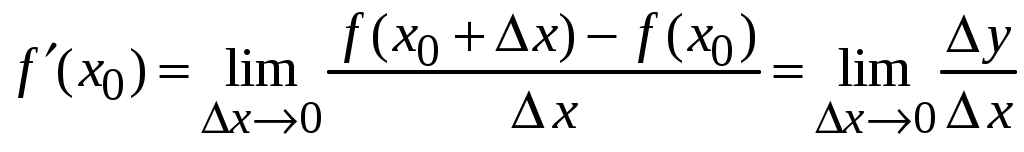 . .Геометрический смысл производной. Из рассуждений, приведенных выше видно, что производная функции Физический смысл производной. Если Быстрота протекания физических, химических и других процессов выражается с помощью производной. Сила и импульс по второму закону Ньютона связаны соотношением: Количество заряда, прошедшего через поперечное сечение проводника, определяет силу тока: В электростатическом поле, изменяющемся только по оси OX, напряженность и потенциал связаны соотношением: Если отношение 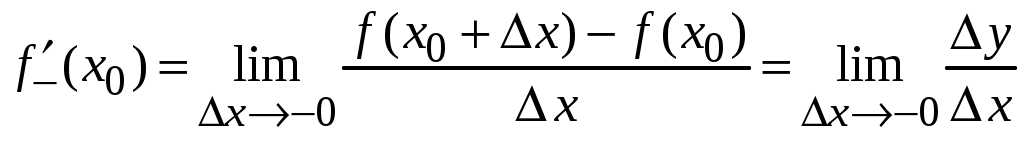 – производная слева; – производная слева;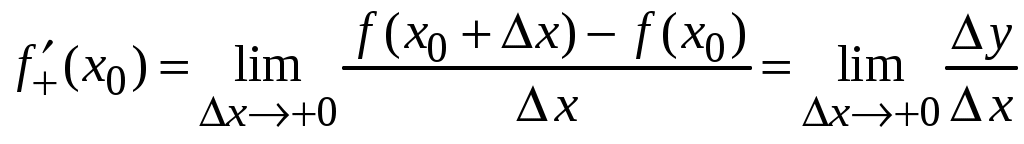 – производная справа. – производная справа.Очевидно функция, определенная в некоторой окрестности точки Если для некоторого значения x выполняется одно из условий 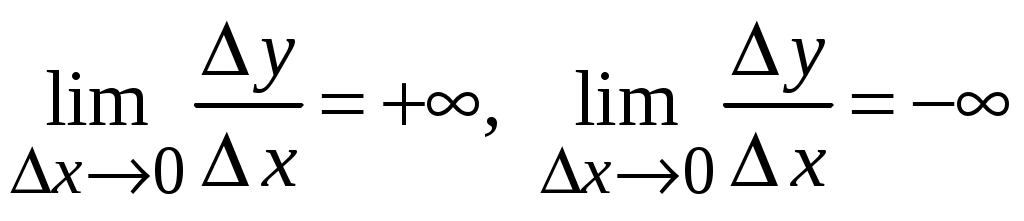 , то говорят, что в точке x существует бесконечная производная, равная соответственно , то говорят, что в точке x существует бесконечная производная, равная соответственно Функция, имеющая производную в данной точке, называется дифференцируемой в этой точке. Функция, имеющая производную в каждой точке данного промежутка, называется дифференцируемой в этом промежутке. Операция нахождения производной называется дифференцированием. Пример ПРОИЗВОДНАЯ ФУНКЦИИ.1. Пользуясь определением производной найти производную функции Решение: Зададим аргументу данной функции приращение 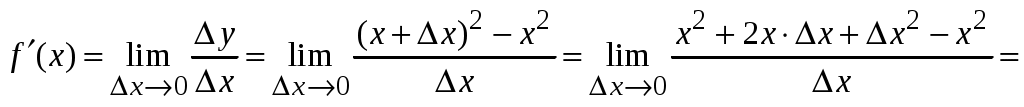 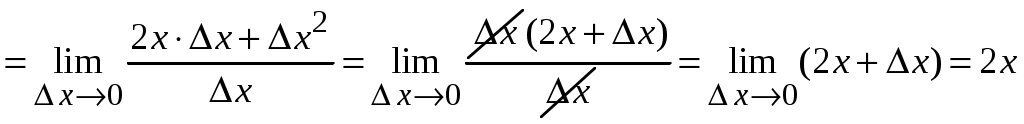 . .Ответ: |
