Дифференциальное исчисление функций одной действительной перемен. Методические указания к решению задач СанктПетербург Издательство спбгэту лэти 2009 удк 517. 22 (077)

• Название: Методические указания к решению задач СанктПетербург Издательство спбгэту лэти 2009 удк 517. 22 (077)
• Дата: 29.11.2020
• Размер: 1.04 Mb.
• Имя файла: Дифференциальное исчисление функций одной действительной перемен.doc
• Тип: Методические указания; #154951
• страница: 5 из 7

1.9.Производные высших порядков.

Производной второго порядка, или второй производной, функции называется производная от ее производной (которую называют первой производной).

Обозначения второй производной: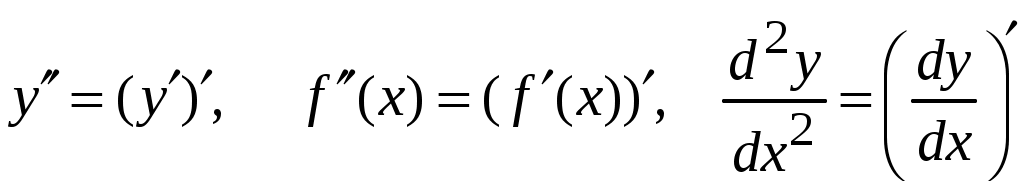

.

Механический смысл второй производной.

Если – закон прямолинейного движения точки, то – ускорение этого движения в момент времени x.

Аналогично определяются производные третьего, четвертого и более высоких порядков:

.

Производная n –ого порядка обозначается и так: .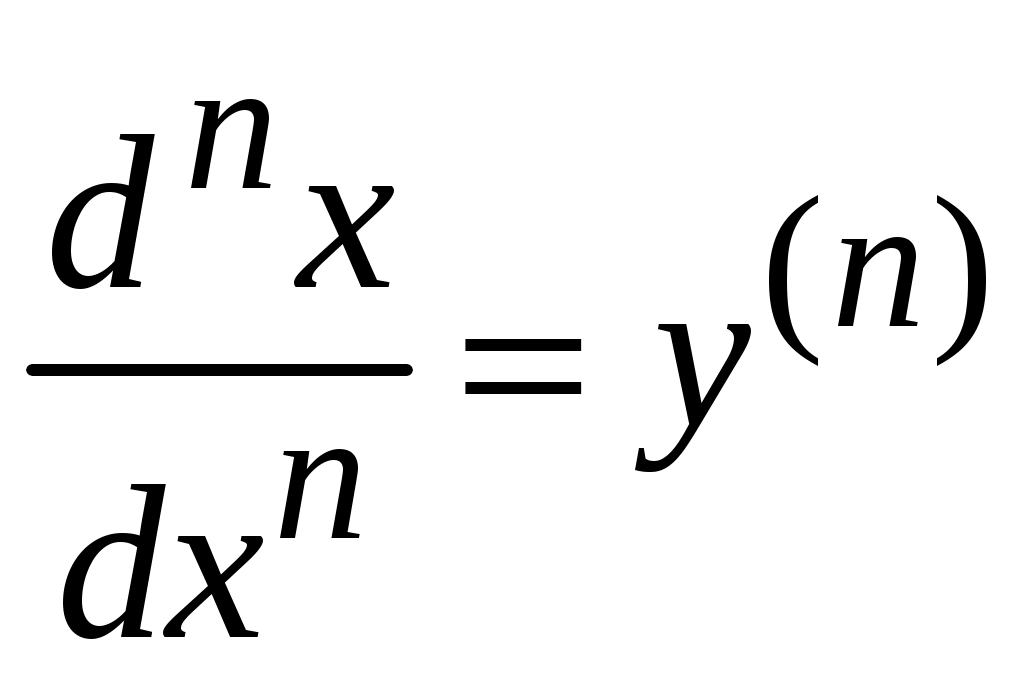

Если функция задана параметрически: 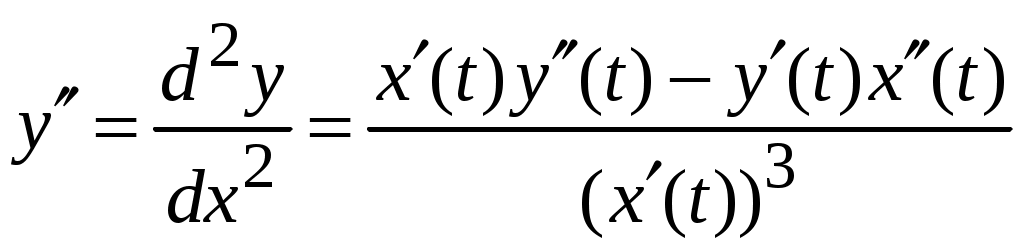, то ее вторая производная определяется формулой:

.

Пример ПРОИЗВОДНАЯ ФУНКЦИИ.15. Найти для функции .

Решение. Для того, чтобы вычислить значение третьей производной функции в точке , необходимо найти первую и вторую производные этой функции.

.

.

. [Подставляем в найденное выражение третьей производной значение ]

.

Ответ: {-6}.

Пример ПРОИЗВОДНАЯ ФУНКЦИИ.16. Найти вторую производную функции, заданной параметрически: .

Решение. Найдем первую и вторую производные для функций .

.

.

Воспользуемся формулой, приведенной выше: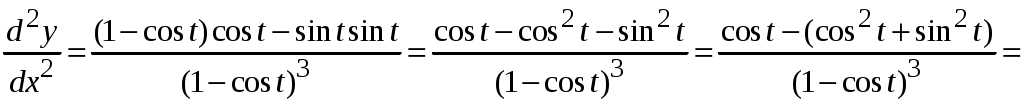



[воспользуемся тождеством, ] .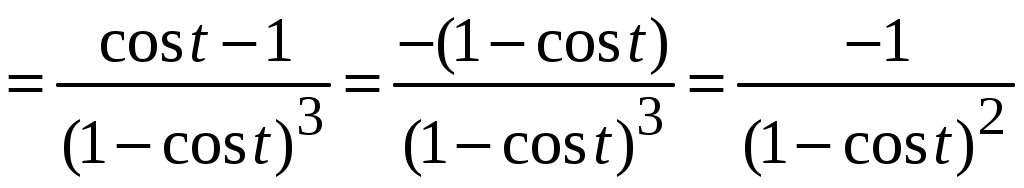

Ответ: .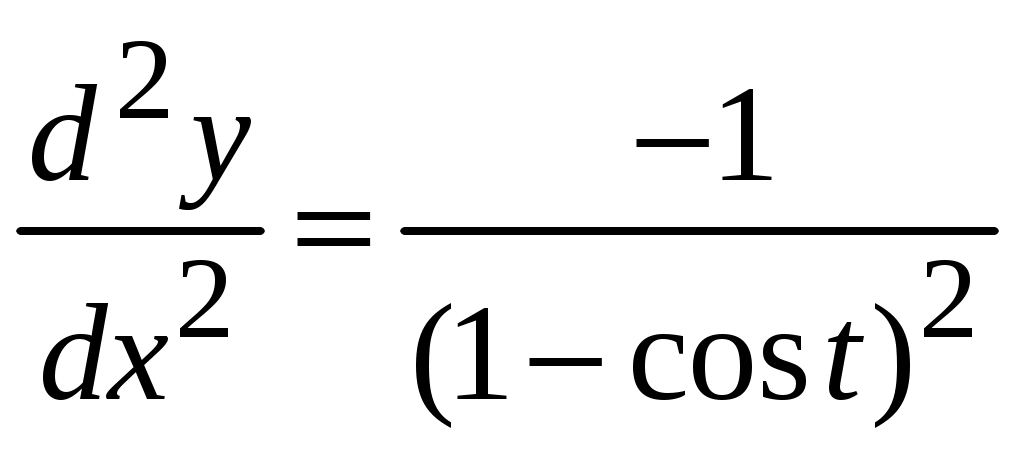

2.ПРИЛОЖЕНИЯ ПРОИЗВОДНЫХ

2.4.Дифференциал функции.

Пусть функция 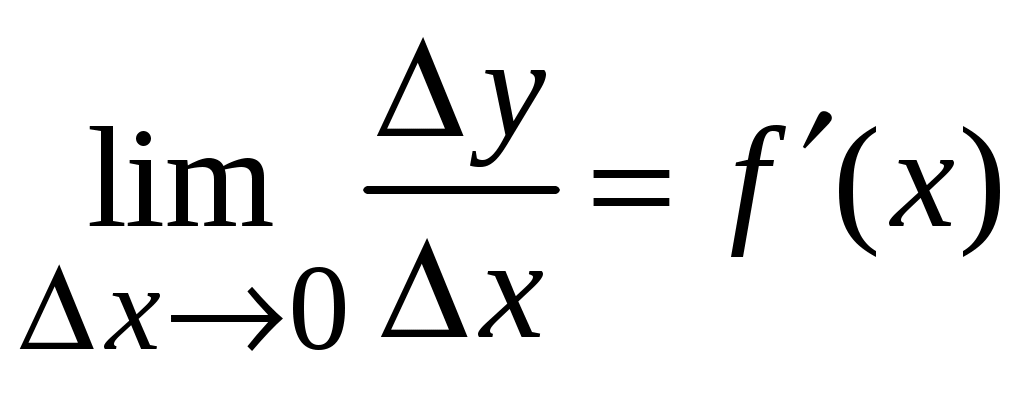, определенная в некотором промежутке имеет производную в точке x.

.

Тогда можно записать 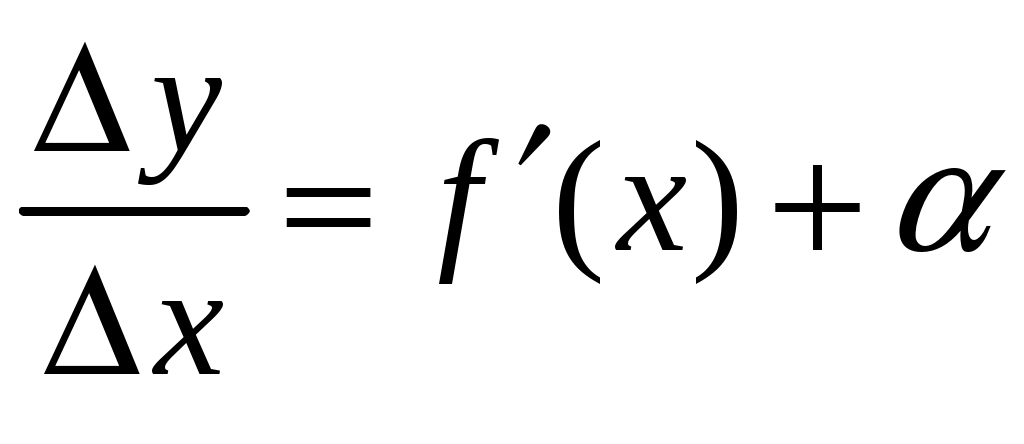, где при

Следовательно:

, где – бесконечно малая высшего порядка по сравнению с .

Определение: Дифференциалом функции в точке называется главная часть ее приращения, линейная относительно приращения аргумента. или .

Вычислим: . Следовательно

(2.1)

Пример ПРИЛОЖЕНИЯ ПРОИЗВОДНЫХ.17. Найти дифференциал данной функции:

a) ,

b)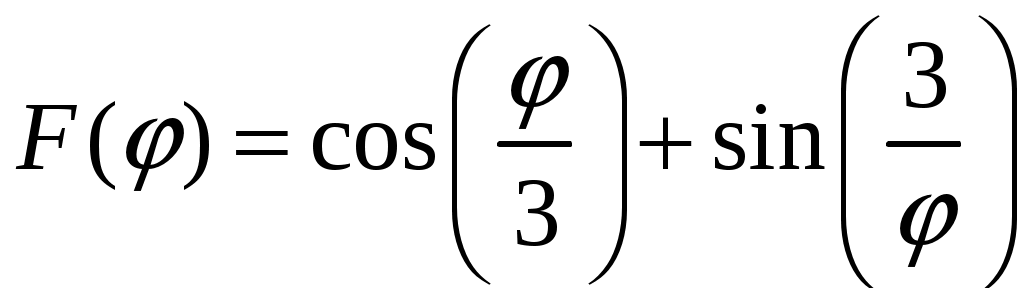

Решение: Находим производную данной функции и, умножив ее на дифференциал независимой переменной, получим искомый дифференциал данной функции:

a) ;

b)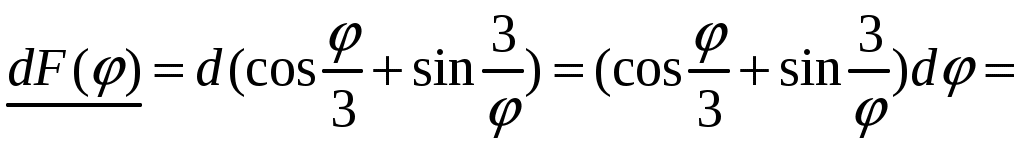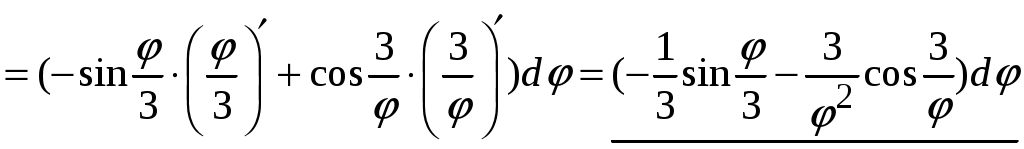

.

Геометрический смысл дифференциала.

Д 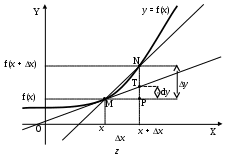ифференциал функции равен приращению ординаты касательной к графику функции в соответствующей точке, когда аргумент получает приращение .

Действительно на рисунке PN это приращение функции, а PT это приращение по касательной, или дифференциал.

Отметим, что может быть ,или – это зависит от направления выпуклости функции. тогда когда , т.е функция равна постоянной.

Дифференциал обладает свойствами, аналогичными свойствам производной.