Дифференциальное исчисление функций одной действительной перемен. Методические указания к решению задач СанктПетербург Издательство спбгэту лэти 2009 удк 517. 22 (077)

• Название: Методические указания к решению задач СанктПетербург Издательство спбгэту лэти 2009 удк 517. 22 (077)
• Дата: 29.11.2020
• Размер: 1.04 Mb.
• Имя файла: Дифференциальное исчисление функций одной действительной перемен.doc
• Тип: Методические указания; #154951
• страница: 6 из 7

2.5.Применение дифференциала в приближенных вычислениях.

Формулу можно записать так: и при достаточно малых значениях приращение функции может быть заменено ее дифференциалом с как угодно малой относительной ошибкой:

или , откуда

(2.2)

Это приближенное равенство применяется для приближенных вычислений , так как вычисление дифференциала функции значительно проще, чем вычисление ее приращения.

Пример ПРИЛОЖЕНИЯ ПРОИЗВОДНЫХ.18. Вычислить приближенное значение .

Решение: Пусть 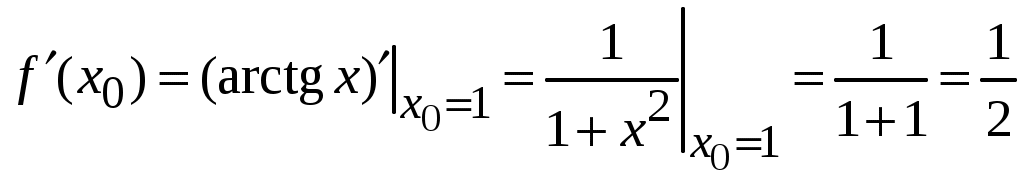есть частное значение функции при . Пусть , тогда

,

,

.

Подставляя найденные значения в формулу (2.2) получаем:

.

Ответ: 0,77.

2.6.Уравнения касательной и нормали к графику функции.

Уравнение касательной к линии в точке имеет вид . (2.3)

Нормалью к кривой в некоторой ее точке называется перпендикуляр к касательной в той же точке. Если 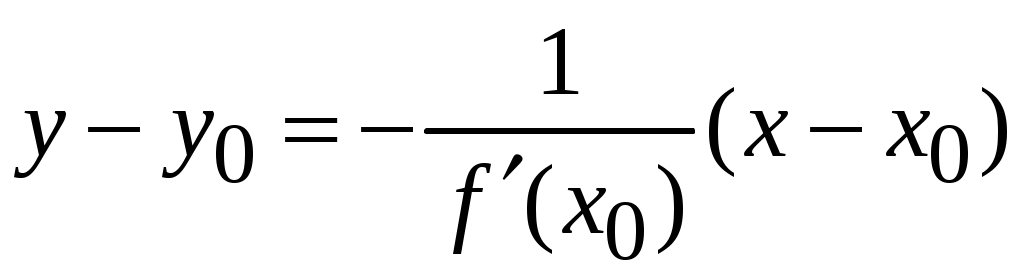, то уравнение нормали к линии в точке запишется так:

. (2.4)

Если в точке производная функции бесконечна, то есть , или не существует, то касательная в таком случае параллельна оси OY.



Угол между двумя пересекающимися кривыми 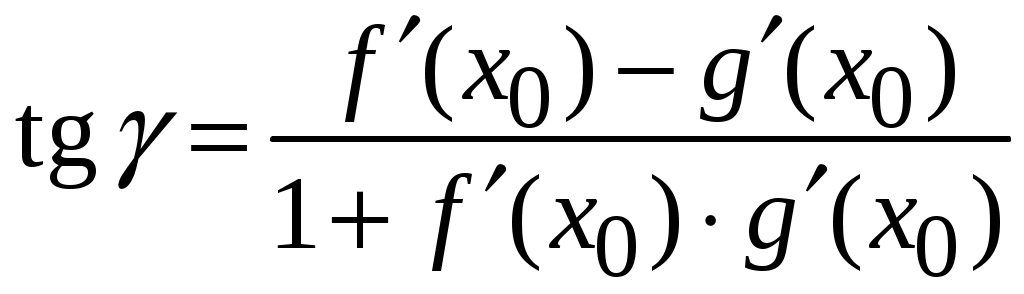и определяется как угол между двумя прямыми, касательными к кривым в точке их пересечения по формуле:

. (2.5)

Пример ПРИЛОЖЕНИЯ ПРОИЗВОДНЫХ.19. Найти угловой коэффициент касательной к графику функции в точке с абсциссой .

Решение. Угловой коэффициент касательной к графику функции в точке равен значению производной функции в этой точке. Найдем производную данной функции: .

Найдем значение производной в точке :

.

Ответ: 2.

Пример ПРИЛОЖЕНИЯ ПРОИЗВОДНЫХ.20. Найти угол между касательной к графику функции в точке с абсциссой и осью OX.

Решение. Тангенс угла между касательной к графику функции 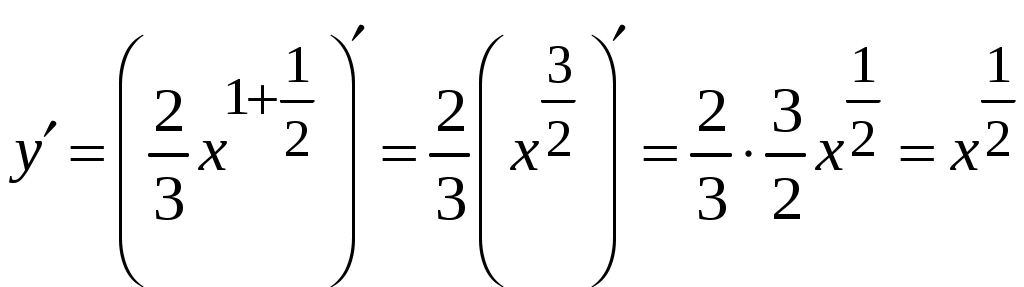в точке с абсциссой и осью OX это значение производной этой функции в данной точке. Найдем производную функции .

.

. Значит . Следовательно угол между касательной к графику функции и осью OX равен или .

Ответ: .

Пример ПРИЛОЖЕНИЯ ПРОИЗВОДНЫХ.21. Записать уравнение касательной к графику функции в точке с абсциссой .

Решение. Найдем производную заданной функции и ее значение в данной точке:

.

.

Найдем значение заданной функции в точке :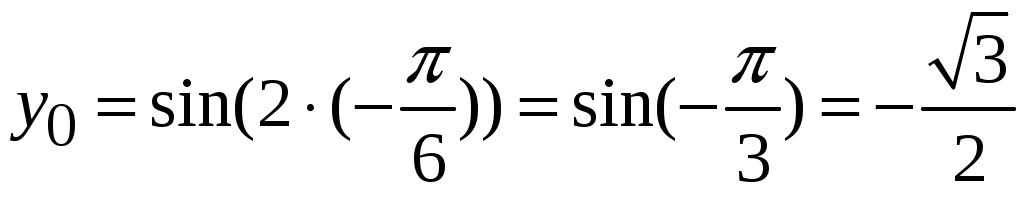

.

По формуле (2.3) запишем уравнение касательной: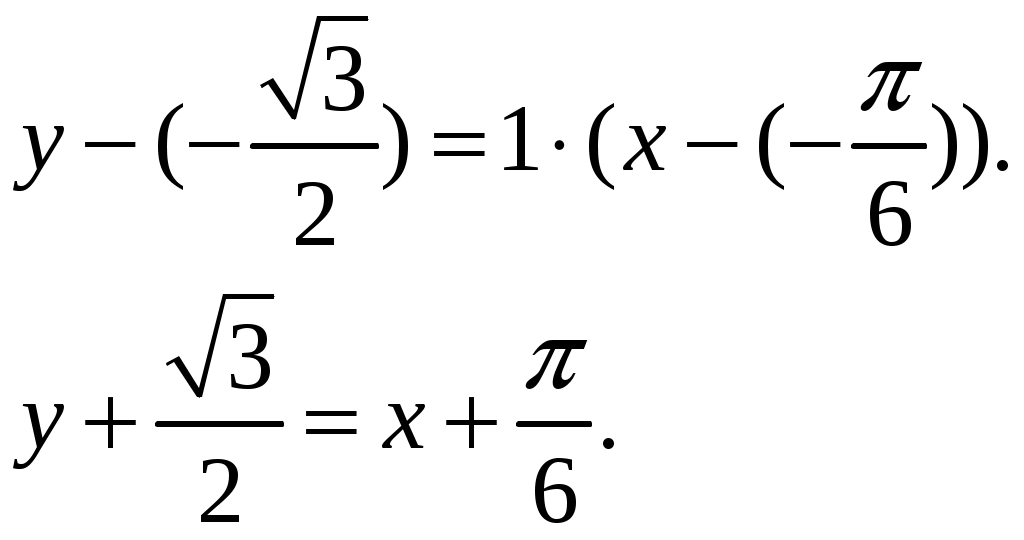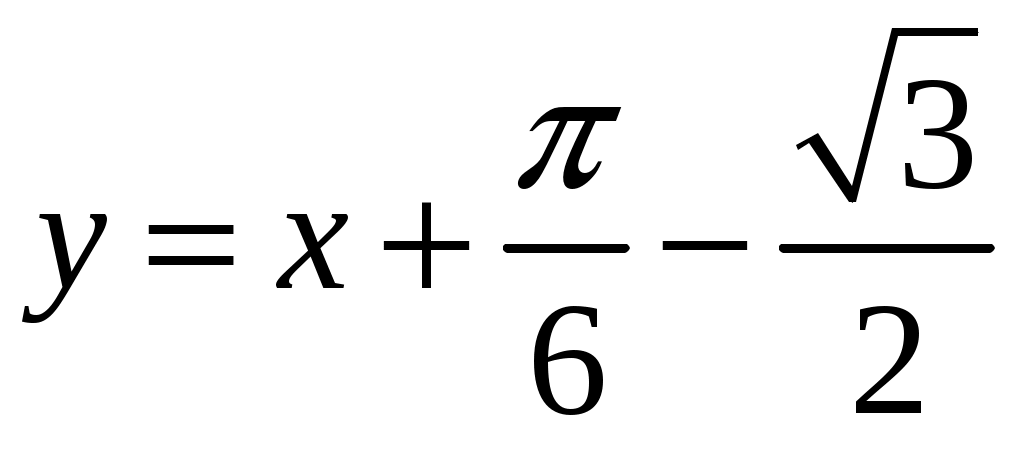



.

Пример ПРИЛОЖЕНИЯ ПРОИЗВОДНЫХ.22. Составить уравнение касательной и нормали к параболе в точке, где .

Решение: Подставляя в уравнение параболы заданную абсциссу касания , найдем ее ординату: .

Для определения углового коэффициента касательной найдем производную данной функции и ее значение при .

.Подставляя найденные значения в уравнения (2.3) и (2.4) запишем уравнения касательной и нормали:

– уравнение касательной;

– уравнение нормали.

Пример ПРИЛОЖЕНИЯ ПРОИЗВОДНЫХ.23. Найти угол, под которым пересекаются прямая и парабола .

Решение: Для того, что бы найти точку в которой пересекаются кривые надо совместно решить уравнения параболы и прямой: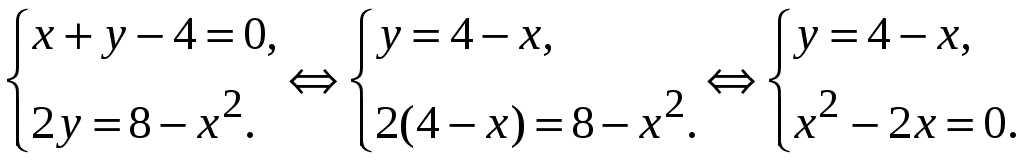



. Подставляем найденные значения в систему: . Следовательно, прямая и парабола пересекаются в двух точках: .

Далее находим угловые коэффициенты касательных к прямой и параболе:

;

.

Подставляя в найденные производные координаты точек пересечения, получаем угловые коэффициенты касательных:

.

.

Согласно формуле (2.5) получим: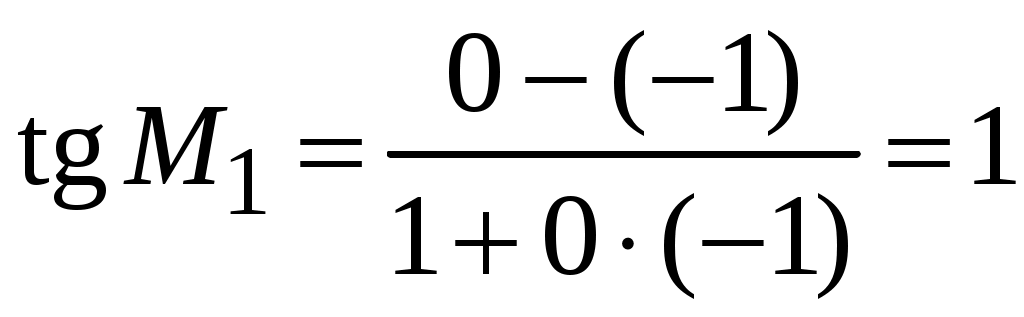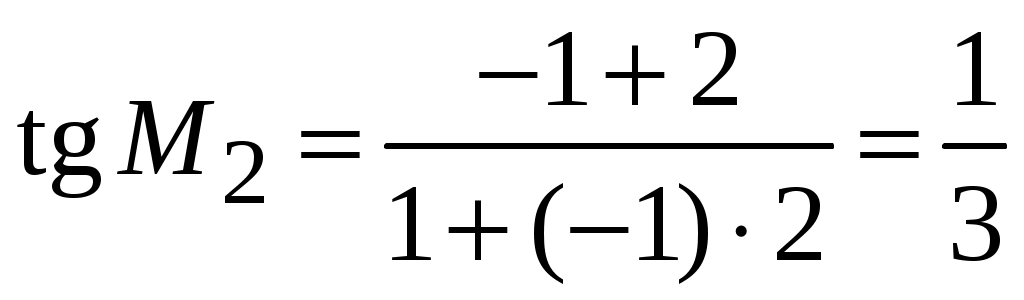

. .

. .

Ответ: , .