Дифференциальное исчисление функций одной действительной перемен. Методические указания к решению задач СанктПетербург Издательство спбгэту лэти 2009 удк 517. 22 (077)

• Название: Методические указания к решению задач СанктПетербург Издательство спбгэту лэти 2009 удк 517. 22 (077)
• Дата: 29.11.2020
• Размер: 1.04 Mb.
• Имя файла: Дифференциальное исчисление функций одной действительной перемен.doc
• Тип: Методические указания; #154951
• страница: 3 из 7

1.6.Основные правила дифференцирования.

Для того чтобы дифференцировать функции, обычно встречающиеся на практике, пользуются рядом простых и важных формул, которые обязательно знать наизусть.

Правила дифференцирования:

Пусть и – дифференцируемые функции. Тогда верны следующие формулы:

1. 
   , если c – постоянная величина (константа).
   
2. 
   (ПРОИЗВОДНАЯ ФУНКЦИИ.1)
   

Пример ПРОИЗВОДНАЯ ФУНКЦИИ.2. Найти производную .

Решение: Пользуясь таблицей производных и правилом (1.1) находим: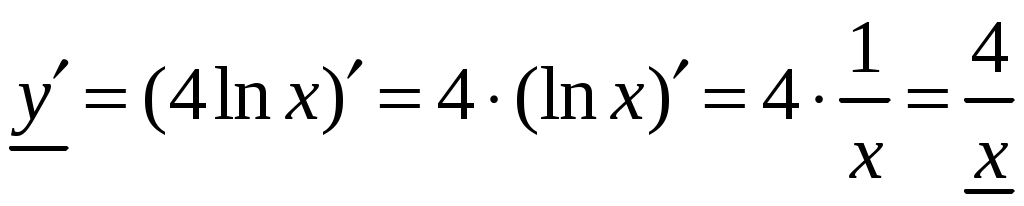

3. 
   (ПРОИЗВОДНАЯ ФУНКЦИИ.2)
   

Пример ПРОИЗВОДНАЯ ФУНКЦИИ.3. Найти производную функции .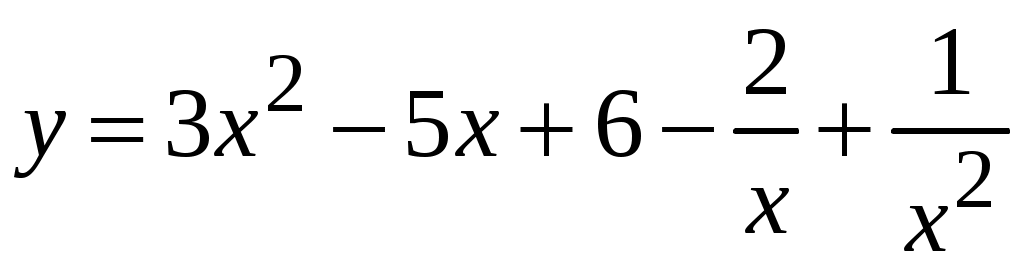

Решение. Так как по правилу (1.2) производная от суммы функций равна сумме производных от каждой функции, то можем записать: .

Продифференцируем выражения, стоящие в скобках, пользуясь таблицей производных.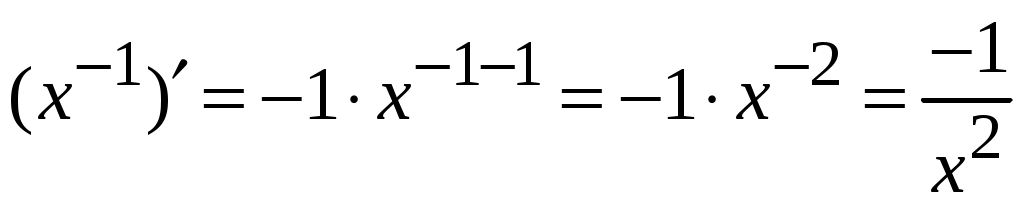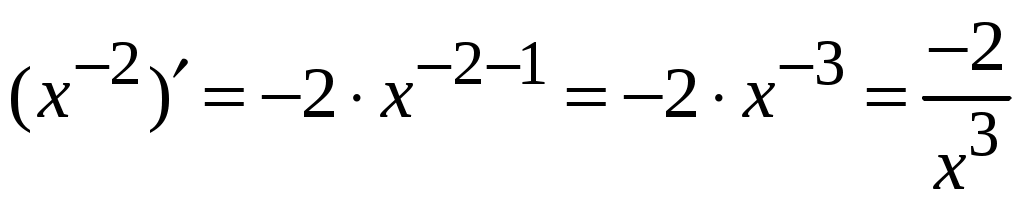

,

,

, так как 6 – константа ,

,

.

В итоге получим: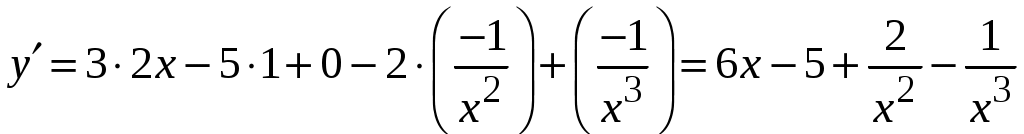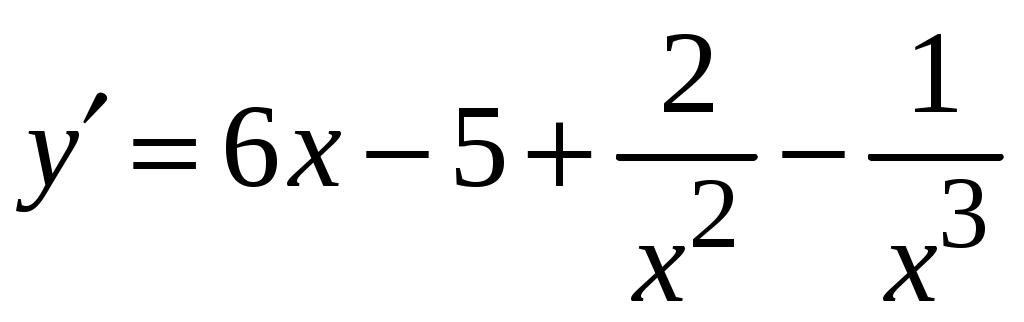

.
.

Пример ПРОИЗВОДНАЯ ФУНКЦИИ.4. Найти производную функции .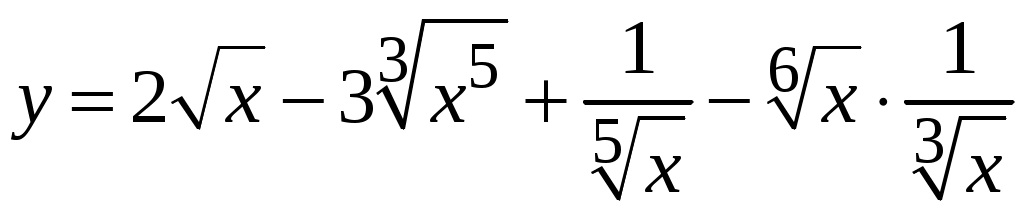

Решение. Так как по правилу (1.2) производная от суммы функций равна сумме производных от каждой функции, то можем записать: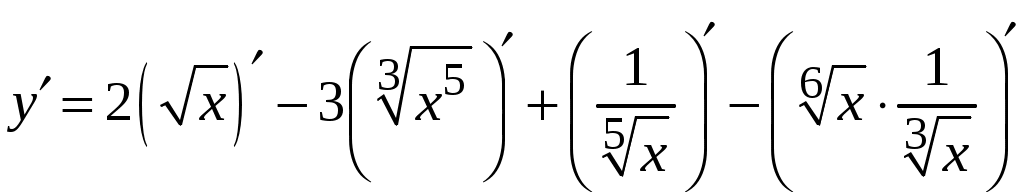

.

Продифференцируем каждое слагаемое по отдельности, для удобства записав функции в виде степени с дробным показателем.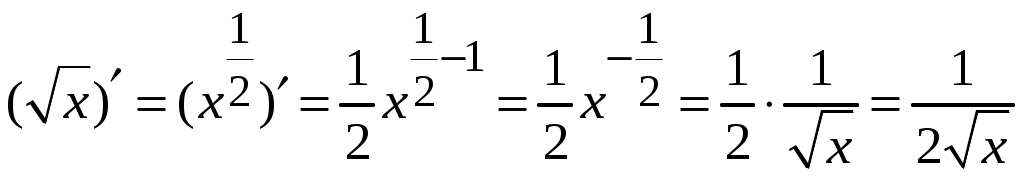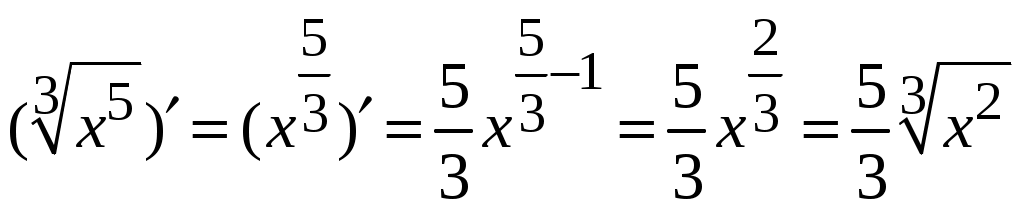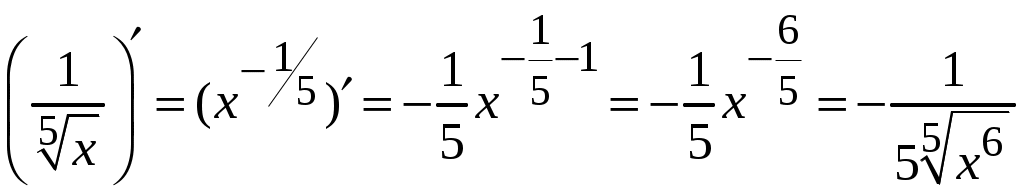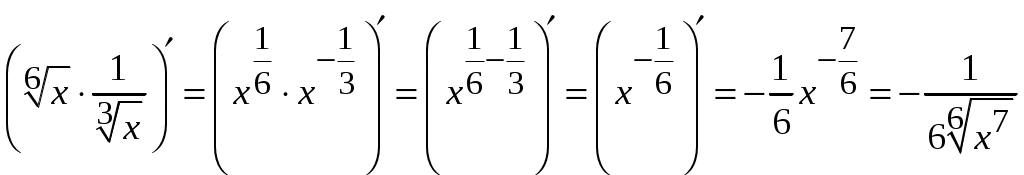

.

.

.

.

В итоге получим: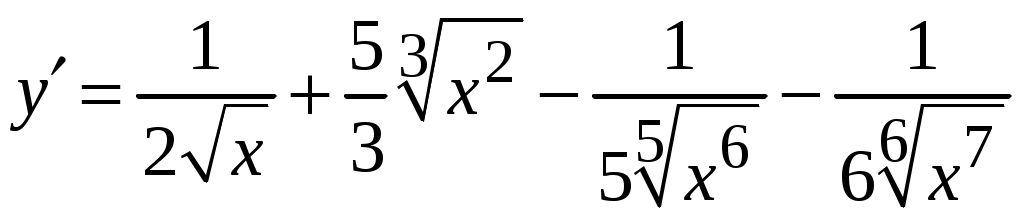

.

4. 
   (ПРОИЗВОДНАЯ ФУНКЦИИ.3)
   

Пример ПРОИЗВОДНАЯ ФУНКЦИИ.5. Найти производную функции .

Решение. Воспользуемся правилом (1.3) для дифференцирования произведения двух функций.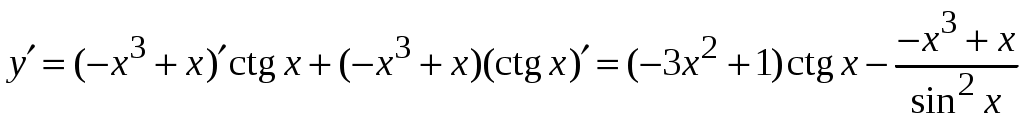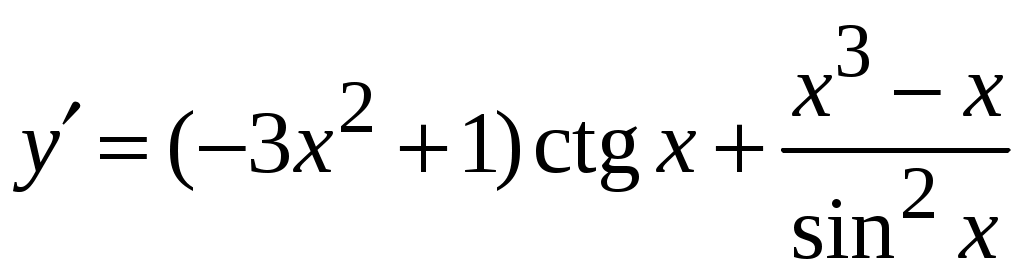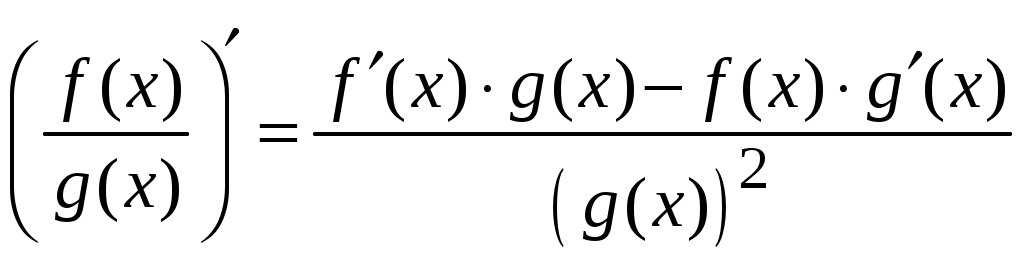

.

.

5. 
   (ПРОИЗВОДНАЯ ФУНКЦИИ.4)
   

Пример ПРОИЗВОДНАЯ ФУНКЦИИ.6. Найти производную функции .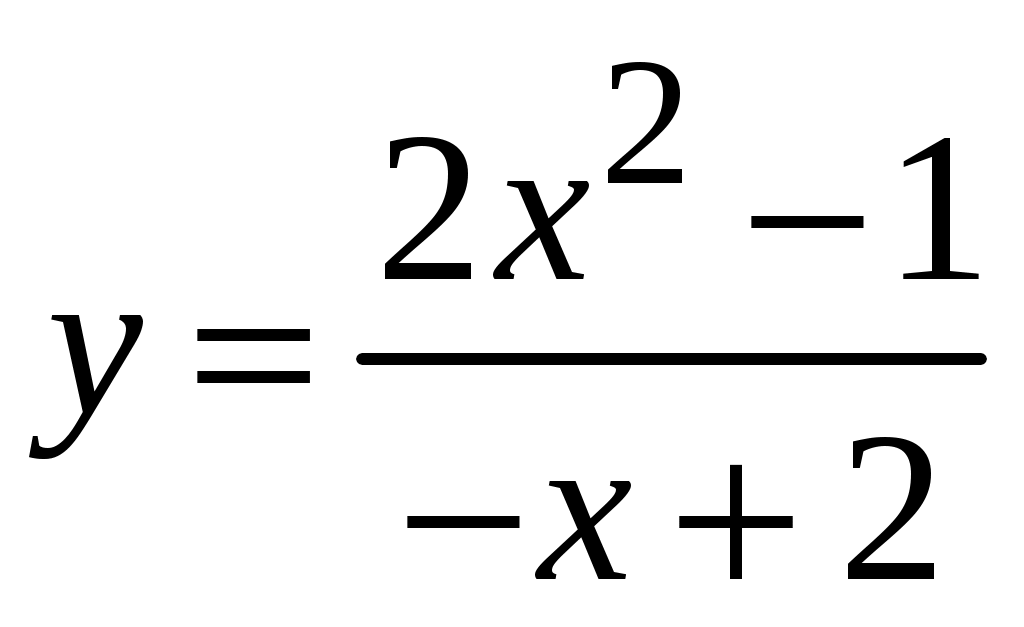

Решение. Воспользуемся правилом (1.4) для дифференцирования частного двух функций.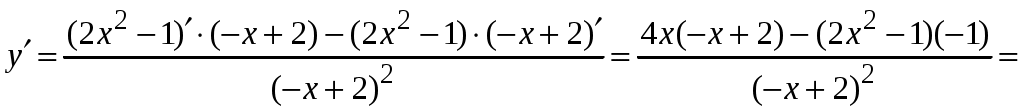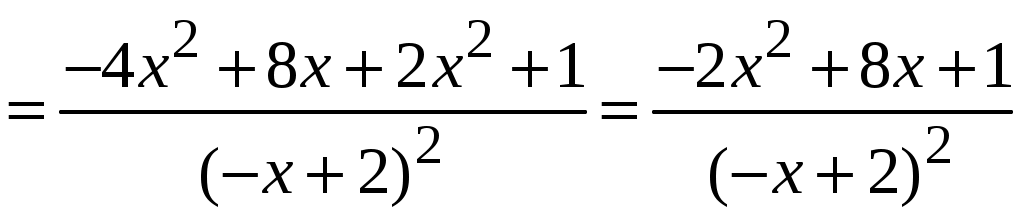





.

В итоге: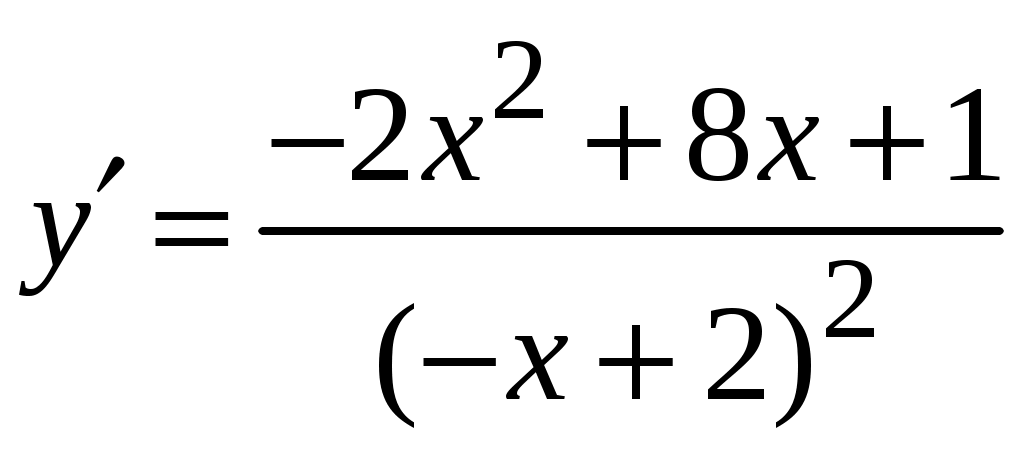

.

6. 
   Если , а то функция называется сложной функцией и, если обе функции дифференцируемы, то дифференцируема и сложная функция, а ее производную можно найти по формуле:
   (ПРОИЗВОДНАЯ ФУНКЦИИ.5)
   

Таким образом, производная сложной функции равна производной по промежуточному аргументу, умноженной на производную этого аргумента по независимой переменной. Коротко можно сказать так: производная сложной функции равна произведению производных всех ее составляющих.

Пример ПРОИЗВОДНАЯ ФУНКЦИИ.7. Найти производную функции .

Эту функцию можно рассматривать как сложную функцию, составленную из кубической функции и квадратичной . Тогда по правилу (1.5) производная сложной функции находится следующим образом:

.

Вспомним, что функция – промежуточная и введена нами для удобства нахождения производной от сложной функции, теперь нам надо вернуться обратно, подставив вместо этой промежуточной функции ее выражение: .

.

В дальнейшем промежуточная функция явно вводиться в решение не будет, но надо иметь в виду, что мысленно мы ее обязательно обозначаем.

Пример ПРОИЗВОДНАЯ ФУНКЦИИ.8. Найти производную функции .

Решение: Для того, чтобы найти производную данной функции надо воспользоваться правилом (1.5), так как эта функция является сложной.

Промежуточной функцией в данном примере будет функция

.

.

Пример ПРОИЗВОДНАЯ ФУНКЦИИ.9. Найти производную функции .

Решение: В данном случае промежуточная функция – степенная, применяя таблицу производных, получаем:

.

.

Пример ПРОИЗВОДНАЯ ФУНКЦИИ.10. Найти производную функции .

Решение: И в данной сложной функции промежуточная функция тоже степенная:

.

.

Пример ПРОИЗВОДНАЯ ФУНКЦИИ.11. Найти производную функции .

Решение: Данная сложная функция состоит из двух промежуточных функций. Дифференцируем, применяя правило (1.5).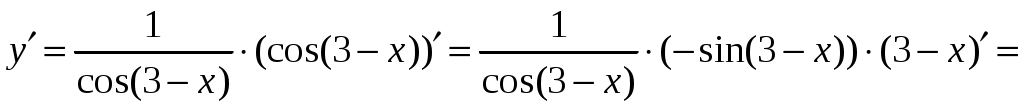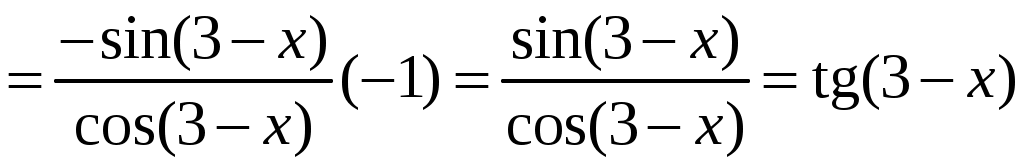



.

.