реферат. Методические указания Абакан 2011
 Скачать 0.86 Mb.
|
|
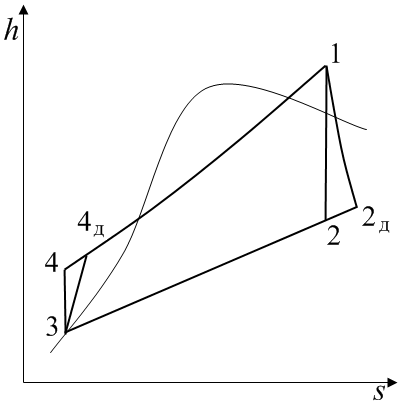
Задача 8 По заданным параметрам свежего пара p1, t1 и давлению в конденсаторе p2 на h,s – диаграмме строят график процесса расширения пара в турбине – линии 1-2 и 1-2д (рис.6). Изоэнтропный (теоретический) процесс изображается вертикальной прямой 1-2, точка 2 лежит на заданной изобаре p2. Располагаемый теплоперепад турбины Ho, кДж/кг, равен разности энтальпий пара в точках 1 и 2 цикла:  .Удельная работа турбины lT, кДж/кг:  ,где  – внутреннего относительного КПД турбины.Энтальпия пара на выходе из турбины, кДж/кг:  .Точка 2д, соответствующая состоянию пара на выходе из турбины в действительном процессе, строится по двум параметрам p2 и h2д. Определяют недостающие параметры пара в точке 2д: температуру t2д, степень сухости x2д, удельный объем v2д удельную энтропию s2д. Энтальпия конденсата в точке 3 цикла может быть найдена по справочнику [1] по известному давлению в конденсаторе p2 или приближенно рассчитана по формуле:  ,где  – удельная теплоемкость конденсата, можно принять ск=4,19 кДж/(кг·К);  – температура конденсата, оС (t3=t2д). Энтальпия питательной воды h4 в теоретическом цикле превышает энтальпию конденсата на величину удельной работы насоса при изоэнтропном повышении давления.  , где vв – удельный объем воды, можно принять vв=0,001м3/кг; p4, p3 – давления воды в точках 4 и 3 цикла, кПа.
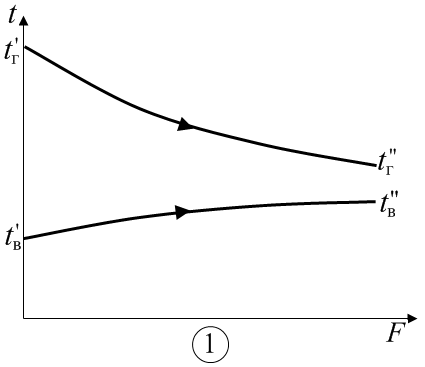
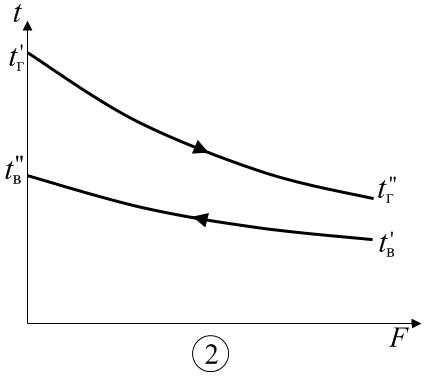
где Т1 и Т2 – максимальная и минимальная абсолютные температуры рассматриваемого цикла, К. Внутренний относительный КПД комплекса турбина–насос:  Внутренний абсолютный КПД паротурбинной установки:  .Необходимый расход пара в турбину, кг/с:  .Задача 9 Плотность теплового потока через многослойную плоскую стенку, каковой можно считать рассматриваемую стену помещения, определяют по формуле, Вт/м2: 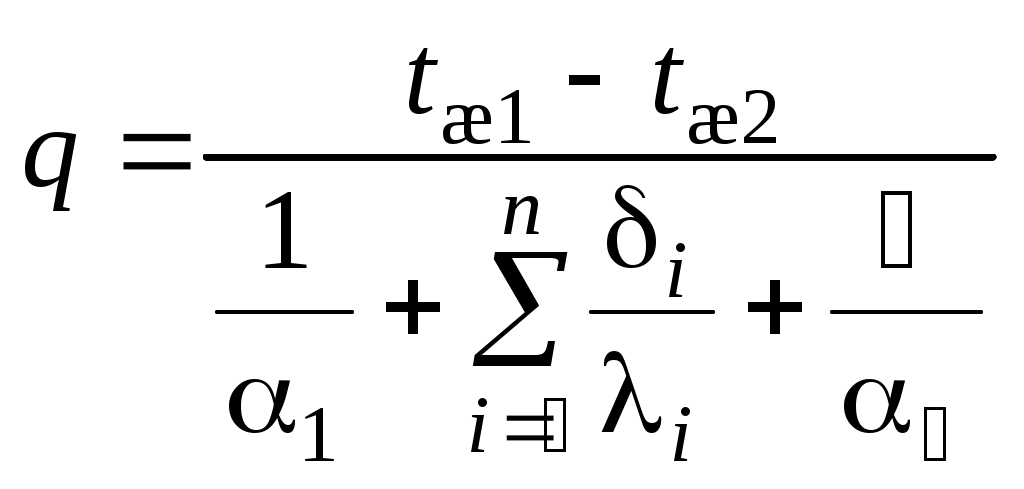 ,где i– номер слоя; n – число слоев стенки. При стационарном режиме теплопередачи температуры на внешних поверхностях стены и на границах между ее слоями могут быть последовательно найдены из выражений плотности теплового потока. Плотность теплового потока на поверхности стены, Вт/м2:  .Плотность теплового потока в твердом слое, Вт/м2:  .Общее количество теплоты, переданной через стену, Дж:  ,где F – площадь стены, м2; τ – продолжительность теплообмена, с. Задача 10 Нихромовый электрический нагреватель можно рассматривать как неограниченный по длине однородный цилиндрический стержень с внутренними источниками теплоты. Расчёты удобно проводить для участка стержня длиной 1м. Электрическое сопротивление такого участка R, Ом/м, выражается через удельное сопротивление нихрома ρ, Ом·мм2/м, и площадь поперечного сечения нагревателя  , мм2, то есть: ,где rо – радиус нагревателя, мм. Количество теплоты, отдаваемой окружающей жидкости через поверхность стержня длинной 1м, при стационарном режиме равно джоулевой теплоте, выделяемой внутри участка нагревателя, Вт/м:  ,Мощность внутренних источников теплоты в цилиндрическом стержне, Вт/м3:  ,где r – радиус нагревателя, м. Температуру в любой точке бесконечно длинного цилиндра с внутренними источниками теплоты находят по известной формуле, оС:  ,где r – расстояние от оси цилиндра до рассматриваемой точки, м. Задача 11 Цилиндр конечных размеров можно представить как тело, образованное пересечением неограниченной пластины толщиной 2δ и бесконечно длинного цилиндра диаметром d. В таком случае безразмерная температура в любой точке цилиндра конечных размеров равна произведению соответствующих безразмерных температур неограниченной пластины и бесконечного цилиндра. Критерии Био и Фурье для неограниченной пластины:  ,  ,где a – коэффициент температуропроводности материала цилиндра, м2/с. (  ).По номограммам [6,9] в зависимости от Bi и Fo определяют безразмерные температуры в центре неограниченной пластины θo и на ее поверхности θδ. Критерии Био и Фурье для цилиндра бесконечной длины:  ,  .По номограммам находят безразмерные температуры на оси θz и на поверхности θr бесконечного цилиндра. Вычисляют безразмерные температуры в заданных точках 1 – 4 цилиндра конечных размеров.  ,  ,  ,  .От безразмерных нетрудно перейти к размерным температурам t, oC, исходя из соотношения  .Задача 12 Тепловой поток, приходящийся на 1м длинны однослойной цилиндрической стенки ql, Вт/м, вычисляют по известной формуле: 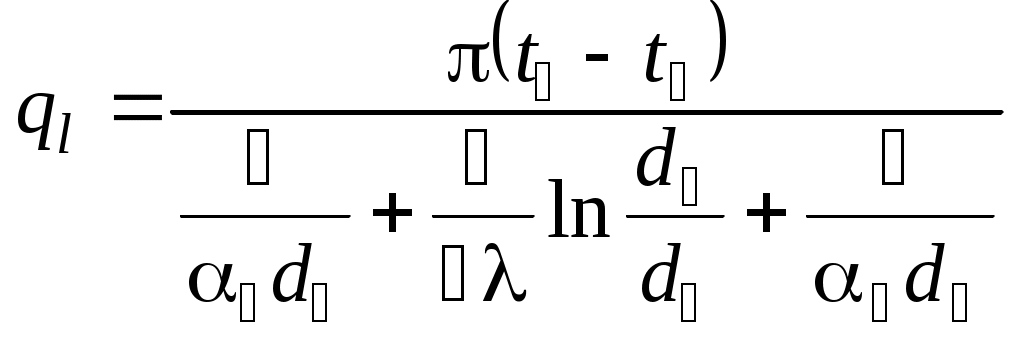 ,где t1 и t2 – температура горячей и холодной подвижных сред (воды и воздуха), °С; d1 и d2 – внутренний и внешний диаметры цилиндрической стенки, м; α1 и α2 – коэффициенты теплоотдачи на внутренней и внешней поверхностях, Вт/(м2·°С); λ – коэффициент теплопроводности материала стенки, Вт/(м·°С). Некоторые величины, входящие в формулу (t1, t2, d1, λ), даны в условии задачи. Внешний диаметр трубы d2 нетрудно определить, зная внутренний диаметр и толщину стенки. Коэффициенты теплоотдачи α1 и α2 находят из соответствующих критериальных уравнений. Для подбора подходящего критериального уравнения и вычисления коэффициента теплоотдачи на внутренней поверхности трубы необходимо выяснить режим течения воды. С этой целью находят число Рейнольдса:  ,где νж – кинематический коэффициент вязкости воды, м/с2. Если Reж > 10000, то режим турбулентный. В таком случае рекомендуется следующее критериальное уравнение:  Коэффициент теплоотдачи на внутренний поверхности трубы рассчитывают исходя из найденного числа Нуссельта:  где λж – коэффициент теплопроводности воды при заданной температуре t1, Вт/(м·°С). Критериальное уравнение для вычисления коэффициента теплоотдачи на внешней поверхности трубы подбирают в зависимости от величины комплекса (Gr ∙Pr)в. 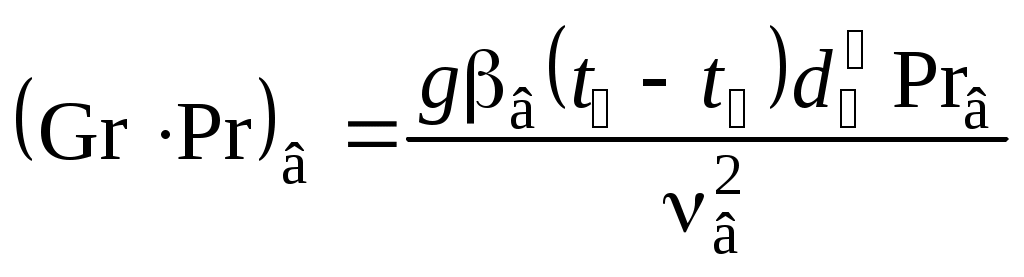 ,где g = 9,81м/c2 – ускорение свободного падения; νв – кинематический коэффициент вязкости воздуха, м2/с; β = 1/(t2 + 273) – коэффициент теплового расширения, К-1; Prв – число Прандтля воздуха. Если численное значение комплекса (Gr ·Pr)в находится в пределах 103 – 109, то расчёт коэффициента теплоотдачи от внешней поверхности горизонтальной трубы воздуху производят по критериальному уравнению  Тогда   где λв – коэффициент теплопроводности воздуха, Вт/(м ·°С). Задача 13 Паропровод, уложенный в закрытом канале, можно рассматривать как систему двух тел, одно из которых находится внутри другого. Лучистый тепловой поток Q1-3, Вт/м, с поверхности участка неизолированной трубы длинной 1 м на стенки канала выражается формулой 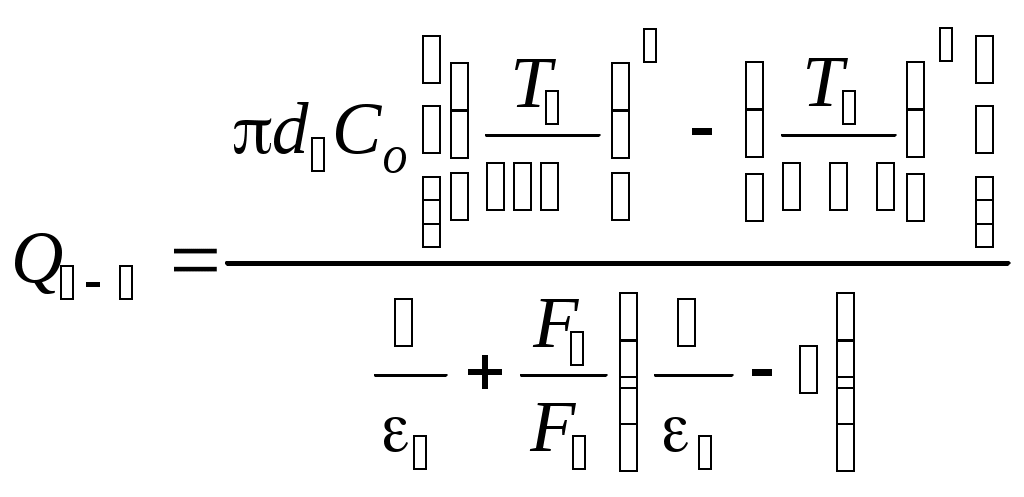 ,где С0 = 5,67 Вт/(м2·К4) – коэффициент излучения абсолютно черного тела; T1 и T3 – абсолютные температуры поверхностей паропровода и канала, К; F1/F3 – отношение площадей поверхностей паропровода и канала. В рассматриваемом случае F1/F3 = πd1/4δ. Если паропровод окружен защитным экраном, то при стационарном режиме количество теплоты, передаваемой с поверхности паропровода экрану, будет равно теплоте, отводимой от экрана на стенки канала, то есть Q1-2 = Q2-3. Необходимо написать уравнение теплового баланса для экрана при условии, что конвекция воздуха в канале пренебрежимо мала, и основным видом теплопереноса является излучение. Определить из уравнения абсолютную температуру экрана. После чего нетрудно будет вычислить тепловые потери экранированного паропровода. Задача 14 Количество трубок в пучке теплообменного аппарата n может быть выражено и вычислено из уравнения теплопередачи:  ,где Qв – теплота, воспринимаемая водой, Вт; l – длина трубки, м; Δt – средняя разность температур теплоносителей, °С; kl – линейный коэффициент теплопередачи трубки, Вт/(м·°С). Теплота, воспринимаемая водой, находится по формуле: 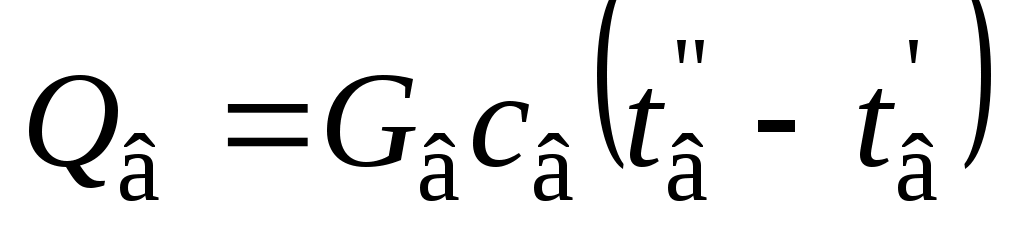 .Теплота, отдаваемая газом Qг, превышает Qв вследствие тепловых потерь теплообменника, которые, согласно условию задачи, равны 5%.  .Средняя разность температур теплоносителей в общем случае: 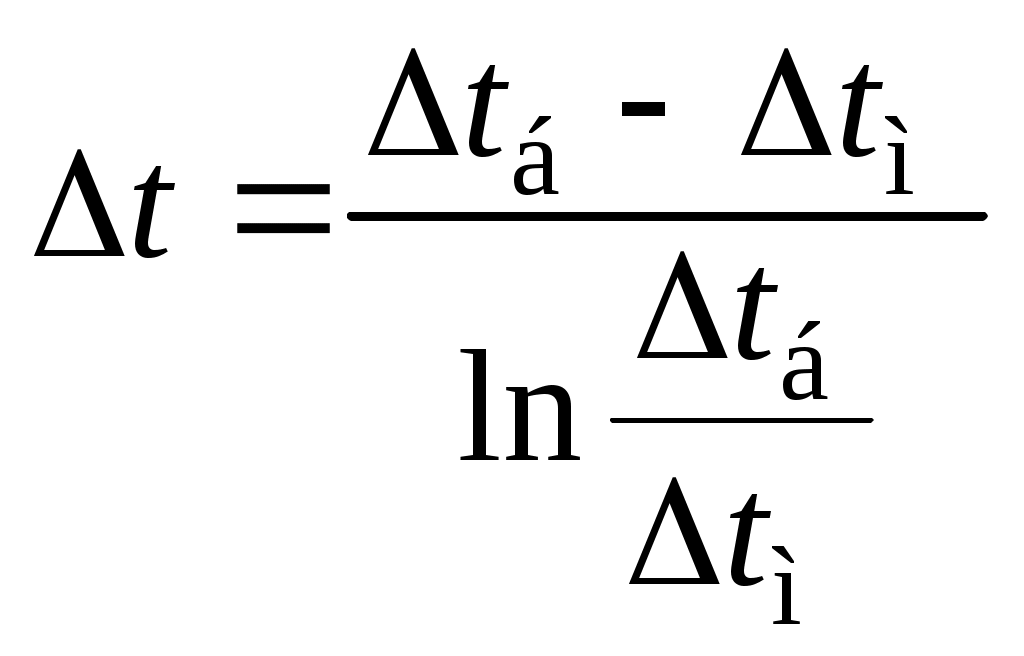 , где Δtб и Δtм – большая и меньшая разности температур теплоносителей в теплообменном аппарате. Для вычисления Δtб и Δtм кроме известных по условию задачи температур tв’, tв”, tг’ необходима температура газа, покидающего аппарат tг”, которая находится из равенства: 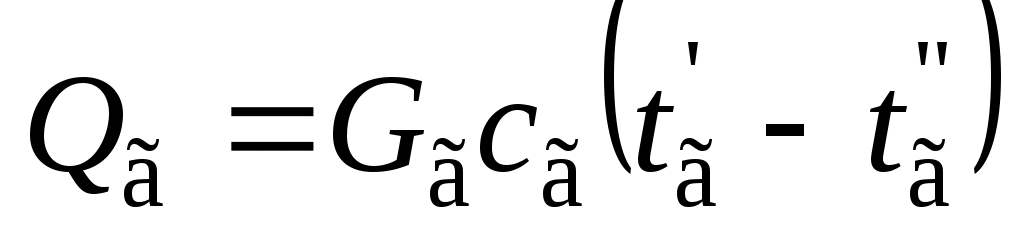 Разности температур Δtб, Δtм, Δt, а также количество трубок теплообменного аппарата n определяются дважды – для прямоточной и противоточной схем движения теплоносителя. На рис.7 показаны формы графиков изменения температуры теплоносителей в теплообменнике при их прямоточном и противоточном движении.
Линейный коэффициент теплопередачи трубки рассчитывается по известной формуле, Вт/(м·°С).: 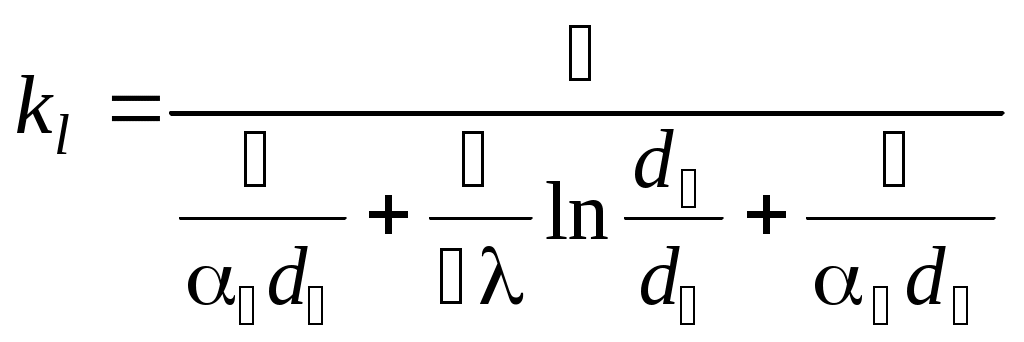 По результатам решения задачи следует сделать вывод, которая из двух схем движения теплоносителей, прямоточная или противоточная, эффективнее. ПРИЛОЖЕНИЕ Таблица 15. Средние молярные изобарные теплоемкости газов
Таблица 16. Физический свойства сухого воздуха при p=0,1 МПа
Таблица 17. Физические свойства воды на линии насыщения
Таблица 18 Энтальпия воды h’ и сухого пара h’’, кДж/кг, в состоянии насыщения
ЗАКЛЮЧЕНИЕ Знания по теоретическим основам теплотехники будут полезны студенту при изучении профильных дисциплин учебного курса, а также в его дальнейшей работе по выбранной специальности или направлению. Важной составной частью учебного процесса является самостоятельная работа при выполнении расчетных заданий. Результатом решения задач по технической термодинамике и теории теплообмена должно стать закрепление теоретического материала, а также приобретение практических навыков теплотехнических расчетов. Приведенные в методических указаниях рекомендации и необходимый справочный материал позволят студенту избежать перерасхода времени на выполнение контрольной работы. Предполагаемые затраты времени на работу из 4–5 задач составляют 8–10 часов. БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Александров, А. А. Таблицы теплофизических свойств воды и водяного пара: справочник / А. А. Александров, Б. А. Григорьев. – М.: Издательский дом МЭИ, 2006.– 168 с. 2. Андреев, И. И. Теоретические основы теплотехники. Введение в термодинамику: учеб. пособие / И. И. Андреев.– Красноярск: ИПЦ КГТУ, 2001. – 108 с. 3. Андрианова, Т.А. Сборник задач по технической термодинамике: учеб. пособие для вузов /Т.А. Андрианова, Б.В. Дзампов, В.Н. Зубарев, С.А. Ремизов.- М.: Энергоиздат, 1981.– 240 с. 4. Видин, Ю.В. Теплотехника : учеб. пособие / Ю.В. Видин. – Красноярск: ИПЦ КГТУ, 2004 (Красноярск). – 88 с. 5. Ерофеев, В. Л. Теплотехника: учебник для вузов / В. Л. Ерофеев, П. Д. Семенов, А. С. Пряхин. – М.: Академкнига, 2008. – 488 с. 6. Исаченко, В. П. Теплопередача: учебник для вузов / В. П. Исаченко, В. А. Осипова А.С. Сукомел. – М.: Энергоиздат, 1981.– 416 с. 7. Кириллин, В.А Техническая термодинамика: учебник для вузов / В. А. Кириллин, В.В. Сычев, А.Е. Шейндлин. – М.: Энергоатомиздат, 1983.– 416 с. 8. Кудинов, В.А. Техническая термодинамика: учеб. пособие для вузов / В.А. Кудинов, Э.М. Карташов. – М.: Высшая школа, 2001. – 261 с. 9. Нащокин, В.В. Техническая термодинамика и теплопередача: учеб. пособие для вузов. / В.В. Нащокин. – М.: Высш. школа, 1980. – 469 с. 10. Немченко, Н. И. Термодинамика: учеб. пособие / Н.И. Немченко; Сиб. федер. ун-т, ХТИ – филиал СФУ.– Абакан: РИО ХТИ – филиала СФУ, 2011.– 140 с. 11. Цветков Ф. Ф. Тепломассообмен: учеб. пособие для вузов / Ф. Ф. Цветков, Б. А. Григорьев. – М.: Издательство МЭИ, 2005.– 550 с. ОГЛАВЛЕНИЕ
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
, кДж/кг, определяют с учетом внутреннего относительного КПД насоса 
:
.
.
,
