лабораторные работы по физике 11 класс. Методические указания для подготовки к выполнению лабораторных работ по курсу физики для студентов
 Скачать 6.72 Mb. Скачать 6.72 Mb.
|
V. Лабораторная работа № 5ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА МЕТОДОМ МАГНЕТРОНА 1. Цель работы: определение удельного заряда электрона с помощью магнетрона. 2. Подготовка к работе: прочитать в учебниках параграфы [1] §§ 4.2, 21.2, 23.3; [2] §§ 18, 19, 114; [3] §§ 214, 218. Для выполнения работы студент должен знать: а) понятие об удельном заряде электрона; б) понятие силы Лоренца; в) момент силы относительно неподвижной точки и оси; г) момент импульса относительно неподвижной точки и оси; д) принцип действия приборов, используемых в данной лабораторной установке; е) устройство и принцип работы двухэлектродной электронной лампы (магнетрона); ж) методику определения удельного заряда электрона; з) экспериментальное определение критического значения тока в соленоиде; и) изучить принципиальную электрическую схему и блок-схему лабораторной установки. 3. Выполнение работы 3.1. Описание лабораторного стенда На рис. 5.1 приведена блок-схема лабораторной установки, состоящая из модуля ФПЭ-03, источника питания ИП и миллиамперметра РА. 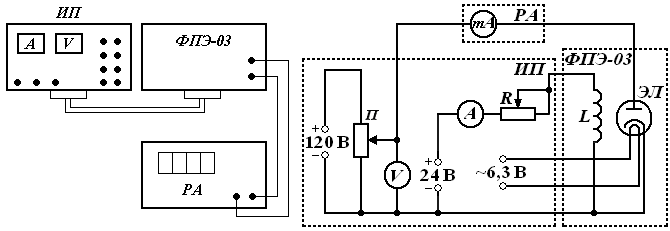 Рис. 5.1. Блок-схема установки Рис. 5.2. Принципиальная электрическая схема установки На рис. 5.2 приведена принципиальная электрическая схема лабораторной установки. Модуль ФПЭ-03 состоит из двухэлектродной электронной лампы ЭЛ и соленоида L. Источник питания ИП состоит из потенциометра П, переменного сопротивления R, амперметра А и вольтметра V. Напряжение на аноде электронной лампы ЭЛ регулируется с помощью потенциометра П. Анодный ток измеряется миллиамперметром mA. Переменное сопротивление R регулирует ток соленоида L, который измеряется амперметром А. На накал катода лампы ЭЛ подаётся напряжение 6,3 В. Вольтметр V показывает напряжение на аноде лампы ЭЛ. 3.2. Методика измерений и расчёта Для изучения движения электрона и измерения его удельного заряда используется специальная двухэлектродная электронная лампа (магнетрон), электроды которой представляют собой коаксиальные цилиндры. Данная лампа помещается внутри соленоида. При этом ось лампы совпадает с осью соленоида. Электроны, вылетающие из катода лампы, при отсутствии тока в соленоиде под действием анодного напряжения движутся радиально к аноду. При подключении источника тока к соленоиду в лампе создаётся магнитное поле, направленное вдоль оси соленоида и параллельное оси лампы. На электроны, вылетающие из катода, действует сила Лоренца (рис. 5.3) где 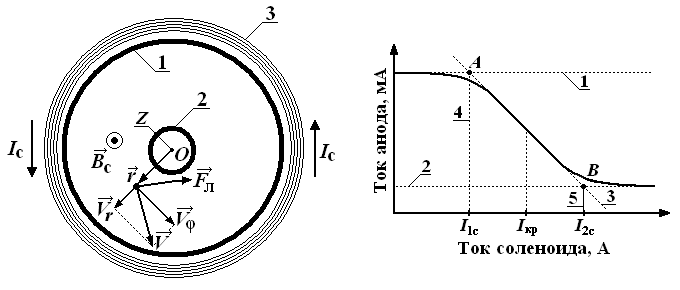 Рис. 5.3. Движение электрона Рис. 5.4. График зависимости в магнетроне: тока анода от тока 1 – анод; 2 – катод; 3 – обмотка соленоида Iа = f(Ic) соленоида; Ic – направление тока в обмотке соленоида Момент импульса электрона относительно центра катода Так как Момент силы Лоренца относительно центра катода Момент силы Лоренца относительно оси Z Так как  . (5.6) . (5.6)Из выражения (5.6) получим Если 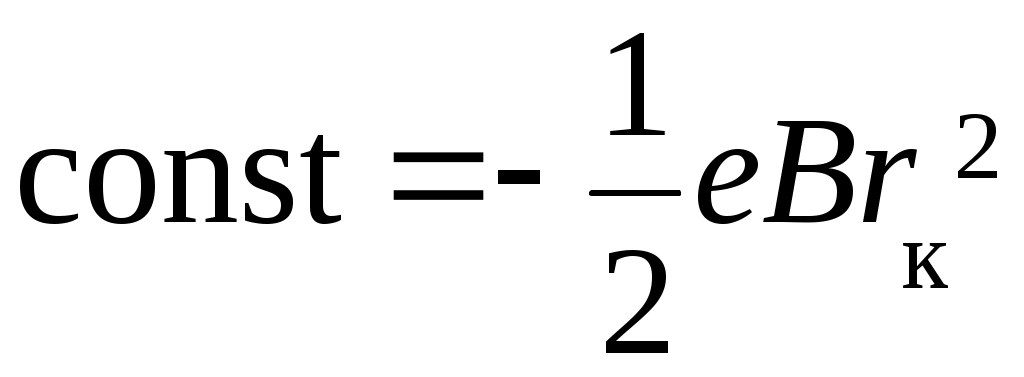 . Тогда . Тогда Кинетическая энергия электрона: 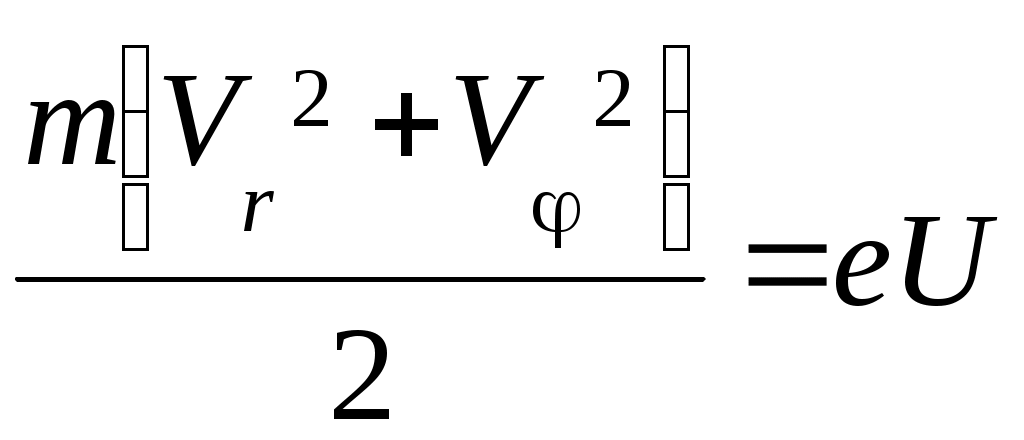 . (5.9) . (5.9)При определённом значении индукции магнитного поля, которое назовём критическим (Вкр), движение электрона становится круговым, а скорость электрона вблизи катода (r Подставляя в (5.9) значение Vφ из (5.8), получаем 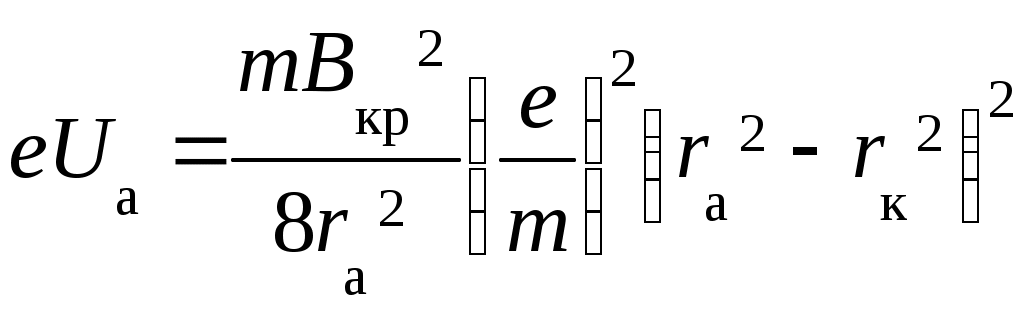 , (5.10) , (5.10)где Из (5.10) выражаем удельный заряд электрона 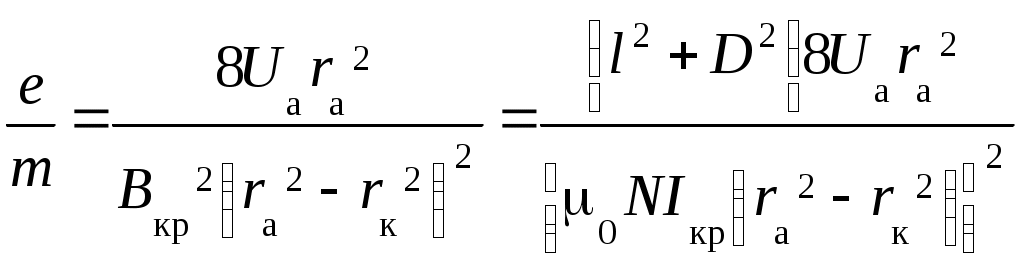 , (5.11) , (5.11)где 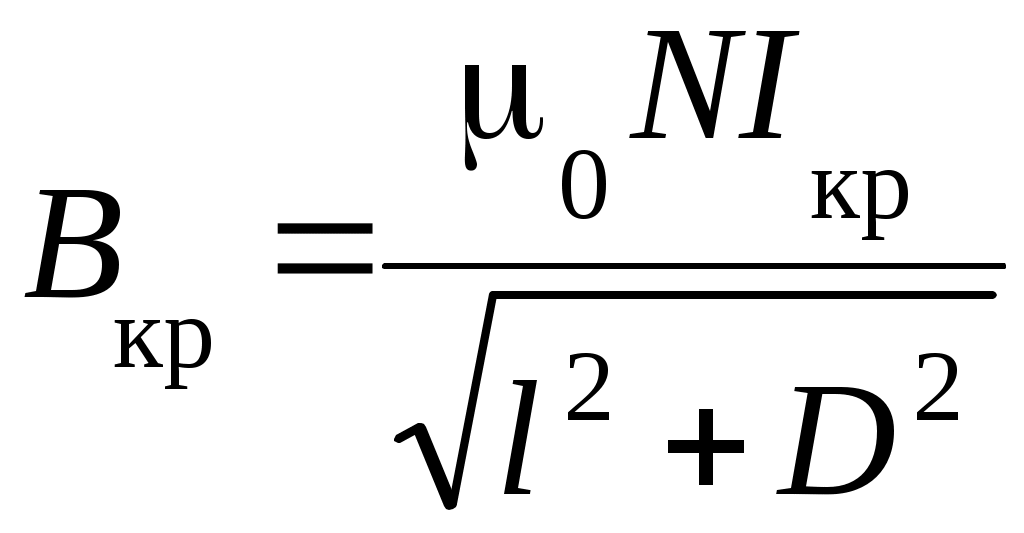 ; ; Для определения критического значения тока в соленоиде Iкр необходимо построить график зависимости Iа = f(Ic) (рис. 5.4). Линия 1 проходит через максимальное значение, а линия 2 – через минимальное значение анодного тока. Линия 3 проходит через наклонный участок графика. Из точек пересечения линий 1–3 (точка А) и 2–3 (точка В) опускаем перпендикуляры 4 и 5 на ось абсцисс, и определяем значения тока соленоида I1c и I2c. Значение критического токаIкр определяется по формуле 3.3. Определение удельного заряда электрона 3.3.1. Собрать цепь по схеме, изображённой на рис. 5.1. 3.3.2. Установить анодное напряжение Uа (от 50 до 120 В) по вольтметру V на блоке питания ИП. 3.3.3. Изменяя величину тока в соленоиде от минимального значения до максимального через 0,05 А при постоянном анодном напряжении (от 50 до 120 В), снять зависимость Iа = f(Ic). 3.3.4. Повторить все измерения при двух других значениях анодного напряжения (от 50 до 120 В). Результаты измерений занести в табл. 5.1. 3.3.5. Для каждого значения анодного напряжения построить график зависимости Iа = f(Ic). По графику определить I1с и I2с. 3.3.6. По формуле (5.12) определить Iкр. 3.3.7. По формуле (5.11) для каждого значения Iкр определить удельный заряд электрона 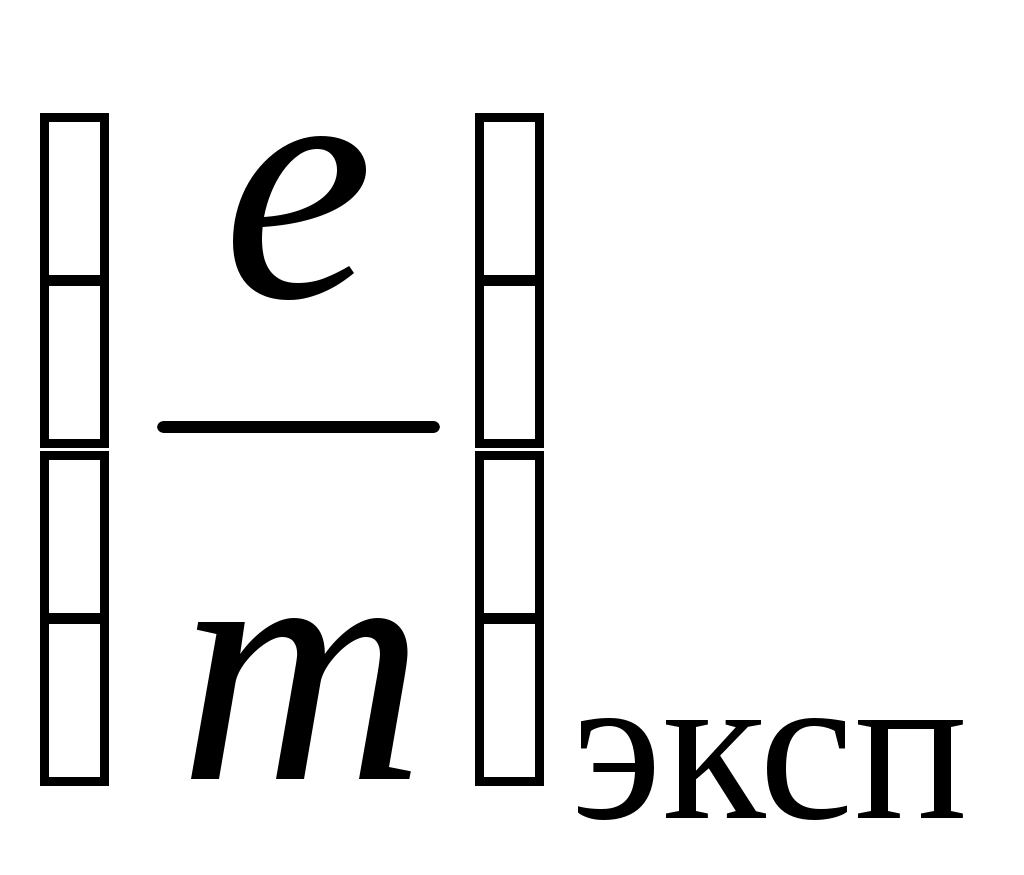 . Данные для расчёта: N = 2700; l = 0,17 м; D = 8,5 ∙ 10–2 м; rк = 1,5 ∙ 10–3 м; rа = 4 ∙ 10–3 м. . Данные для расчёта: N = 2700; l = 0,17 м; D = 8,5 ∙ 10–2 м; rк = 1,5 ∙ 10–3 м; rа = 4 ∙ 10–3 м.3.3.8. Определить среднее значение удельного заряда электрона 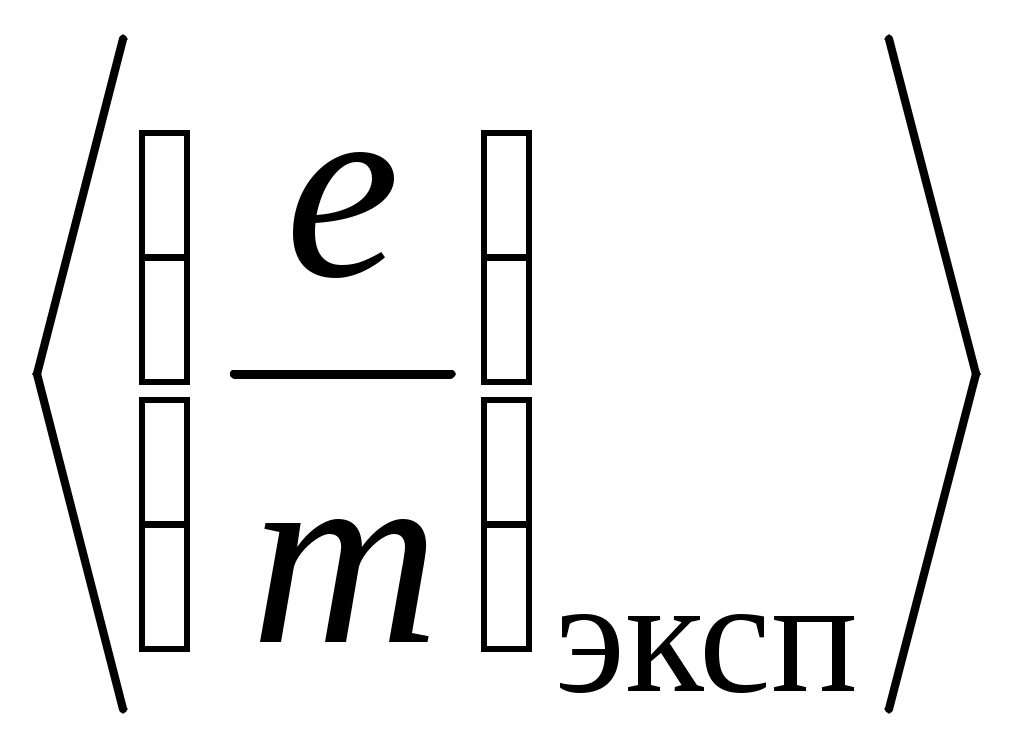 . Результаты вычислений занести в табл. 5.2. . Результаты вычислений занести в табл. 5.2.3.3.9. Определить отклонение полученного среднего значения удельного заряда от теоретического значения по формуле: 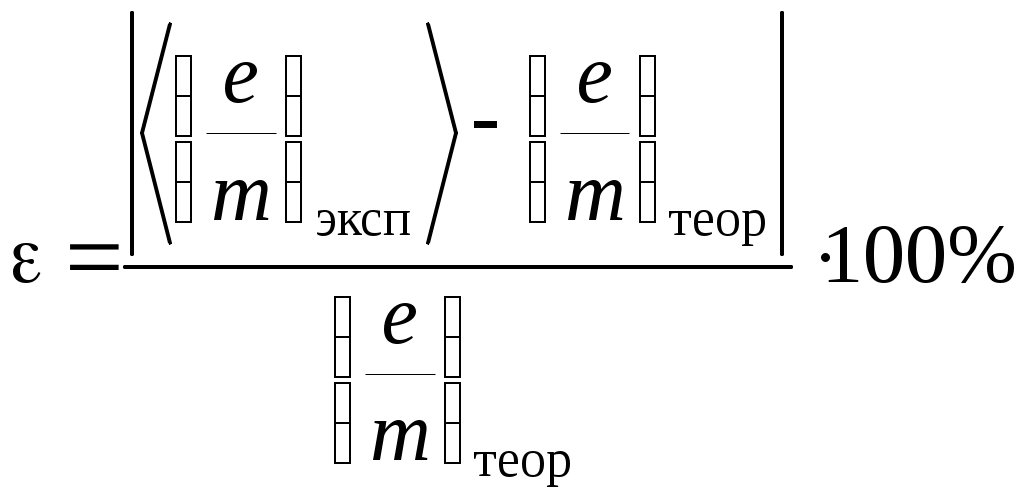 , где , где 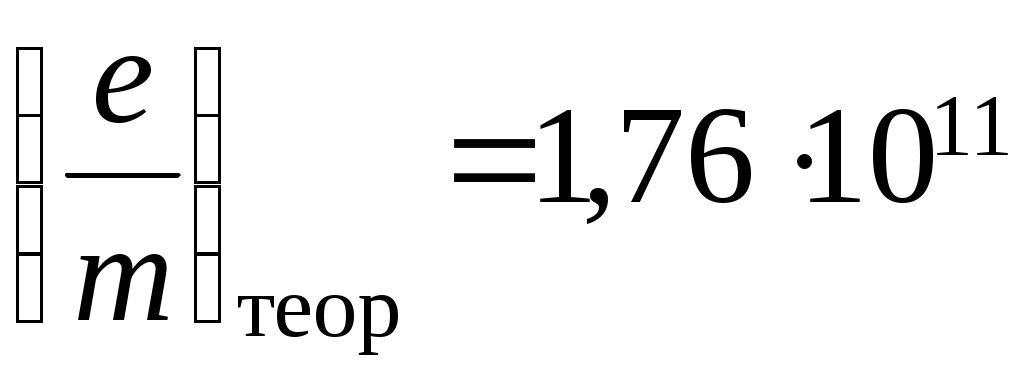 Кл/кг. Кл/кг.Таблица 5.1 Результаты измерения тока анода Ia при различных значениях анодного напряжения Ua и тока в соленоиде Iс
Таблица 5.2 Результаты определения тока Iкр, магнитной индукции Вкр и удельного заряда электрона
4. Вопросы для самоподготовки 4.1. В чём проявляется действие силы Лоренца на движущиеся электроны? 4.2. Влияет ли сила Лоренца на кинетическую энергию движущихся электрических зарядов? 4.3. В чём заключается методика определения отношения e/m? 4.4. В чём состоят достоинства и недостатки метода магнетрона? 4.5. Зависит ли отношение e/m от величины Uа? 4.6. Что изменится, если направление тока в соленоиде изменить на противоположное? 4.7. Какие электроны отклоняются на больший угол в одном и том же магнитном поле: быстрые или медленные? VI. Лабораторная работа № 6ИЗУЧЕНИЕ МАГНИТНОГО ПОЛЯ СОЛЕНОИДА С ПОМОЩЬЮ ДАТЧИКА ХОЛЛА 1. Цель работы: определение индукции магнитного поля соленоида с помощью датчика Холла. 2. Подготовка к работе: прочитать в учебниках параграфы [1] §§ 22.1, 22.2, 23.2; [2] §§ 110, 117; [3] §§ 194, 217. Для выполнения работы студент должен знать: а) закон Био – Савара – Лапласа и его применение к расчёту индукции магнитного поля соленоида; б) сущность эффекта Холла; в) методику определения индукции магнитного поля на оси соленоида с помощью датчика Холла; г) принцип действия приборов, используемых в данной лабораторной установке; д) расчёт индукции магнитного поля на оси соленоида. 3. Выполнение работы 3.1. Описание лабораторного стенда На рис. 6.1 приведена блок-схема, а на рис. 6.2 – принципиальная электрическая схема соединения элементов лабораторной установки, состоящая из модуля ФПЭ-04, источника питания ИП и цифрового вольтметра РV. Модуль ФПЭ-04 содержит в себе соленоид L и датчик Холла ДХ. Датчик располагается на торце специального штока Ш, вставляемого в соленоид. Для измерения положения датчика внутри соленоида на боковой грани штока нанесена миллиметровая шкала. 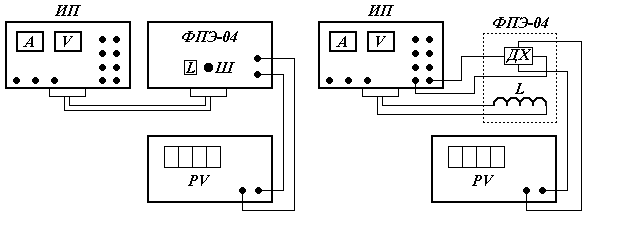 Рис. 6.1. Блок-схема установки Рис. 6.2. Принципиальная электрическая Рис. 6.1. Блок-схема установки Рис. 6.2. Принципиальная электрическаясхема соединения элементов 3.2. Методика измерений и расчёта Для исследования индукции магнитного поля на оси соленоида в данной работе используется эффект Холла, который заключается в следующем. Если через проводящую пластинку с поперечным сечением S = ah пропустить ток I плотностью Возникающая при этом разность потенциалов UX пропорциональна величине плотности тока и индукции магнитного поля где RX – постоянная Холла, [RX] = [м3/Кл]; a – ширина проводящей пластинки. Следовательно, индукция магнитного поля на оси соленоида равна:  , (6.2) , (6.2)где А – коэффициент пропорциональности между разностью потенциалов, обусловленной эффектом Холла, и индукцией магнитного поля. В работе используется полупроводниковый датчик Холла марки Х501, для которого А = 23 мТл/В с рабочим током 10 мА. 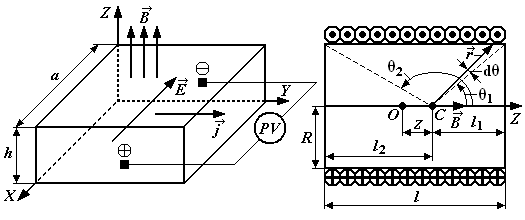 Рис. 6.3. Схема, поясняющая Рис. 6.4. Схема к расчёту индукции Рис. 6.3. Схема, поясняющая Рис. 6.4. Схема к расчёту индукцииэффект Холла магнитного поля соленоида При отсутствии магнитного поля разность потенциаловUX, обусловленная эффектом Холла, должна быть равна нулю. Однако вследствие неэквипотенциальности выходных электродов на гранях датчика вольтметр может показать некоторую разность потенциалов UX0. В данной работе эта величина равна 78 мВ. На рис. 6.4 приведена схема к расчёту индукции магнитного поля соленоида. Согласно закону Био – Савара – Лапласа индукция магнитного поля соленоида в точке С на оси Z равна 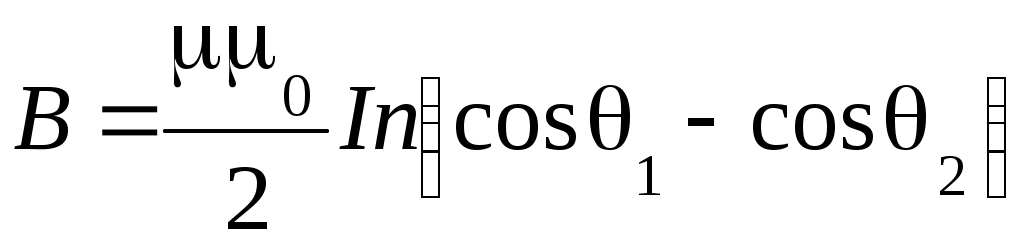 , (6.3) , (6.3)где μ– магнитная проницаемость среды; μ0 = 4π ∙ 10–7 Гн/м – магнитная постоянная; I – сила тока в витках соленоида; n – число витков соленоида на единицу длины. Из рис. 6.4 следует:  ; (6.4) ; (6.4)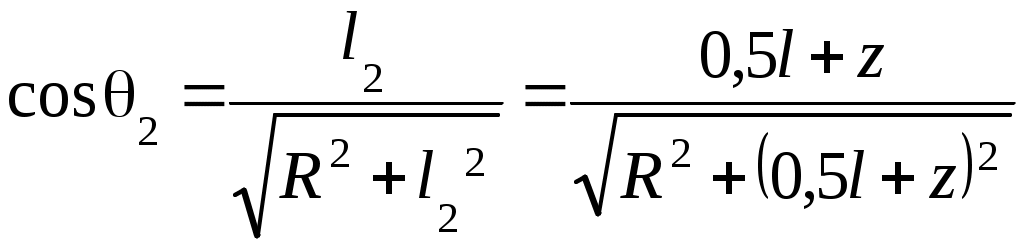 , (6.5) , (6.5)где R – радиус витков соленоида; l – длина соленоида; z – координата, отсчитываемая от центра соленоида. Если индукция магнитного поля определяется в центре соленоида (z = 0), то 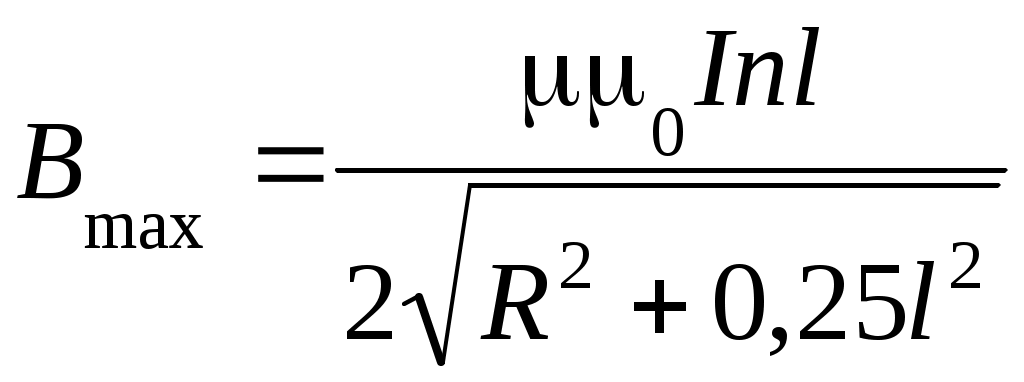 . (6.6) . (6.6)В центре бесконечно длинного соленоида (l >> R) θ1 = 0, θ2 = π: Параметры соленоида: l = 0,2 м; R = 0,02 м; n = 2700 м–1; μ = 1. 3.3. Определение зависимости магнитной индукции в средней точке на оси соленоида от тока соленоида 3.3.1. Собрать цепь по схеме, изображённой на рис. 6.1. 3.3.2. Поставить шток с датчиком Холла в среднее положение на оси соленоида («0» по шкале). 3.3.3. Включить источник питания и цифровой вольтметр в сеть 220 В. Измерить разность потенциалов UX при положении датчика в центре соленоида для тока соленоида в пределах от 0,5 до 1,6 А. Данные занести в табл. 6.1. 3.3.4. Вычислить экспериментальное значение индукции магнитного поля Вэксп для заданных значений силы тока I по формуле (6.2). Данные занести в табл. 6.1. 3.3.5. Вычислить индукцию магнитного поля бесконечно длинного соленоида В для заданных значений силы тока I по фор-муле (6.7). Данные занести в табл. 6.1. 3.3.6. Вычислить индукцию магнитного поля в центре соленоида Вmax для заданных значений силы тока I по формуле (6.6). Данные занести в табл. 6.1. 3.3.7. Построить график зависимости UX= f(I). По графику определить разность потенциалов UX0, существующую даже при отсутствии магнитного поля (I = 0). 3.3.8. Построить графики зависимостей магнитной индукции от силы тока: Bэксп = f(I); B = f(I);Bmax = f(I). Сделать выводы. Таблица 6.1 Результаты измерения разности потенциалов UX в центре соленоида при различных значениях тока в соленоиде
3.4. Исследование распределения индукции магнитного поля вдоль оси соленоида (z отсчитывается от средней точки) 3.4.1. Установить величину тока в катушке соленоида по указанию преподавателя в пределах от 1 до 2 А. 3.4.2. Перемещая шток с датчиком Холла вдоль оси соленоида с интервалом Δz = 10 мм, измерить UX. 3.4.3. Вычислить индукцию магнитного поля Bэксп для каждого положения датчика Холла по формуле (6.2). 3.4.4. По формулам (6.4) и (6.5) рассчитать cosθ1 и cosθ2. Рассчитать индукцию магнитного поля Врасч для каждого положения датчика Холла по формуле (6.3). Полученные результаты занести в табл. 6.2. 3.4.5. Рассчитать относительное расхождение результатов по формуле: 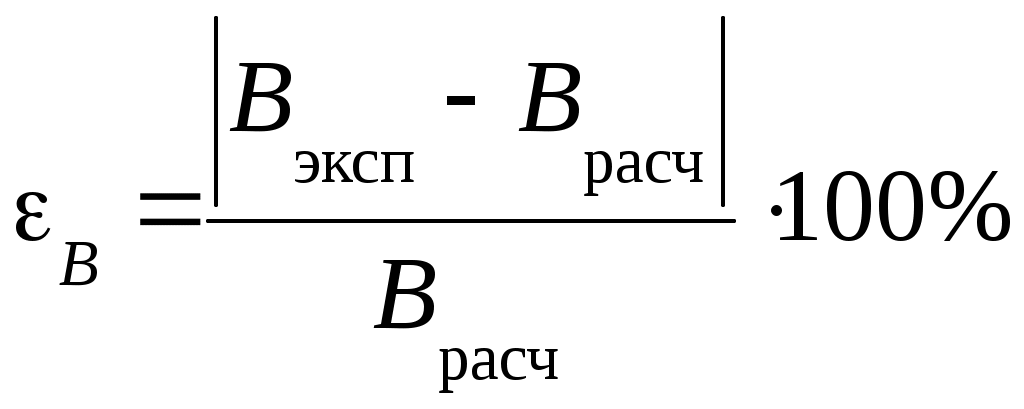 . .3.4.6. Построить график зависимости Вэксп= f(z). Таблица 6.2 Результаты измерения разности потенциалов UX на оси соленоида
4. Вопросы для самоподготовки 4.1. Как применить закон Био – Савара – Лапласа для расчёта индукции магнитного поля на оси соленоида? 4.2. Как определить индукцию магнитного поля бесконечно длинного соленоида? 4.3. В чём заключается эффект Холла? 4.4. Почему ЭДС Холла в металлах и полупроводниках раз-лична? 4.5. Как уменьшить неэквипотенциальность электродов, изме-ряющих разность потенциалов UX? 4.6. Какие ещё существуют методы измерения индукции магнитного поля? Охарактеризовать достоинства и недостатки. 4.7. Как рассчитать магнитную индукцию движущегося заряда? 4.8. От каких параметров зависит постоянная Холла? VII. Лабораторная работа № 7ИССЛЕДОВАНИЕ СВОЙСТВ ФЕРРОМАГНЕТИКОВ 1. Цель работы: исследование зависимости магнитной проницаемости ферромагнетика от напряжённости магнитного поля и определение потерь на гистерезис. 2. Подготовка к работе: прочитать в учебниках параграфы [1] §§ 24.5, 25.4; [2] §§ 129, 130, 135, 136; [3] §§ 203, 204, 228, 229. Для выполнения работы студент должен знать: а) природу ферро-магнетизма и свойства ферромагнетиков; б) явление магнитного гистерезиса; в) метод определения напряжённости и индукции магнитного поля; г) калибровку осей осциллографа; д) метод графического дифференцирования; е) метод определения потерь на перемагничивание ферромагнетика; ж) порядок настройки приборов, используемых в данной лабораторной установке. 3. Выполнение работы 3.1. Описание лабораторного стенда На рис. 7.1 приведена принципиальная электрическая схема лабораторной установки, состоящая из трансформатора напряжения ТР с ферромагнитным сердечником, ЛАТРа Л, сопротивлений R1 и R2, конденсатора С, ключа К, вольтметра V, амперметра А и электронного осциллографа ЭО. На горизонтально отклоняющие пластины X электронного осциллографа ЭО подаётся напряжение UX с сопротивления R1, пропорциональное напряжённости магнитного поля H в сердечнике трансформатора ТР. На вертикально отклоняющие пластины Y подаётся напряжение UY с конденсатора С, пропорциональное индукции магнитного поля В в сердечнике трансформатора ТР. В результате на экране осциллографа ЭО появляется петля гистерезиса (кривая 1 на рис. 7.2). За один период изменения силы тока след электронного луча на экране описывает полную петлю гистерезиса, а за следующий период в точности повторяет её. Поэтому на экране будет видна неподвижная петля гистерезиса. Изменяя с помощью ЛАТРа Л напряжение UX, можно получить на экране ряд различных по своей площади петель гистерезиса (кривые 2и3 на рис. 7.2). 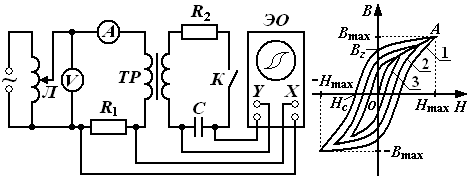 Рис. 7.1. Принципиальная электрическая Рис. 7.2. Зависимость Рис. 7.1. Принципиальная электрическая Рис. 7.2. Зависимостьсхема лабораторной установки магнитной индукции В от напряжённости намагничивающего поля Н для ферромагнетика На рис. 7.2 кривая ОА является основной кривой намагниче-ния; Вг – остаточная намагниченность; Нс – коэрцитивная сила; Hmax и Bmax – координаты КХ и КY вершин петли гистерезиса. 3.2. Методика измерений и расчёта 3.2.1. Метод определения напряжённости и индукции магнитного поля ферромагнитного сердечника Напряжение UX, подаваемое с сопротивления R1 на вход Х осциллографа, равно где I1 – действующее значение силы тока в первичной обмотке трансформатора, измеряемое амперметром А. Токв первичной обмотке создаёт в сердечнике трансформатора магнитное поле напряжённостью 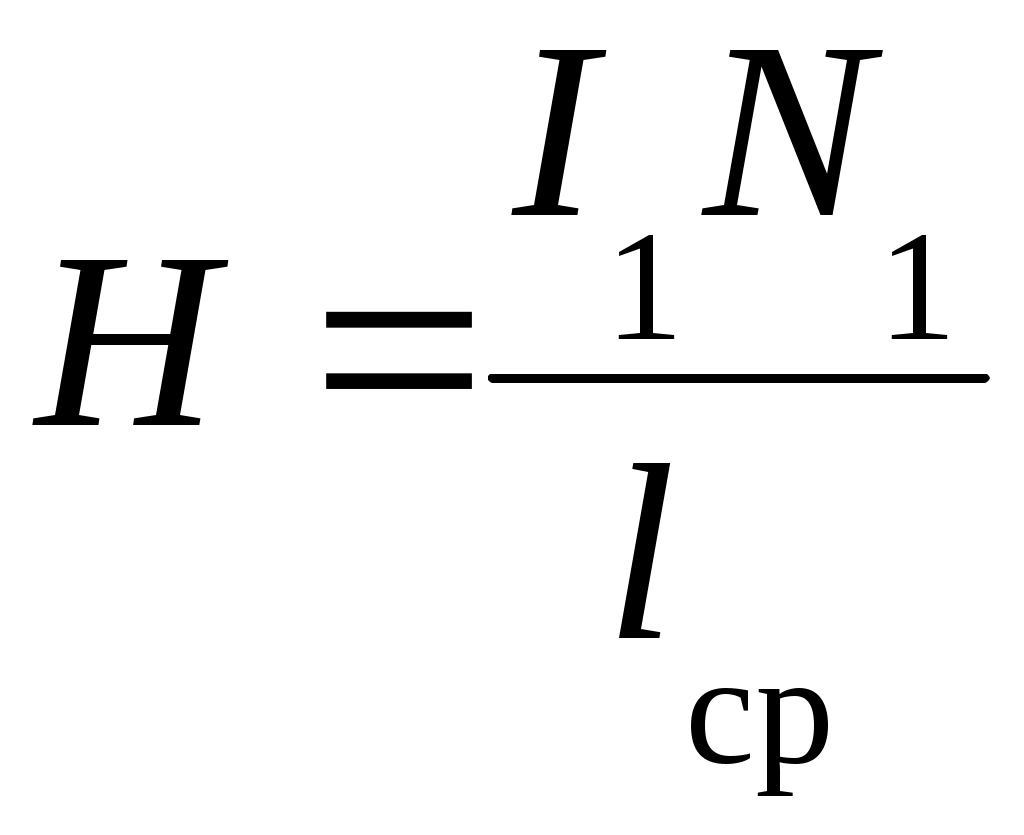 , (7.2) , (7.2)где N1 – число витков первичной обмотки трансформатора; lср – длина средней линии сердечника. Выразив значениеI1 из (7.2) и подставив его в (7.1), получим 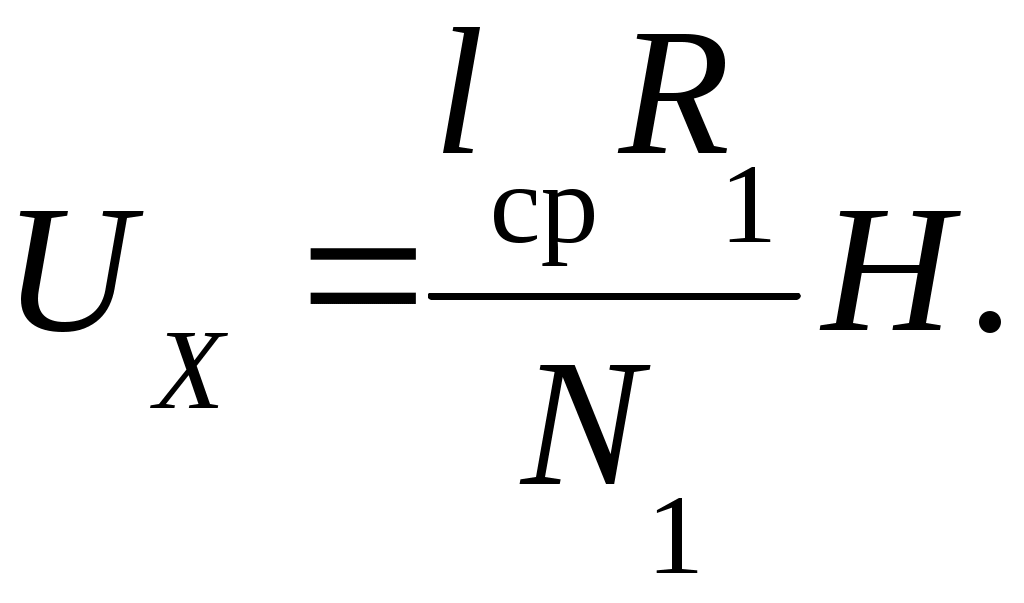 (7.3) (7.3)ЭДС, наводимая во вторичной обмотке трансформатора переменным магнитным потоком, равна где Согласно второму правилу Кирхгофа для мгновенных значений можно записать Так как 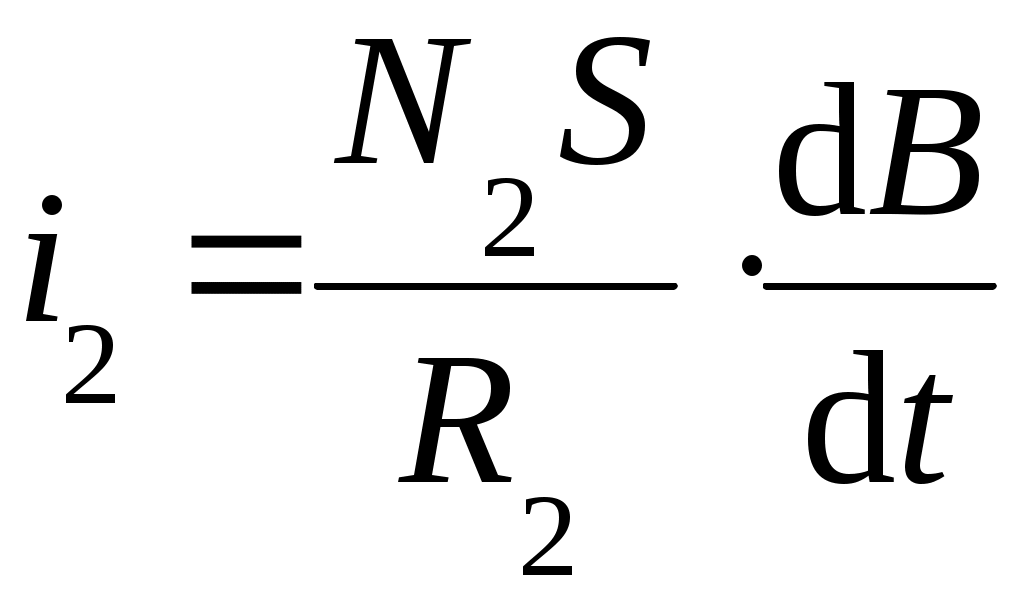 . (7.6) . (7.6)Напряжение UY, подаваемое с конденсатора С на вход Y осциллографа, равно Из формул (7.3) и (7.7) выражаем H и B: 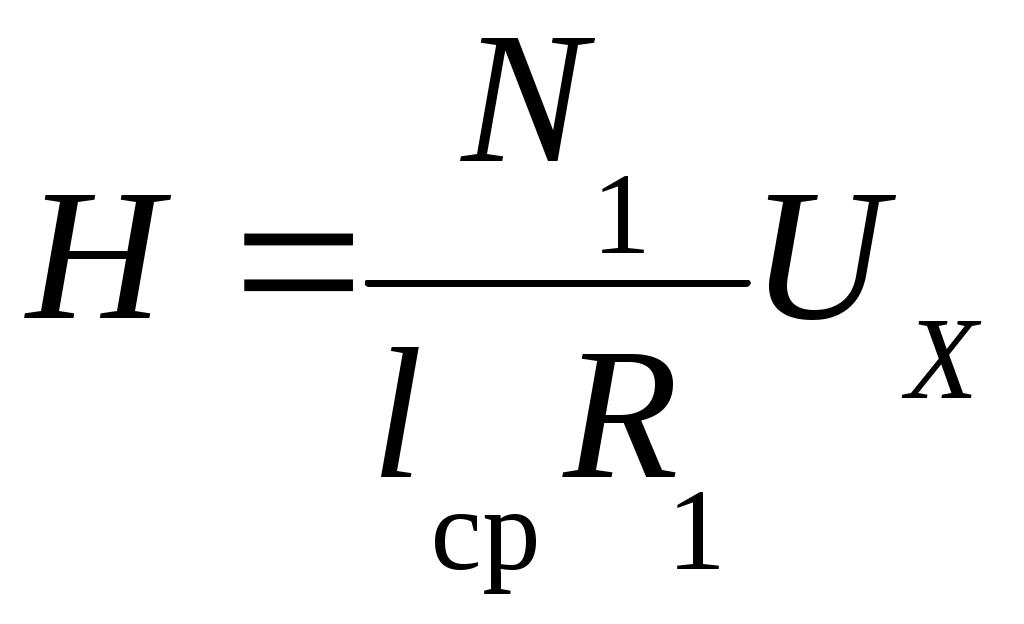 ; ; 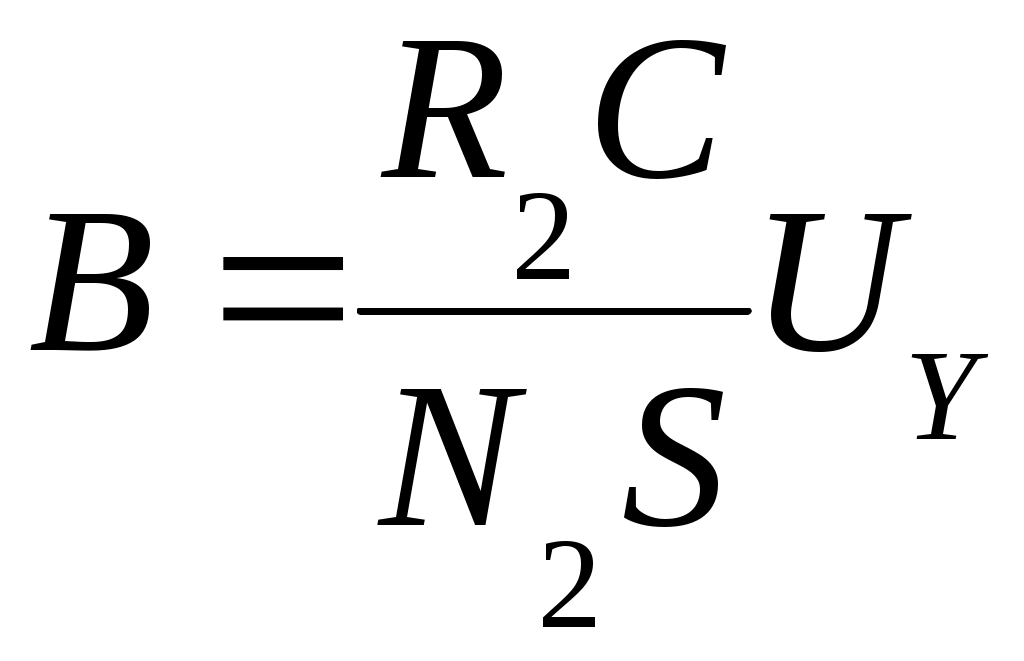 . (7.8) . (7.8)3.2.2. Калибровка осей осциллографа Для определения напряжений Выбор усиления по осям осциллографа производится следу-ющим образом. С помощью рукояток «усиление по горизонтали», «усиление по вертикали» и ЛАТРа добиться, чтобы петля гистерезиса имела участок насыщения и занимала большую часть экрана. После этого на вход горизонтально и вертикально отклоняющих пластин осциллографа подать по очереди определённое напряжение с выхода ЛАТРа, измеренное вольтметром. Одновременно нужно измерить в делениях шкалы осциллографа соответствующие полные отклонения луча по осям. Тогда масштабы по осям X и Y определятся из выражений:  ; ; 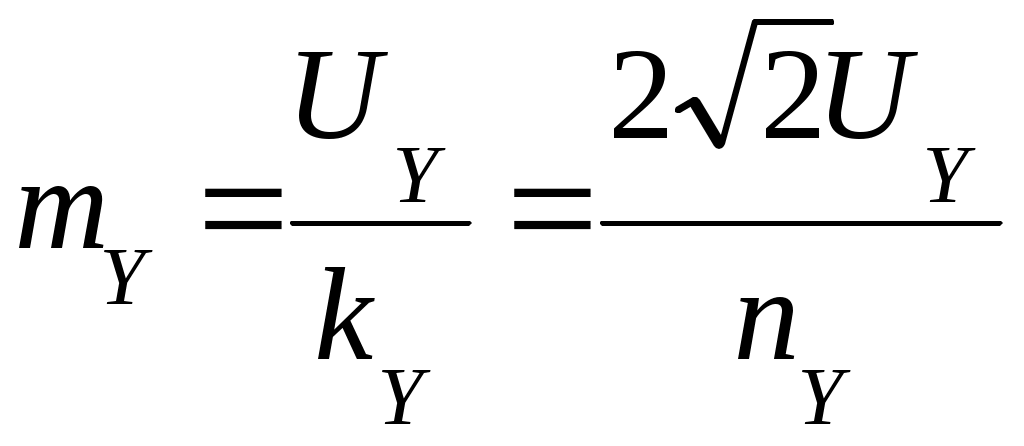 , (7.9) , (7.9)где Задавая несколько значений напряжений Выразив из (7.9) значения  ; (7.10) ; (7.10)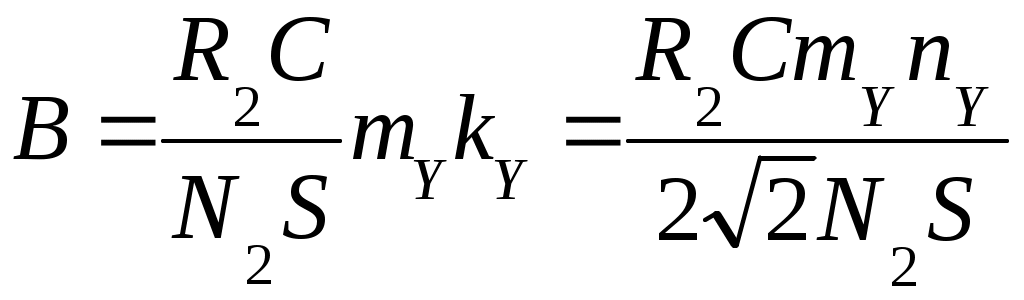 . (7.11) . (7.11)3.2.3. Определение магнитной проницаемости методом графического дифференцирования Статическая где Динамическую магнитную проницаемость 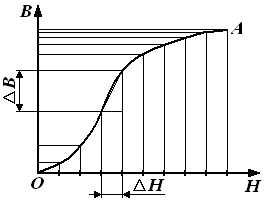 Рис. 7.3. Разбиение основной кривой намагничения на интервалы методом графического дифференцирования 3.2.4. Определение потерь на перемагничивание (гистерезис) При перемагничивании ферромагнитного сердечника часть энергии, потребляемой из сети, затрачивается на переориентировку доменов и возбуждение вихревых токов, и в конечном счёте, переходит в тепловую энергию. Изменение объёмной плотности энергии магнитного поля при изменении напряжённости поля на величину dH равно Из (7.13) следует, что энергия магнитного поля, затрачиваемая на перемагничивание единицы объёма ферромагнетика за один период изменения силы тока равна площади петли гистерезиса S, выраженной в соответствующих единицах: Если цена деления масштабной шкалы осциллографа в направлении оси H равна Потери при перемагничивании всего ферромагнетика за один период изменения силы тока определяются по формуле где 3.3. Снятие основной кривой намагничения 3.3.1. Собрать цепь по схеме, изображённой на рис. 7.1. 3.3.2. Выбрать соответствующие усиления по горизонтальной и вертикальной осям осциллографа. Изменяя с помощью ЛАТРа напряжение на входе установки, получить на экране осциллографа семейство петель гистерезиса. Для каждой из них измерить координаты вершин КХ и КY. Опыт повторить не менее 10 раз. Результаты занести в табл. 7.1. 3.3.3. Произвести калибровку осей осциллографа. Измерения произвести для 5–6 значений в диапазоне напряжений, используемых для снятия основной кривой намагничения. 3.3.4. По формулам (7.9) вычислить масштабы 3.3.5. Вычислить значения напряжённости магнитного поля Н и индукции магнитного поля В по формулам (7.10) и (7.11). Значения занести в табл. 7.1. 3.3.6. По данным табл. 7.1 построить основную кривую намагничения. 3.4. Исследование зависимости магнитной проницаемости от напряжённости магнитного поля 3.4.1. По формуле (7.12) вычислить статическую магнитную проницаемость 3.4.2. Используя метод графического дифференцирования, по формуле (7.12) найти динамическую магнитную проницаемость 3.4.3. По данным табл. 7.1 построить графики зависимостей 3.5. Определение потерь на гистерезис 3.5.1. Зарисовать предельную петлю гистерезиса в делениях координатной сетки осциллографа и подсчитать число клеток М, которые содержит петля. 3.5.2. Рассчитать потери на гистерезис для единицы объёма ферромагнитного сердечника по формуле (7.15). 3.5.3. Рассчитать потери на гистерезис для всего ферромагнитного сердечника по формуле (7.16). Таблица 7.1 Результаты определения статической и динамической проницаемостей ферромагнитного сердечника
Таблица 7.2 Результаты калибровки осей осцилографа и определения потерь на гистерезис
4. Вопросы для самоподготовки 4.1. В чём состоит природа ферромагнетизма? Что называют доменом? 4.2. Почему зависимость 4.3. В чём заключается отличие динамической магнитной проницаемости от статической? 4.4. Как изменится основная кривая намагничения, если сер-дечник будет иметь воздушный зазор? 4.5. Почему сердечники различных устройств набирают из отдельных листов, изолированных друг от друга? 4.6. Какую форму имеет ток и напряжение в цепи, содержа-щий катушку с ферромагнитным сердечником? 4.7. Какими преимуществами обладает ферритовый сердеч-ник? 4.8. В чём заключается явление магнитострикции? 4.9. В чём проявляется эффект Виллари? 4.10. Что такое точка Кюри? VIII. Список рекомендуемой литературы 1. Детлаф, А. А. Курс физики : учеб. пособие для студентов втузов / А. А. Детлаф, Б. М. Яворский. – 4-е изд., испр. – М. : Ака-демия, 2007. – 720 с. 2. Трофимова, Т. И. Курс физики : учеб. пособие для инж.-техн. специальностей вузов / Т. И. Трофимова. – 14-е изд., стерео-тип. – М. : Академия, 2007. – 560 с. 3. Фриш, С. Э.; Тиморева, А. В. Курс общей физики : учеб. пособие : в 3 т. Т. 2 : Электрические и электромагнитные явления / С. Э. Фриш, А. В. Тиморева. – 11-е изд., стереотип. – СПб. : Лань, 2007. – 528 с.  Составитель Александр Витальевич Десятниченко ЭЛЕКТРОМАГНЕТИЗМ Лабораторный комплекс К-315.1 Методические указания для подготовки к выполнению лабораторныхработ по курсу физики для студентов технических специальностей Рецензент В. В. Дырдин Печатается в авторской редакцииПодписано в печать Формат 60 Бумага офсетная. Отпечатано на ризографе. Уч.-изд. л. 2,6. Тираж экз. Заказ ГУ КузГТУ. 650000, Кемерово, ул. Весенняя, 28. Типография ГУ КузГТУ. 650000, Кемерово, ул. Д. Бедного, 4А. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

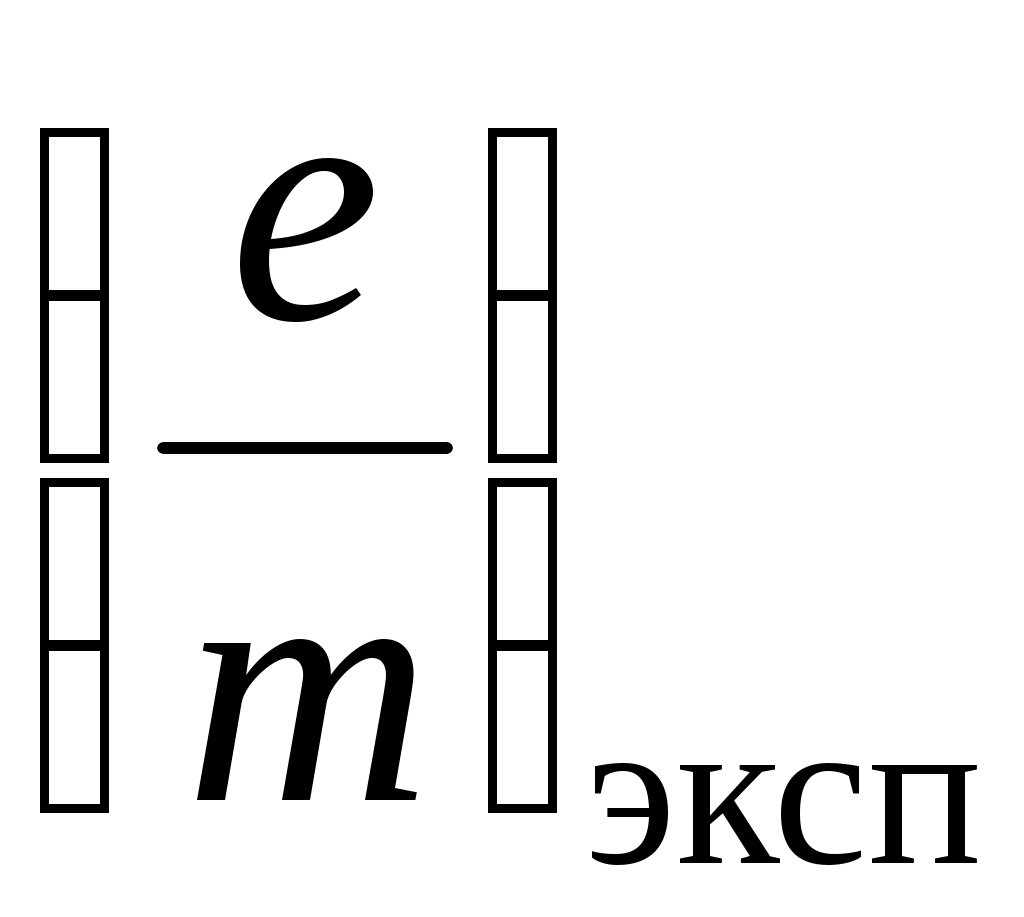 , Кл/кг
, Кл/кг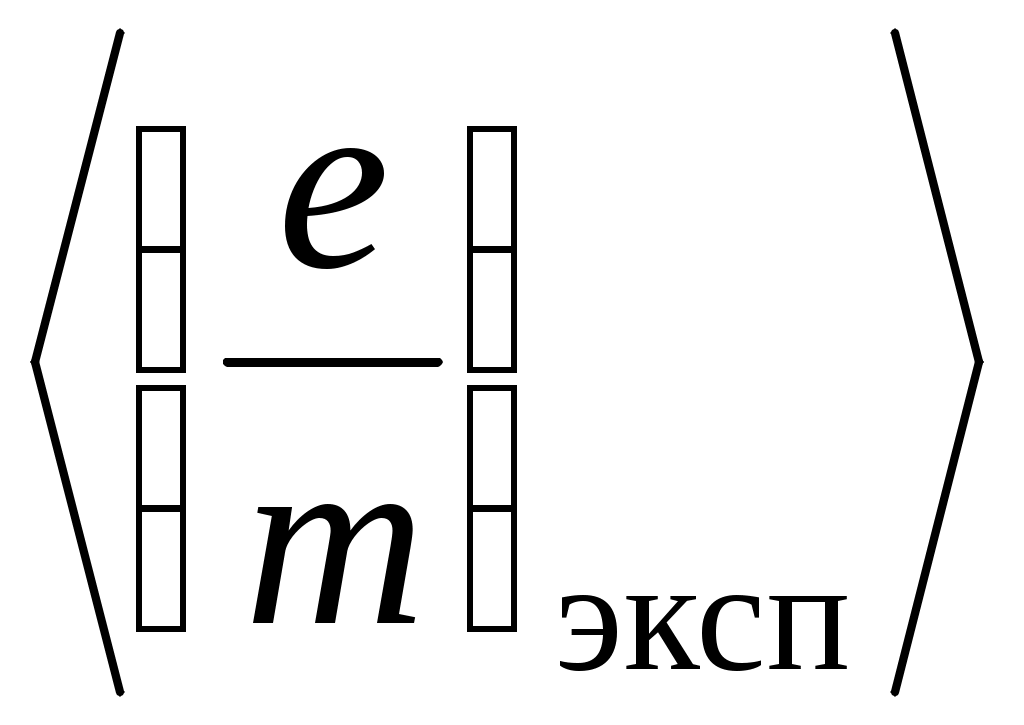 , Кл/кг
, Кл/кг