Основы. Основы НИ. ПР №1. Методические указания для выполнения практической работы по курсу Методология научных исследований в технологии
 Скачать 383.5 Kb. Скачать 383.5 Kb.
|
|
Продолжение таблицы 2.
Таблица 3. Результаты эксперимента по исследованию влияния подачи s на величину неровностей Rz при точении стали 4Х10С2М
Таблица 4. Результаты эксперимента исследования влияния на стойкость T сверл толщины h их сердцевины
Таблица 5. Результаты исследования зависимости температуры резания θ при точении стали 40Х резцом с пластинкой из твердого сплава Т60К6 от скорости обработки v
Таблица 6. Результаты эксперимента исследования влияния на стойкость T сверл обратной конусности x
Таблица 7. Результаты исследования зависимости отношения радиальной и тангенциальной сил резания Py/Pz от глубины резания t при шлифовании деталей из твердого сплава Т30К4
Таблица 8. Результаты исследования зависимости температуры θ в зоне контакта от времени шлифования τ стали 40Х3СМВФЮ
Таблица 9. Результаты исследования зависимости температуры θ в зоне контакта от скорости резания v при ленточном шлифовании титанового сплава ВТ8
Таблица 10. Результаты исследования влияния силы P прижатия инструмента к обрабатываемой поверхности на величину неровностей Rа при алмазном выглаживании закаленной стали 45
Таблица 11. Результаты исследования влияния силы выглаживания P на твердость HV поверхности деталей из закаленной стали 45
Таблица 12. Результаты исследования влияния исходной шероховатости Rа исх на шероховатость Rа обработанной поверхности при обкатывании отожженной стали 45
Порядок выполнения работы Ознакомьтесь с теоретическими основами корреляционного и регрессионного анализов, применяемых при исследовании связей между факторами и параметрами объекта. Составьте задание с конкретизацией задачи (какой процесс исследуется, какой его параметр и фактор изучаются, что следует установить). Выполните корреляционный анализ данных эксперимента о наличии или отсутствии связи между исследуемыми характеристиками процесса с помощью электронной таблицы Excel, используя ее функцию «Корреляция»1. Для этого откройте Office Excel и занесите в открывшейся книге Excel по столбцам, начиная с ячеек A2 и B2, результаты эксперимента из таблицы задания. В ячейках A1 и B1 укажите наименования соответствующих столбцов (рисунок 1). В массив ячеек D1:E31 скопируйте данные ячеек A1:B31 и удалите содержимое ячейки D1. Результаты этой операции позволят в дальнейшем выполнить построение графиков исследуемого параметра с помощью «Мастера диаграмм» Excel. В меню Microsoft Excel выберите «Сервис» и обратитесь к команде «Анализ данных»1. В меню «Инструменты анализа» выделите «Корреляция» и в появившемся окне заполните требуемые данные для вычисления коэффициента корреляции и укажите адрес ячейки вывода результатов (например, F2 на рис. 1). По выведенному значению коэффициента корреляции сделайте предварительный вывод о наличии и форме связи между исследуемым параметром и фактором процесса режима обработки. Выявите графическим методом вид уравнения регрессии, описывающего связь исследуемого параметра с фактором режима обработки. Для этого последовательно постройте с помощью «Мастера диаграмм» пакета Excel точечные графики данных массива ячеек D1:E31 с отображением на них линии тренда (линейной, полиномиальной и др.). Визуально по линии регрессии и характеру разброса экспериментальных данных относительно этой линии определите наиболее подходящий вид уравнения регрессии. Сформулируйте выводы по полученным результатам исследований. Составьте отчет. 4. Содержание отчета Название темы практической работы. Задание с таблицей результатов эксперимента. Результаты корреляционного анализа данных эксперимента о наличии или отсутствии связи между исследуемыми характеристиками процесса, полученные с помощью Excel. Предварительный вывод о наличии и форме связи между исследуемым параметром и фактором процесса режима обработки. Графики экспериментальных данных с отображением на них линии тренда (линейной, полиномиальной и др.). Результаты выбора наиболее подходящего вида уравнения регрессии, отражающего взаимосвязь между исследуемыми характеристиками процесса. Выводы. 5. Пример оформления отчета Тема. Исследование связей между параметрами и факторами объекта 5.1. Задание При исследовании влияния подачи s на высоту неровностей Rz при точении стали 4Х10С2М получены опытные данные, приведенные в таблице 13. Таблица 13. Результаты эксперимента по исследованию влияния подачи s на величину неровностей Rz при точении стали 4Х10С2М
Установить наличие связи между подачей и высотой неровностей, силу и форму этой связи. Проверить достоверность рабочей гипотезы о наличии связи между высотой неровностей Rz и подачей s в виде квадратичной зависимости 5.2. Результаты выполнения задания Решение вопроса о наличии или отсутствии связи между подачей и высотой неровностей выполним с помощью электронной таблицы Excel. Занесем данные табл. 13 в ячейки A2:A31 и B2:B31 (рис. 1). В ячейках A1 и B1 укажем наименования соответствующих столбцов. Вычислим коэффициент корреляции, используя функцию Excel «Корреляция». Для этого в меню пакета Microsoft Excel выберем «Сервис», в котором обращаемся к команде «Анализ данных». В меню «Инструменты анализа» выделим «Корреляция» и в появившемся окне заполним требуемые данные для вычисления коэффициента корреляции и укажем адрес F2 ячейки вывода результатов расчета. По значению коэффициента корреляции (в ячейке G4 массива F2:H4 результатов функции «Корреляция») можно заключить, что между высотой неровностей Rz и подачей s существует достаточно тесная связь, которая может быть описана линейной зависимостью.
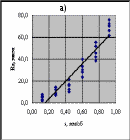
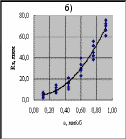
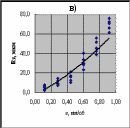
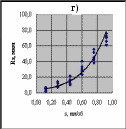
Рис.1. Результаты исследования влияния подачи s на высоту неровностейRz Для определения графическим методом вида уравнения регрессии Rz на s построим с помощью «Мастера диаграмм» пакета Excel точечные графики экспериментальных данных, используя массив ячеек D1:E31 (рис.1). Отобразим на них линии тренда: линейную (график а), полиномиальную второй степени (график б), степенную (график в) и экспоненциальную (график г). Визуальный анализ характера разброса точек экспериментальных данных и расположения относительно них линий тренда позволяет заключить, что наиболее подходящим уравнением регрессии, отражающим взаимосвязь между высотой неровностей Rz и подачей s, является полином второй степени 5.3. Выводы. На основании результатов обработки экспериментальных данных можно сделать следующие выводы. Значение коэффициента корреляции r = 0,95 указывает, что при точении стали 4Х10С2М между высотой неровностей Rz и подачей s существует достаточно тесная связь. Наиболее подходящим уравнением регрессии, отражающим взаимосвязь между высотой неровностей Rz и подачей s, является полином второй степени Контрольные вопросы В чем отличие стохастической связи между случайными величинами от функциональной? Корреляционная и стохастическая связи между случайными величинами. Что объединяет и что различает эти связи? Какие три вопроса исследуют с помощью корреляционного анализа? Что характеризует коэффициент корреляции? Какие значения он может принимать? Что оценивает корреляционное отношение? Какие значения может принимать корреляционное отношение? Какую задачу решают с помощью регрессионного анализа? Какие процедуры включает в себя регрессионный анализ? В чем сущность проверки на адекватность полученной регрессионной зависимости? ЛитератураКацев П. Г. Статистические методы исследования стойкости режущего инструмента / П. Г. Кацев. - М.: «Машиностроение», 1974. – 231 с. Солонин И. С. Математическая статистика в технологии машиностроения / И. С. Солонин. - М.: «Машиностроение», 1972. – 216 с. Основы научных исследований: Учебник для вузов / под ред. В. И. Крутова, В. В. Попова / - М.: Высшая школа.,1989. 400 с. Основы научных исследований: Учебник для вузов / под ред. В. Г. Кучерова / ВолгГТУ. Волгоград, 2004. 304 с. Пойлов В. З. Основы научных и инженерных исследований: учеб. пособие / В.З. Пойлов. – Пермь: Изд-во Перм. гос. техн. ун-та, 2008. 344 с. 1 Выполнение корреляционного и регрессионного анализов связано с определением различных статистических характеристик (средних арифметических значений, дисперсий и т. д.), вычисление которых является достаточно трудоемкими процедурами. Однако трудоемкость проведения корреляционного и регрессионного анализов значительно уменьшается при использовании функций (подпрограмм) пакета Microsoft Excel. 1 Эта функция вычисляет коэффициент корреляции между исследуемыми случайными величинами. 1 Если в меню «Сервис» Microsoft Excel нет строки «Анализ данных», то следует в меню «Сервис» загрузить «Надстройки» и напротив «Пакет анализа» поставить флажок. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||