Основы. Основы НИ. ПР №1. Методические указания для выполнения практической работы по курсу Методология научных исследований в технологии
 Скачать 383.5 Kb.
|
|
Анализ результатов предварительно проведенной небольшой серии опытов позволил выдвинуть рабочую гипотезу о том, что связь между стойкостью y и величиной заднего угла x существует и является нелинейной. Получить ответы на указанные выше вопросы и, следовательно, подтвердить или опровергнуть выдвинутую гипотезу можно с помощью таких статистических характеристик, как коэффициент корреляции и корреляционное отношение. Коэффициент корреляции является показателем того, насколько связь между случайными величинами y и x близка к строгой линейной зависимости. С точки зрения наличия связи и формы связи коэффициент корреляции в одинаковой степени характеризует и слишком большую долю случайности, и слишком большую криволинейность имеющейся связи. Учитывая эти свойства коэффициента корреляции, определение связи между случайными величинами начинают с вычисления его значения, так как даже в случае криволинейной зависимости он характеризует степень приближения корреляционной зависимости к функциональной зависимости и дает ориентировочное представление о тесноте корреляционной связи. Поскольку в исследованиях имеют дело с данными выборки из генеральной совокупности, то вычисляют выборочный коэффициент корреляции r по формуле: 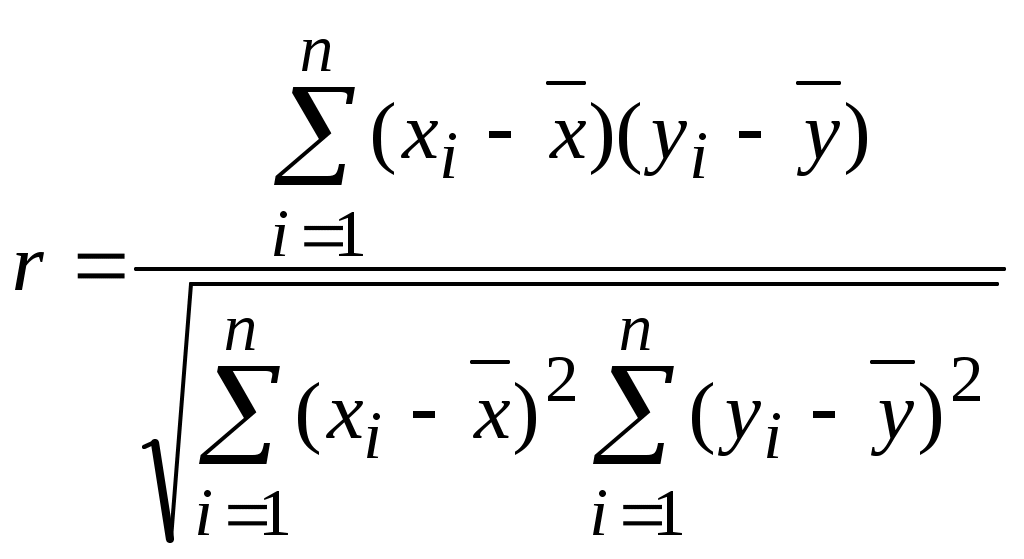 , (1)где r – коэффициент корреляции величин x и y; xi и yi - измеренные значения случайных величин, например фактора x и параметра y изучаемого объекта;  и  – средние арифметические значения величин x и y; n – число измерений (опытов).Значения r заключены между -1 и 1. Расчет по данным таблицы 1 коэффициента корреляции дает результат  , что указывает о возможности принятия выдвинутой гипотезы. Коэффициент корреляции оценивает тесноту только линейной корреляционной связи. Оценка тесноты любой корреляционной связи осуществляется с помощью корреляционного отношения.Выборочное корреляционное отношение – это отношение межгруппового среднего квадратического отклонения  к об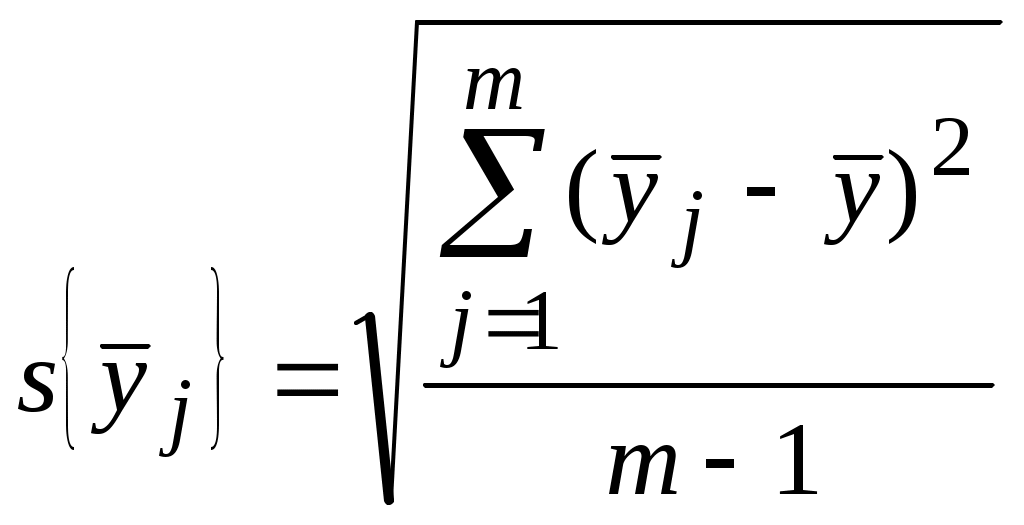щему среднему квадратическому отклонению   ,где  ;  ,в которых m – число выделенных групп результатов испытаний. Значения η заключены между 0 и 1. В частности, для приведенных данных исследования зависимости между стойкостью y и величиной заднего угла x корреляционное отношение η=0,25. Корреляционное отношение является мерой тесноты любой, в том числе и линейной, формы. Вместе с тем корреляционное отношение не позволяет судить, насколько близко расположены точки, найденные по данным наблюдений, к кривой определенного типа, например к параболе, гиперболе и т. д. Это объясняется тем, что при определении корреляционного отношения вид корреляционной зависимости между y и x во внимание не принимается. Основные свойства коэффициента корреляции и корреляционного отношения [4]. Если коэффициент корреляции r = ±1, то y и x связаны линейной связью вида y = a + bx. Если r = 0, то между y и x не может существовать прямолинейная связь, но криволинейная возможна. Чем ближе значение r к ± 1, тем точнее и теснее корреляционная прямолинейная связь между y и x. Она ослабевает с приближением r к нулю. Если корреляционное отношение η = 0, то между y и x нет корреляционной связи. Если η = 1, то y связано с x однозначной (детерминированной) связью, т. е. всякому значению x соответствует одно определенное значение y. Чем ближе η к единице, тем теснее связь y с x; чем ближе η к нулю, тем эта связь слабее. В заключение отметим, что теория корреляции позволяет: 1. Установить форму корреляционной связи, т. е. вид корреляционной зависимости между y и x (линейная или нелинейная). 2. Оценить силу (тесноту) корреляционной связи. За критерий оценки принимается величина рассеяния значений y вокруг условного среднего  . Так, если при малом рассеянии мы имеем корреляционную связь значительной силы до предела, когда y и x связаны функционально, то при большом рассеянии зависимость y от x выражена слабо, вплоть до ее полного отсутствия вообще.Регрессионный анализ. Корреляционный анализ позволяет установить отсутствие или наличие связи между факторами и исследуемым параметром объекта, силу и форму этой связи. Однако остается не выясненным вопрос, какой математической зависимостью может быть описана эта корреляционная связь. Ответ на этот вопрос дает регрессионный анализ. Задачей регрессионного анализа является установление вида эмпирических зависимостей, отражающих связи между характеристиками изучаемого объекта, и оценку адекватности построенных зависимостей. При наличии корреляционной зависимости между y и x в виде уравнения y = f (x) его принято в регрессионном анализе называть уравнением регрессии y на x, функцию f (x) – регрессией y на x. Различают однофакторную и многофакторную регрессионные зависимости. Однофакторная регрессия может быть аппроксимирована прямой линией, параболой, гиперболой, показательной функцией, полиномом и др. Если параметр y является функцией от нескольких факторов, ее графическое представление будет иметь вид n‑мерной поверхности. Проведение регрессионного анализа рассмотрим на примере однофакторного регрессионного анализа. Такой анализ имеет широкое практическое применение в технологии машиностроения. В частности, он используется при исследовании зависимости жесткости узлов станка от нагрузки, исследовании зависимостей высоты шероховатостей обработанной поверхности от какого-либо фактора режима резания, стойкости режущего инструмента, устойчивости технологического процесса во времени и т. д. Методика однофакторного регрессионного анализа включает в себя выполнение следующих процедур. Построение корреляционного поля. Эта процедура сводится к нанесению в плоскости XY точек результатов эксперимента. Проведение визуального анализа полученного поля. По тесноте и характеру расположения точек можно ориентировочно судить о виде регрессионной зависимости между параметром y и его фактором x. В случае большого объема экспериментальных данных вместо корреляционного поля строится эмпирическая линия регрессии. Для этого диапазон изменения фактора x разбивается на произвольное число равных интервалов. Для каждого интервала определяется среднее значение исследуемого параметра y  , i = 1, 2, …, n,где  - среднее арифметическое значение параметра y в i – й группе;yij – j‑е значение параметра y вi – й группе; n – число групп, m – число значений параметра y в i – й группе. Далее на плоскости XY наносят точки средних значений  ,  (i = 1, 2,…, n) и соединяют их отрезками прямых линий. Полученная ломаная линия является эмпирической линией регрессии. Ее вид позволяет принять решение о виде теоретической регрессионной зависимости между параметром y и его фактором x.Аппроксимация в соответствии с видом эмпирической линии регрессии ее теоретической регрессионной зависимостью, например линейной  ;параболой второго порядка  ;параболой третьего порядка  ;гиперболой  и др.Определение неизвестных коэффициентов ai выбранной регрессионной зависимости. Обычно определение коэффициентов регрессионной зависимости осуществляют методом наименьших квадратов, согласно которому сумма квадратов отклонений теоретических значений исследуемого параметра от экспериментальных должна быть минимальной. Проверка адекватности теоретической регрессионной зависимости. Она в зависимости от условий (малый или большой объем выборки и др.) может осуществляться с использованием критериев Фишера (для малых выборок), Пирсона, Романовского и др. Сущность проверки на адекватность заключается в сопоставлении результатов расчета по полученной теоретической модели (регрессионной зависимости) исследуемого параметра объекта с экспериментальными данными. Для этого рассчитывается экспериментальное (опытное) значение критерия, например, Фишера kэ и сравнивается с его теоретическим (табличным) kт, выбираемым при требуемой доверительной вероятности p ( обычно p = 0,95). Если kэ<kт – модель адекватна, в противном случае – модель неадекватна. Опытное значение критерия Фишера kэ вычисляется по формуле  ,где 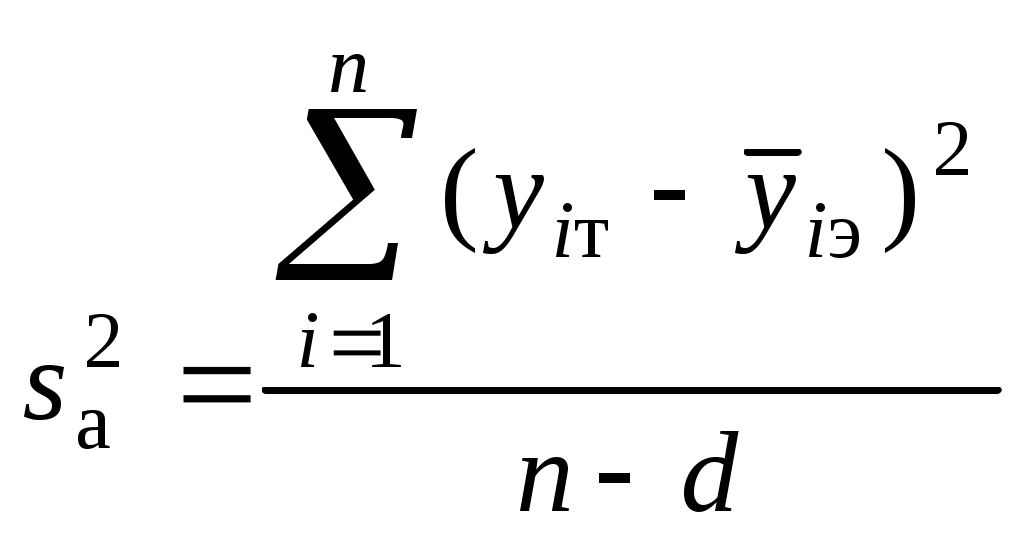 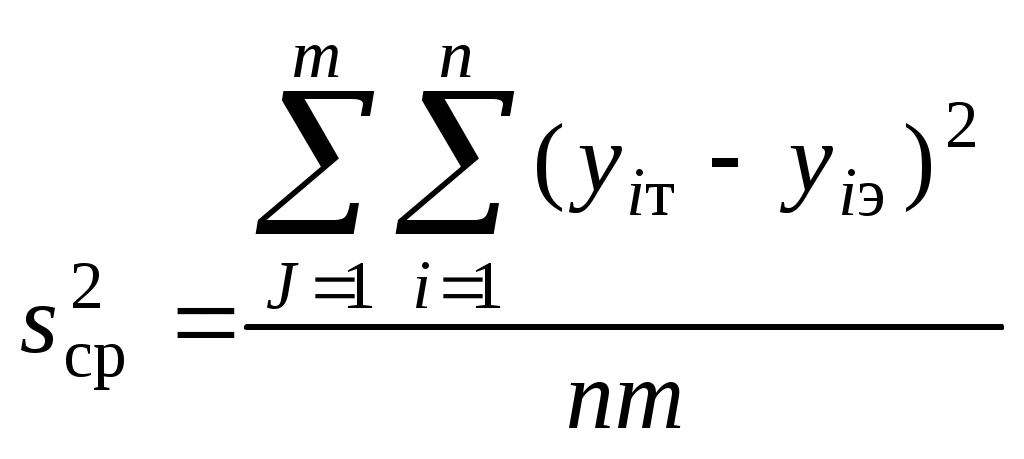– дисперсия адекватности;  – средняя дисперсия всех результатов эксперимента. Эти дисперсии определяются по формулам [3]: ;  ,в которых yiТ, yiэ – теоретические и опытные значения параметра y в i – й группе;  , - опытное среднее арифметическое значение параметра y в i – й группе;d – число коэффициентов теоретического уравнения регрессии. Значение kт принимается из таблицы, приводимой во многих литературных источниках по математической статистике. Входными данными для выбора теоретического значения критерия Фишера являются уровень доверительной вероятности p и числа f1, f2 степеней свободы, определяемые как f1 = n-d и f2= n(m-1). Задание В таблицах 3-12 приведены результаты экспериментальных исследований взаимосвязей параметров и факторов процесса механической обработки деталей. Задачей исследований являлась проверка достоверности рабочей гипотезы о наличии связи между исследуемым параметром и фактором режима обработки, ее силе и вида уравнения регрессии этой связи. Выполнить корреляционный и регрессионный анализы опытных данных и сформулировать основные выводы о наличии связи исследуемого параметра качества обработанной детали (процесса обработки) с варьируемым фактором, ее силе и виде эмпирической зависимости, отражающей эту связь1. Варианты заданий приведены в таблица 2. Таблица 2. Варианты заданий
|
