Документ Microsoft Office Word. 19. Описать способы проверки независимости дискретных случайных величин и получения рядов распределений их суммы и произведения
 Скачать 0.94 Mb. Скачать 0.94 Mb.
|
|
19. Описать способы проверки независимости дискретных случайных величин и получения рядов распределений их суммы и произведения.  Произведением случайных величин Х иYназывается случайная величина XY, возможные значения которой равны произведениям каждого возможного значения Х на каждое возможное значение Y;а вероятности возможных значений произведения XY равны произведениям вероятностей одного сомножителя на условную вероятность другого: Если величины Х иYнезависимы, то равенство (10.4.1) примет вид: Суммой двух дискретных случайных величин Х и Y называется случайная величина X+Y, возможные значения которой равны суммам каждого возможного значения Х с каждым возможным значением Y; а вероятности возможных значений суммы X+Y равны произведениям вероятностей возможных значений слагаемых, для зависимых величин - произведениям вероятности одного слагаемого на условную вероятность другого, т.е. Если величины Х и Y независимы, то условные вероятности становятся безусловными. В этом случае равенство (11.4.4) примет вид: Таким образом, вероятности суммы задаются так же, как вероятности произведения случайных величин. Например, если вероятность возможного значения х1 равна р1, а вероятность возможного значения у1 равна g1, то вероятность возможного значения х1+у1 равна 25. Охарактеризовать случайные величины, имеющие нормальный закон распределения. Описать их функции распределения и плотности распределения. Объяснить роль функции Лапласа для характеристики нормального распределения и перечислить ее свойства. Нормальный закон распределения наиболее часто встречается на практике. Главная особенность, выделяющая его среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях. СВ X распределена по нормальному закону, если ее функция плотности распределения вероятностей имеет вид: 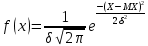 , где , где MX – математическое ожидание СВ X (MX=a) 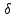 – среднеквадратическое отклонение – среднеквадратическое отклонение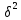 – дисперсия СВ X (DX= – дисперсия СВ X (DX=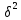 ) )Функция распределения случайной величины Х, распределенной по нормальному закону, выражается через функцию Лапласа Ф(х) по формуле: 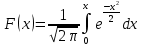 Свойства функции Лапласа: 1) область определения функции Лапласа – вся числовая ось - (-∞, +∞) 2) функция Лапласа монотонно возрастает на всей числовой прямой 3) Функция f{x) может принимать только положительные значения, т. е. f(x}>0 4) Функция Лапласа нечетна, т.е. 4) График функции f(x) симметричен относительно прямой х = а. 5) F(x – a) = f(a – x), то есть график симметричен относительно прямой х = а. 6) 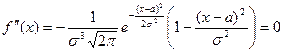 при при 31. Дать определения основных выборочных числовых характеристик: средней, дисперсии, среднего квадратического отклонения. Перечислить их свойства. Пусть выборка объема nпредставима в виде вариационного ряда. Если все значения признака выборки различны, то выборочная средняя определяется по формуле: 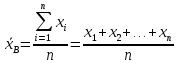 Если значения признака имеют соответствующие частоты, то выборочная средняя равна 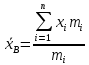 Т.е. выборочная средняя рассчитывается по формуле средней арифметической взвешенной. Выборочную среднюю можно рассматривать как СВ, а, следовательно, можно говорить о распределениях выборочной средней и о числовых характеристиках этого распределения. Выборочная средняя является оценкой МО СВ и представляет собой несмещенную оценку, т.к. 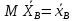 . .Выборочная средняя является и состоятельной оценкой генеральной средней, т.к. при увеличении объема выборки n, выборочная средняя стремится по вероятности к генеральной средней. Таким образом, если по нескольким выборкам достаточно большого объема из одной той же генеральной совокупности будут найдены выборочные средние, то они будут приближенно равны между собой. В этом состоит свойство устойчивости выборочных средних. Выборочная средняя является эффективной оценкой генеральной средней. Средняя выборочная обладает рядом свойств, аналогичных свойствам математического ожидания, а именно 1. Средняя выборочная постоянной равно самой этой постоянной. 2. Если все варианты умножить или разделить на одно и тоже число к, то будет выполнено равенство 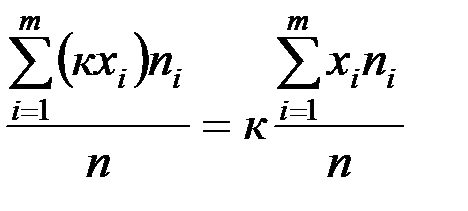 , т.е. постоянную величину можно выносить за знак выборочной средней. Иначе говоря, если все варианты увеличить или уменьшить в одно и тоже число раз, то и средняя выборочная также увеличиться или уменьшится в это же число раз. , т.е. постоянную величину можно выносить за знак выборочной средней. Иначе говоря, если все варианты увеличить или уменьшить в одно и тоже число раз, то и средняя выборочная также увеличиться или уменьшится в это же число раз.3. Если все варианты увеличить или уменьшить на одно и тоже число раз с, то и средняя выборочная увеличиться или уменьшится на это же число раз, т.е. 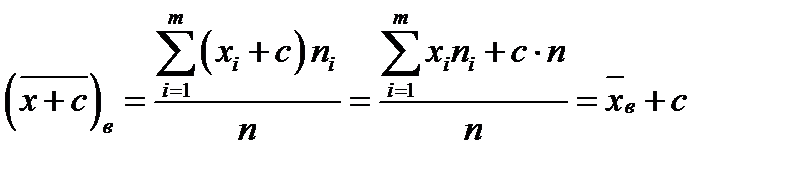 . .4. Средняя выборочная алгебраической суммы двух (или нескольких) признаков равна алгебраической сумме средних выборочных этих признаков, т.е. 5. Если выборочные данные разделены на некоторые группы, то общая средняя всех данных вычисляется по формуле 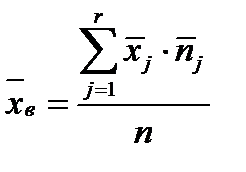 , ,где r – число групп; 6. Если все частоты вариантов умножить на одно и тоже число, то средняя выборочная не изменится. 7. Средняя выборочная отклонений вариантов от средней выборочной равна нулю, т.е. 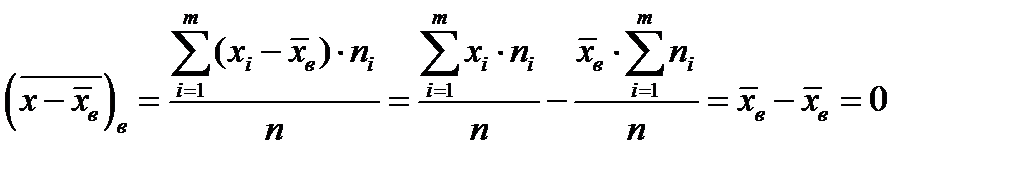 Для характеристики рассеяния наблюдаемых значений около выборочной средней вводится выборочная дисперсия, вычисленная по формуле: 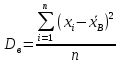 , , 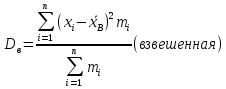 . .Для вычисления дисперсии выборочной можно воспользоваться формулой: 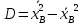 Выборочная дисперсия является точечной оценкой генеральной дисперсии. Она является эффективной, состоятельной и смещённой. Для устранения смещенности вводится исправленная выборочная дисперсия 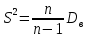 Свойства выборочной дисперсии: Величина дисперсии не изменится, если увеличить или уменьшить значения вариант на одно и то же число. Для определенности увеличим все варианты на число С и рассмотрим условную выборку с членами х;. + С. Согласно теореме 1.1 средняя выборочная новой выборки увеличится на то же число и составит хв + С.По формуле (1.11) найдем дисперсию новой выборки: 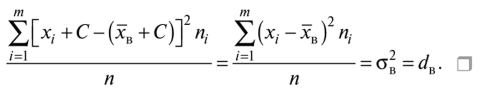 Если все значения выборки увеличить (уменьшить) в к раз, то дисперсия увеличится (уменьшится) в к2 раз, а среднее квадратическое отклонение — в к раз. Составим новую выборку с условными членами {кх^. Согласно теореме 1.2 ее средняя выборочная увеличится тоже в к раз и составит к хв. Дисперсию новой выборки найдем по формуле : 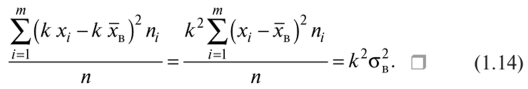 Если частоты вариант увеличить или уменьшить в одно и то же число раз, то дисперсия не изменится. Для определенности рассмотрим новую выборку, в которой частоты членов увеличены в / раз. Тогда дисперсия новой выборки составит 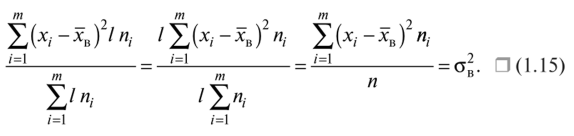 Дисперсия признака, некоторой совокупности (генеральной или выборочной) равна разности средней арифметической ее квадрата и квадрата ее среднего значения, т.е. Проверим справедливость этой формулы для выборочной дисперсии. С этой целью возьмем соотношение (1.11) и проведем в нем несложные преобразования. В результате получим 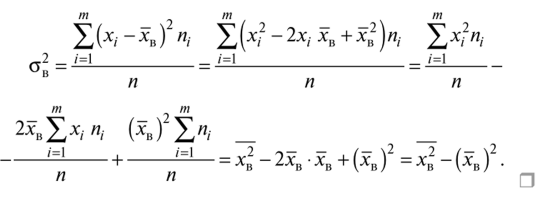 Выборочное среднее квадратическоеотклонение выборки определяется формулой: Особенность выборочного среднего квадратического отклонения состоит в том, что оно измеряется в тех же единицах, что и изучаемый признак. 32. Объяснить сущность метода произведения для вычисления выборочных средней и дисперсии. Cм. 31 35. Привести доверительные интервалы для оценок средней и дисперсии генеральной совокупности по малой выборке. Указать теоретические основания для этих оценок. Пусть СВ Х распределена по нормальному закону, для которого известна 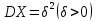 . Из генеральной совокупности делается выборка объема n. Выборка х1, х2,…, хn рассматривается как n независимых СВ, распределенных также, как Х. Это значит, что MX1=MX2=…=MXn=MX, DX1=DX2=…=DXn=DXи . Из генеральной совокупности делается выборка объема n. Выборка х1, х2,…, хn рассматривается как n независимых СВ, распределенных также, как Х. Это значит, что MX1=MX2=…=MXn=MX, DX1=DX2=…=DXn=DXи 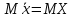 , , 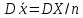 Обозначим неизвестную величину MX=aи поберем по заданной надежности 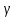 положительной число d>0' так, чтобы выполнялось условие положительной число d>0' так, чтобы выполнялось условие 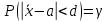 Так как 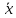 является СВ, которая распределена по нормальному закону с МО и является СВ, которая распределена по нормальному закону с МО и 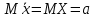 и и 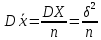 Тогда 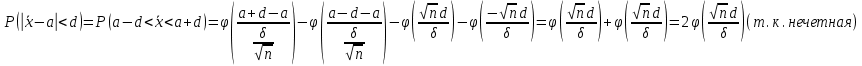 Нужно подобрать число d таким образом, чтобы 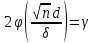 или или 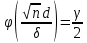 Для любого 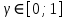 можно по таблице найти такое числоt, для которого будет выполняться можно по таблице найти такое числоt, для которого будет выполняться 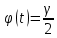 . Число tназывается квантилем. Тогда из равенства . Число tназывается квантилем. Тогда из равенства 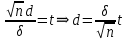 . Тогда . Тогда 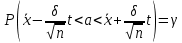 Таким образом, с надежностью 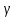 доверительный интервал доверительный интервал 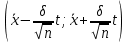 покрывает неизвестный параметр MX=a. Или точечная оценка покрывает неизвестный параметр MX=a. Или точечная оценка 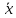 определяет значение параметра MX с точностью определяет значение параметра MX с точностью 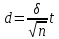 и надежностью и надежностью 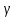 . . |
