Электротехника. Методические указания и контрольные задания для студентов заочного отделения по специальности 151001 Технология машиностроения
 Скачать 1.15 Mb. Скачать 1.15 Mb.
|
1 2 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Сибирский государственный аэрокосмический университет имени академика М.Ф.Решетнева» (СибГАУ) Аэрокосмический колледж
(Наименование учебной дисциплины) Методические указания и контрольные задания для студентов заочного отделения по специальности 151001 «Технология машиностроения»
Красноярск, 2012 г. Указания к решению контрольных задач Задача № 1 (типовой пример) Решение этой задачи требует знания закона Ома для всей цепи и ее участков, первого закона Кирхгофа и методики определения эквивалентного сопротивления цепи при смешенном соединении резисторов. Дано: Для цепи постоянного тока, изображенной на рисунке, определить токи и напряжения на всех участках цепи 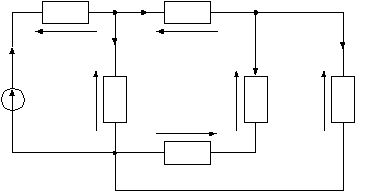 R1 a I3 R3 c R1 a I3 R3 cI2 I6 U1 U3 I4 I1 + E U2 R2 U4 R4 U6 R6 – U5 b R5 Рис. 1.1 –Исходная схема цепи Найти:
а) баланс токов, б) баланс мощности.
Решение:
Свертываем цепь (прямой путь). Первое преобразование (Рис. 1.2). R1 a I3 R3 c 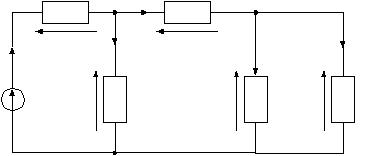 I2 I6 U1 U3 I4 I1 + E U2 R2 U7 R7 U6 R6 – b Рис. 1.2 – Расчетная схема после первого преобразования Так как цепь имеет один источник питания, то токи на схеме можно расставить сразу правильно. Расставляем стрелки напряжений на всех участках цепи против стрелок токов. Проводим второе преобразование цепи (Рис.1.3): R1 a I3 R3 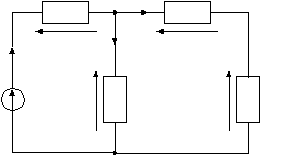 I2 U1 U3 I1 + E U2 R2 U8 R8 – b Рис. 1.3– Расчетная схема после второго преобразования Третье преобразование (Рис.1.4): R1 a I3 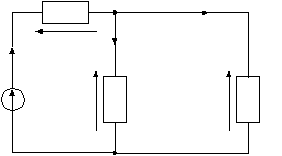 I2 U1 I1 + E U2 R2 U9 R9 – b Рис. 1.4 – Расчетная схема после третьего преобразования Четвертое преобразование (Рис.1.5): R1 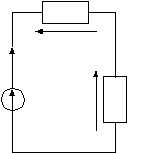 U1 I1 + E U10 R10 – Рис. 1.5 – Расчетная схема после четвертого преобразования Последнее, пятое преобразование (Рис.1.6): I1 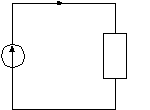 + E RЭКВ – Рис. 1.6 – Расчетная схема после пятого преобразования Определяем ток I1 в схеме на рис. 1.6 по закону Ома.
Эти токи можно найти по-другому, например, из рисунка 1.3: Переходя к рисунку 1.2, определяем токи I4 и I6. Согласно второму закона Кирхгофа имеем Uаб + U1 = E , откуда Uаб = E – U1 , напряжение U1 определяется по закону Ома, U1 = R1I1 = 2 5 = 10 B, тогда напряжение Uаб будет равно: Uаб = 30 – 10 = 20 В. Окончательно искомые токи будут равны:
а) баланс токов: из рисунка 1.2 следует: Сходимость баланса токов: б) баланс мощности. Мощность вырабатываемая генератором: Мощность нагрузки: Сходимость баланса мощности определяется так:
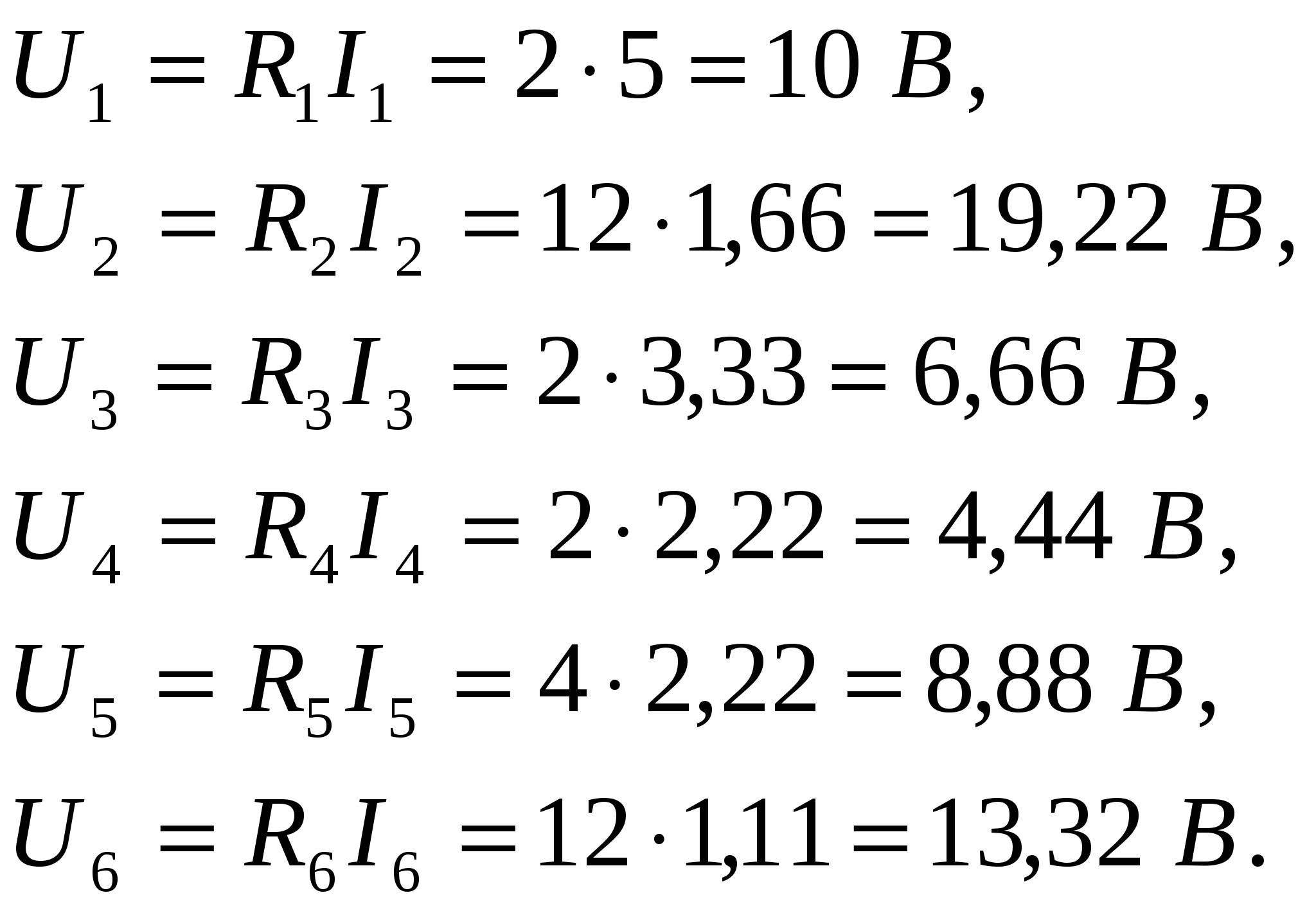
Первое уравнение: Сходимость баланса Второе уравнение: Сходимость баланса Третье уравнение: Сходимость баланса Если балансы тока, напряжения и мощности сошлись с погрешностью не более 1%, то расчет считается выполненным правильно. Задача № 2 (типовой пример) Решение этой задачи требует знания первого и второго законов Кирхгофа и методики расчета сложной цепи различными методами. Дано: Для сложной электрической цепи, изображенной на рис 2.1, определить токи в ветвях методом контурных токов. R1 R4 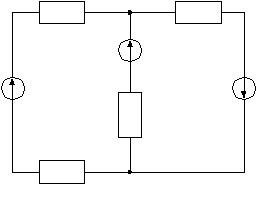 + E2 + – + E1 E3 – R2 – R3 Рисунок 2.1 – Исходная схема цепи Найти:
Решение:
Определяем число независимых контуров (Ч.Н.К.) в цепи, q – число ветвей в цепи, n – число узлов. R1 R4 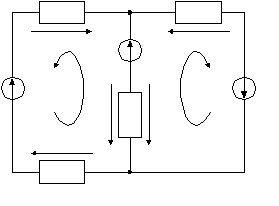 U11 + U42 E2 _ + + E1 J1 J2 E3 _ _ U21 U22 R2 U31 R3 Рисунок 2.2 – Расчетная схема к методу контурных токов
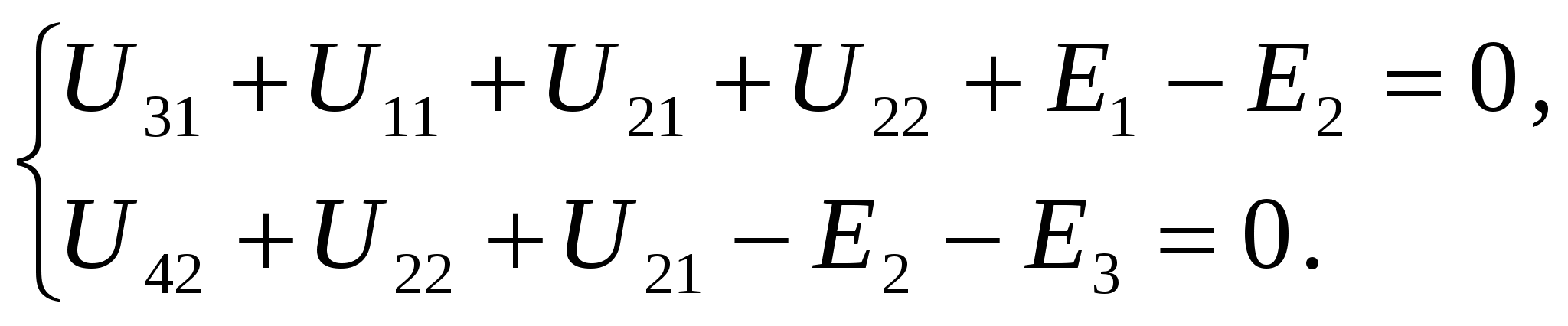 Раскрываем напряжения через закон Ома и получаем 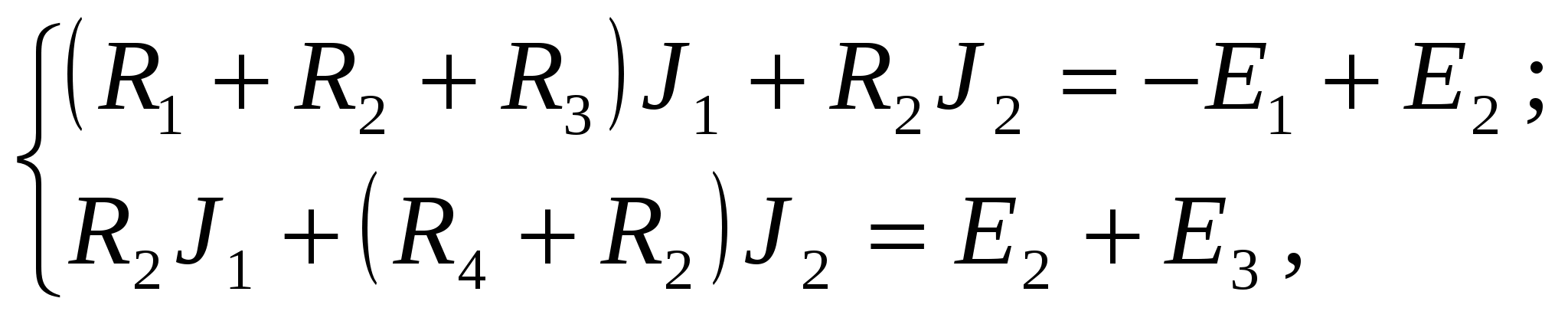 где 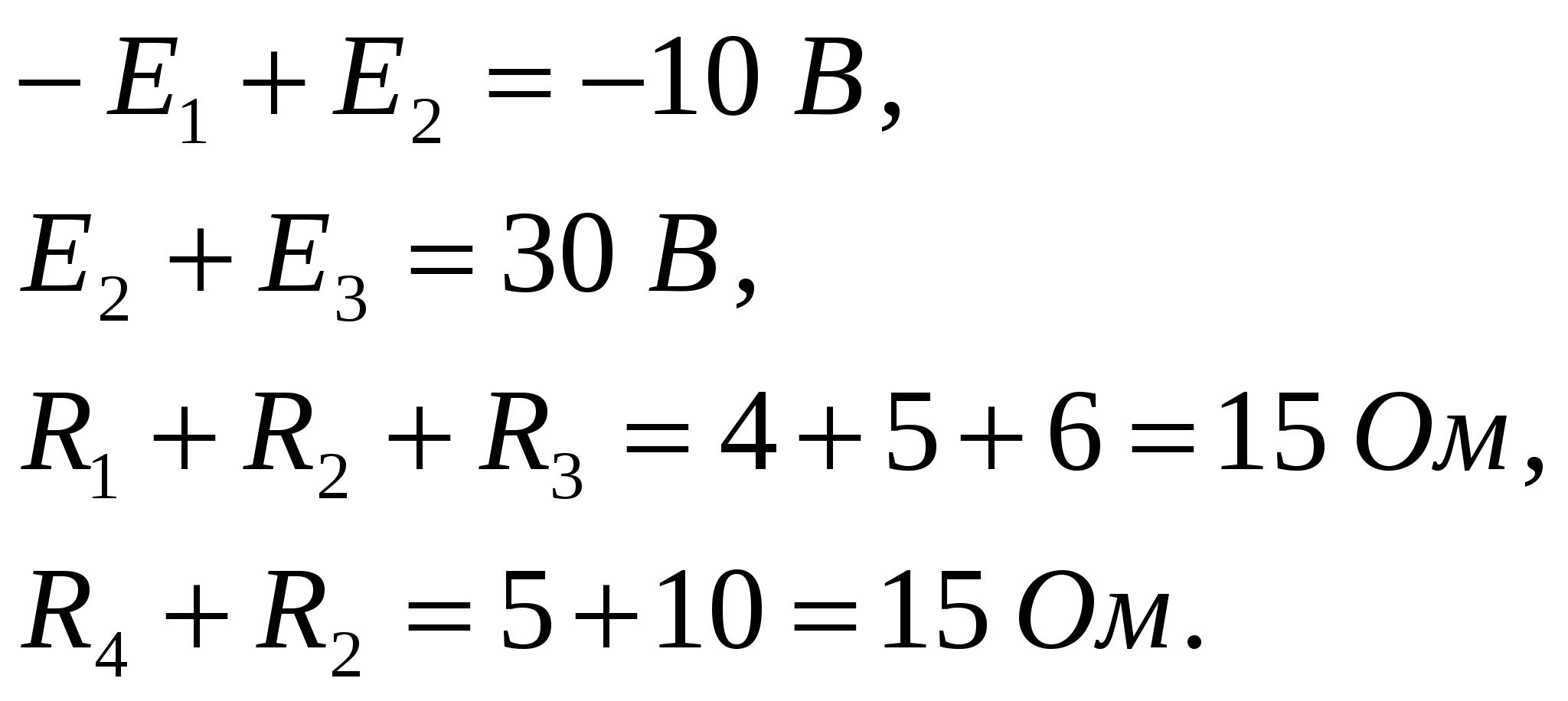 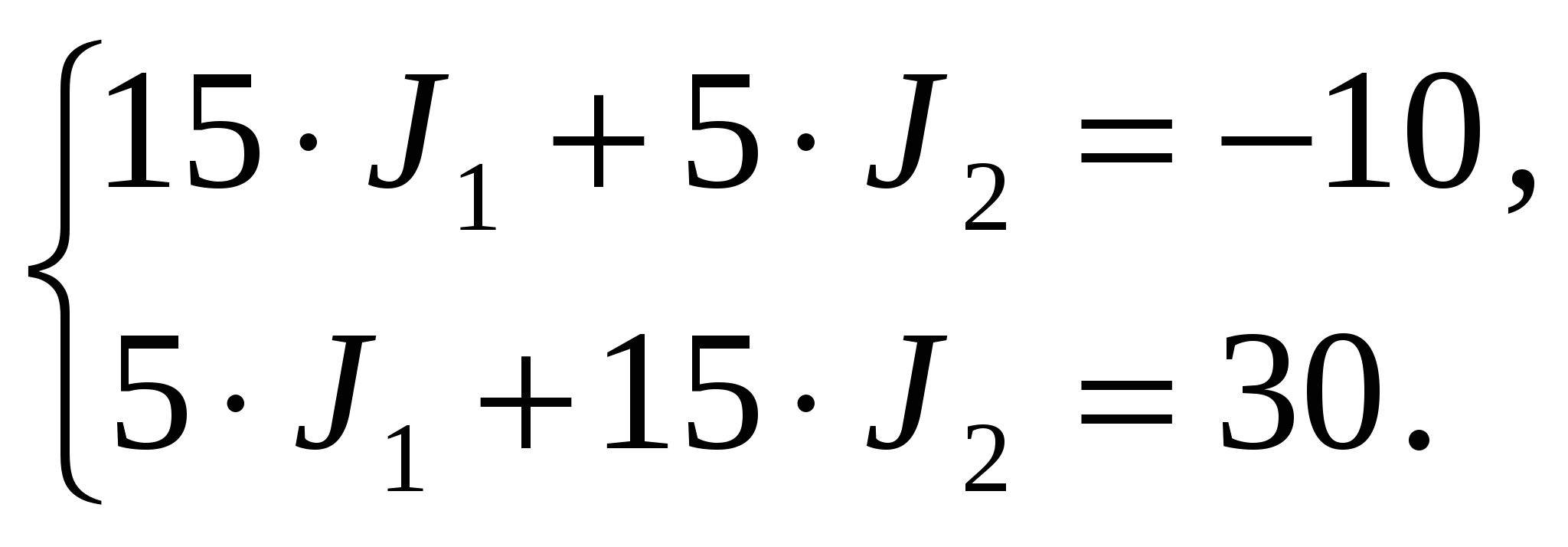
Расчет токов производится с точностью до 2-х знаков после запятой.
R1 R4 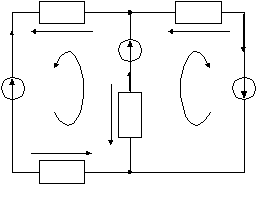 A AI1 U1 + U4 I3 E2 _ + + E1 J1 I2 J2 E3 _ _ U2 R2 U3 R3 B Рисунок 2.3– Определение реальных токов цепи Из схемы, сопоставляя реальные и контурные токи, запишем 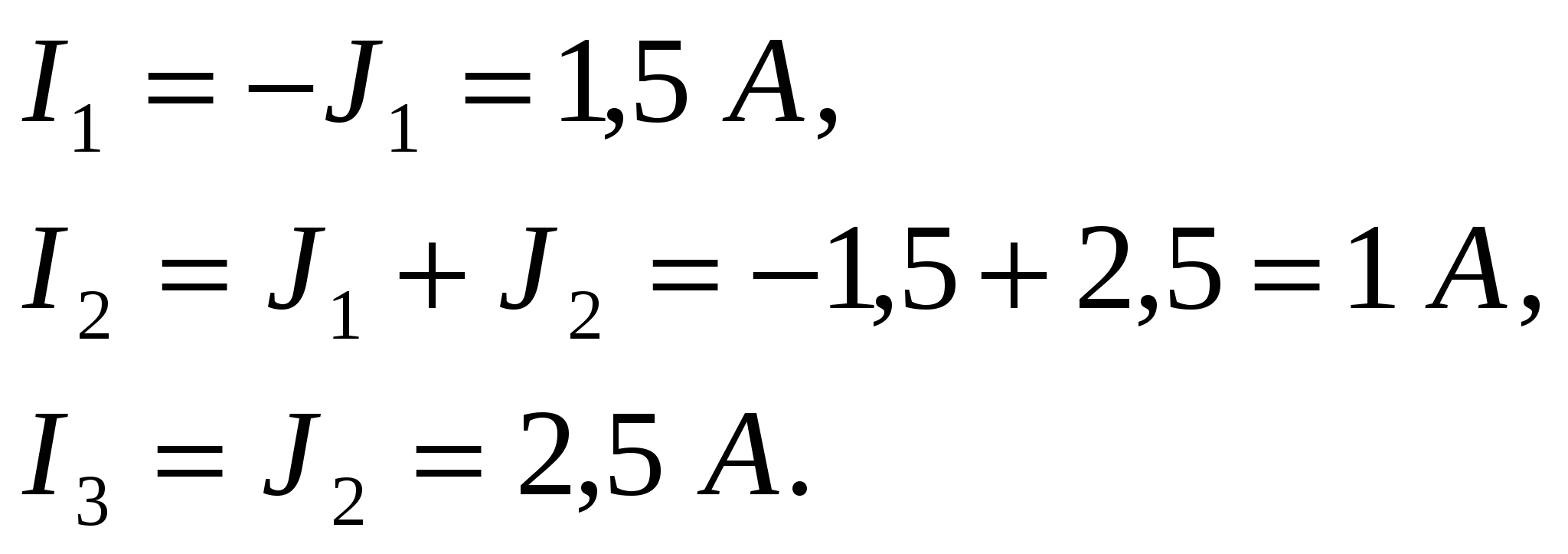 Если реальный ток получается с отрицательным знаком, то это означает, что ток течет в направлении, противоположном направлению стрелки на чертеже. При этом никаких изменений на схеме делать не нужно, а в дальнейших расчетах следует использовать значение полученного тока с его знаком.
Проверку производим по первому закону Кирхгофа во всех независимых узлах.
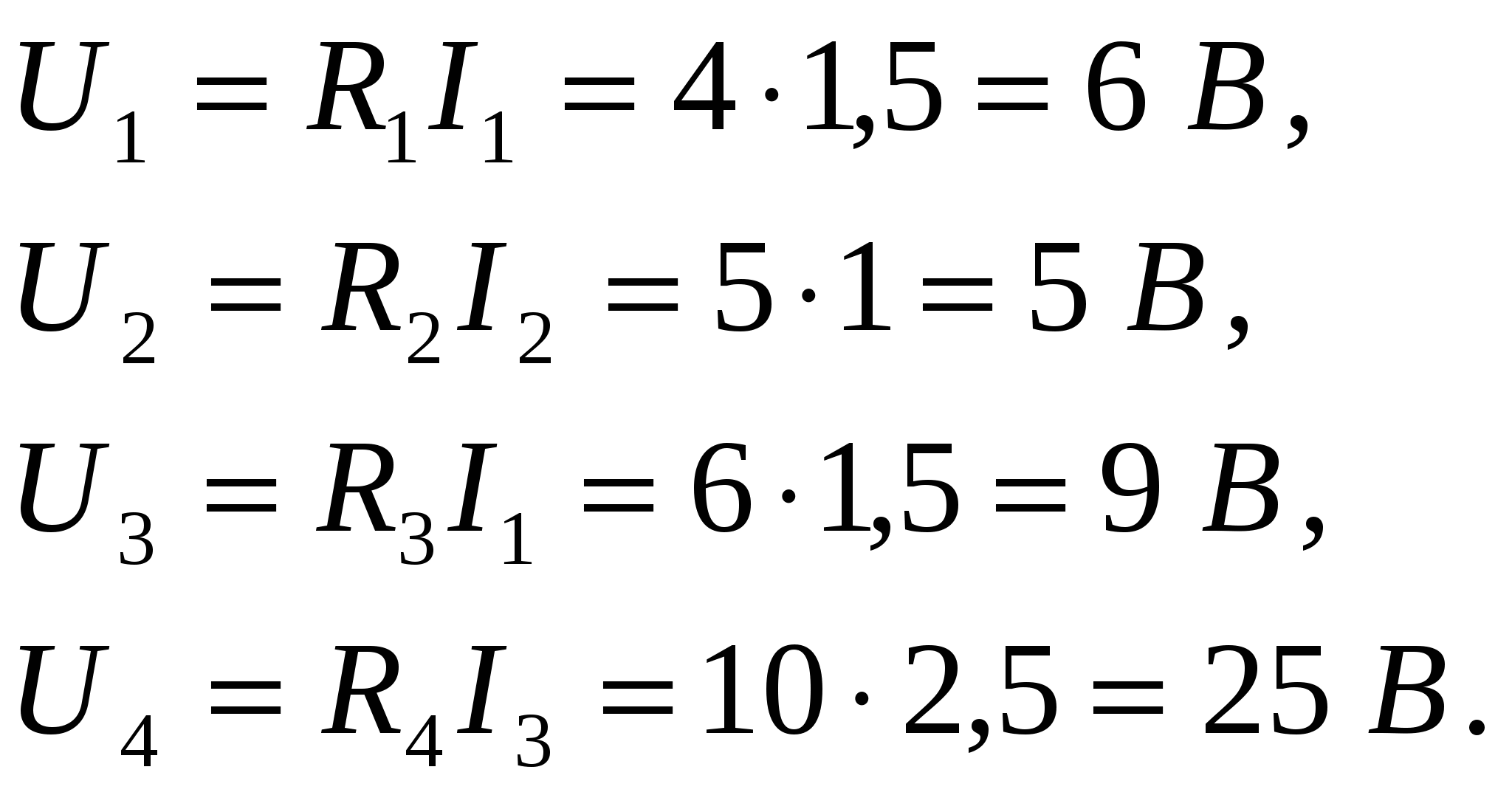 10.Проверяем напряжения на баланс напряжений. Проверку производим по всем независимым контурам по рисунку 2.3 по второму закону Кирхгофа. 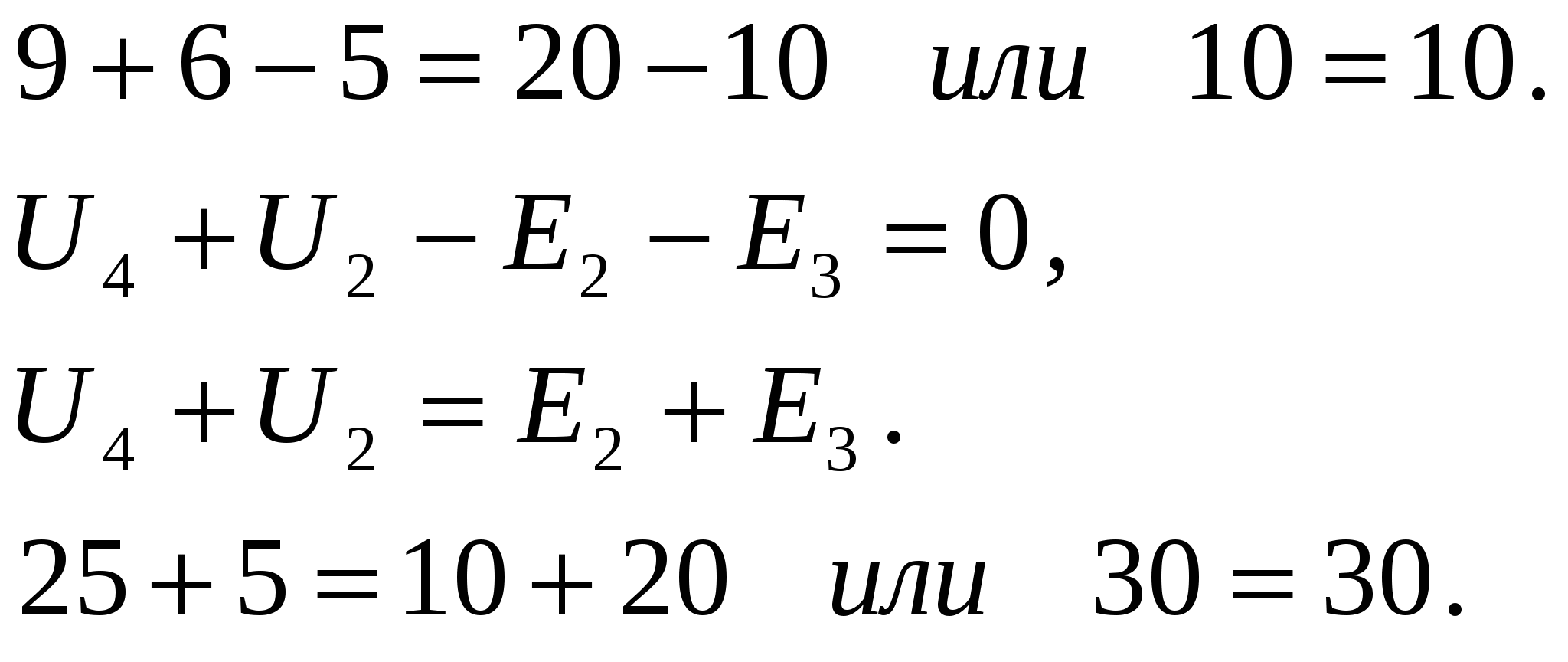
Выражение записывается согласно расположению стрелок на расчетной схеме (рис. 2.3). Если направление стрелок тока и ЭДС на схеме совпадают, то в балансе мощности произведение В составленное таким образом выражение мощности генераторов подставляют токи с теми знаками, которые были получены в результате расчета. Должно быть: Задача № 3 (типовой пример) Задача относится к теме «Неразветвленные цепи переменного тока». Для ее решения Определить ток в цепи (рисунок 3.1) и напряжение на всех ее элементах и построить векторную диаграмму. Дано R = 8 Ом, L = 0,016 Гн, С = 100 мкФ, U = 100 В, 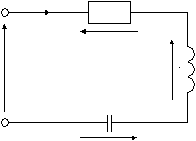 I R I RUR U UL L C UC Рисунок 3.1 – Полная цепь переменного тока Решение:
индуктивное – емкостное – полное сопротивление –
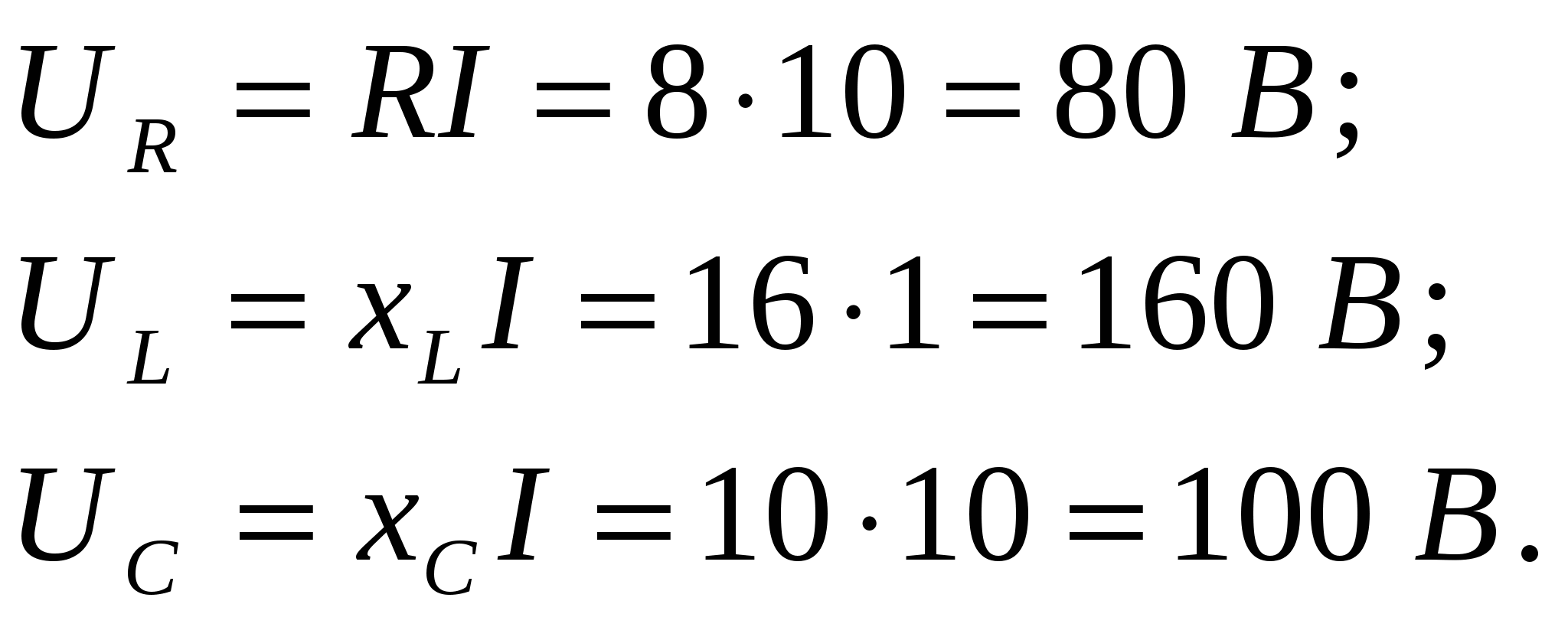 Векторная диаграмма имеет вид, показанный на рисунке 3.2. 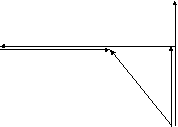 I UL B UX B UX A  A AUC UR UR U U O O Рисунок 3.2– Векторные диаграммы цепи RLC и треугольник напряжений Задача №4 Для решения данной задачи необходимо ознакомится с материалом темы 3.2 Принцип решения задачи рассмотрен в типовом примере 3. Расчет для каждой фазы выполняется отдельно. Задача № 1 (типовой пример) Пример расчета характеристик асинхронного двигателя Ниже рассмотрен расчета основных характеристик асинхронного двигателя. Данный пример приведен как руководство для решения контрольной задачи № 1, контрольной работы № 2 Дано: Для заданного в таблице 1 режима нагрузки производственного механизма построить нагрузочную диаграмму P = f (t), выбрать асинхронный двигатель с короткозамкнутым ротором и определить:
Таблица 1 – Нагрузка на двигатель
Решение:
Для построения диаграммы откладываем мощность Pi по оси координат, а время ti по оси абсцисс. Диаграмма полученная по данным таблицы 2.1 приведена на рисунке 4.1. 30 P, [кВт] 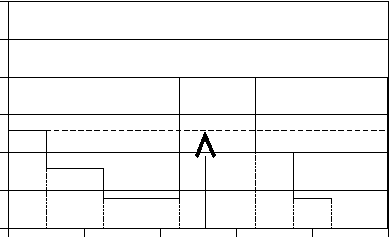 25 20 Р4 15 10 Р1 Р5 Р2 Р3 РЭКВ Р6 5 20 10 10 t, [сек] 0 20 40 60 80 100 Рисунок 4.1 – Диаграмма нагрузки производственного механизма
Находим мощность по формуле 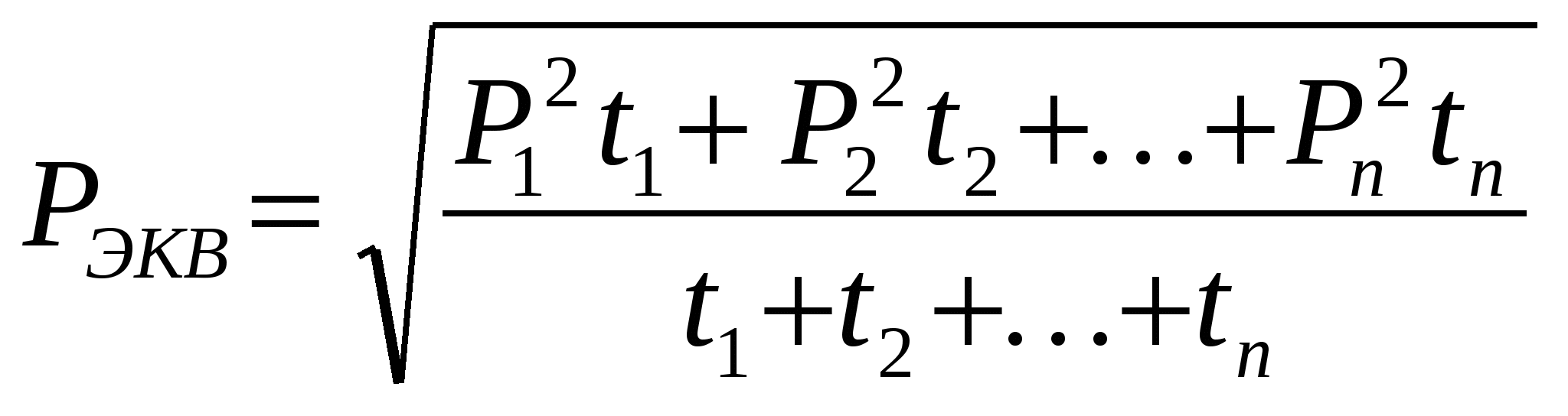 , ,или
Данные выбранного двигателя заносим в таблицу 2.2. Таблица 2. – Технические данные выбранного электродвигателя
Поскольку
Номинальный момент Максимальный момент
Для этого задаем значения скольжения s в пределах от 0 до 1 и по формуле 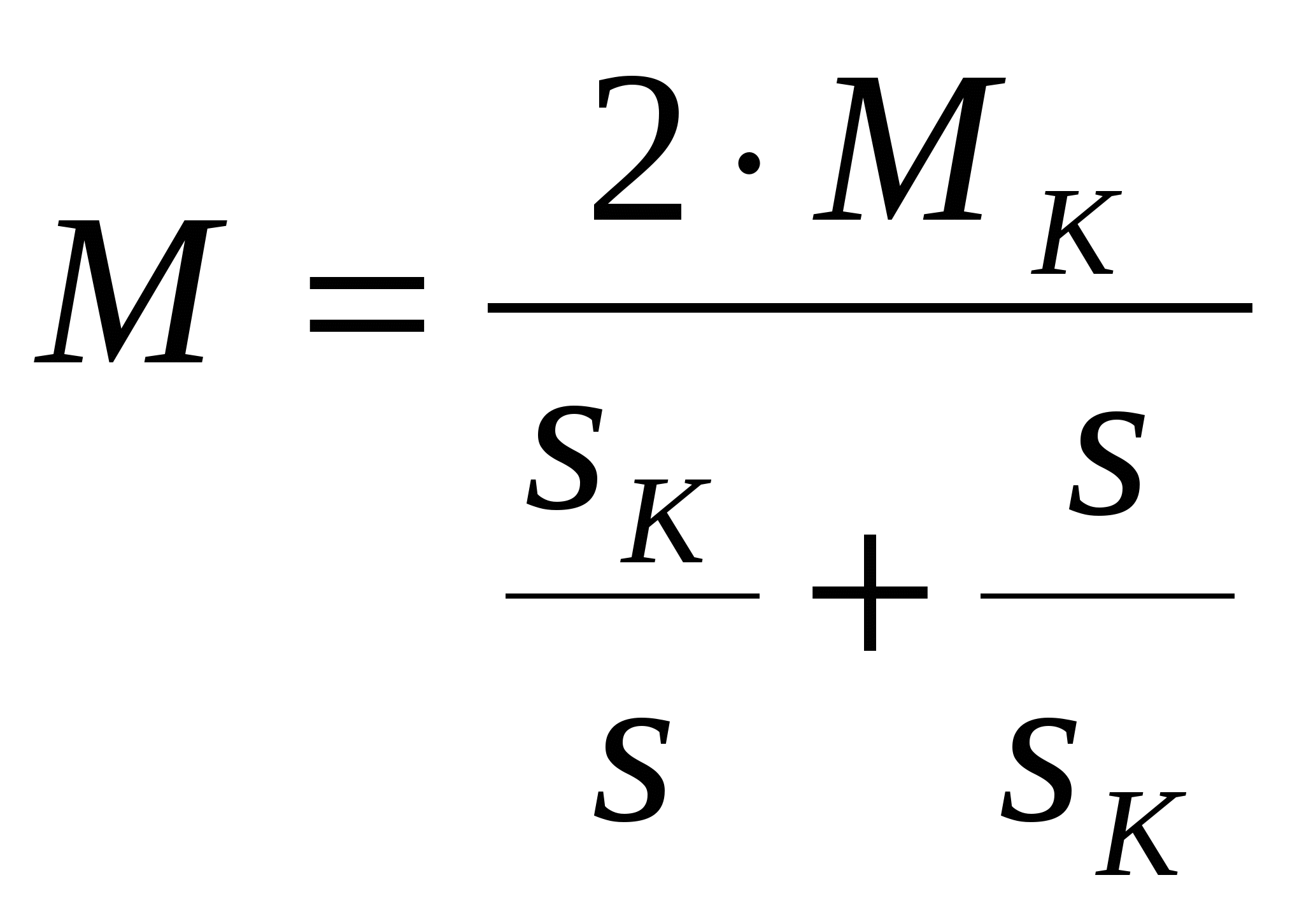 , ,рассчитываем значения вращающего момента.
Для построения этой характеристики пересчитываем значения скольжения в соответствующие им значения частоты вращения вала двигателя по выражению Данные расчетов приведены в таблице 3. Таблица 3 – Данные расчетов для построения скоростной и механической характеристик
По данным таблицы 3 строим характеристики, показанные на рисунке 4.2 и 4.3 соответственно. М, [Нм] 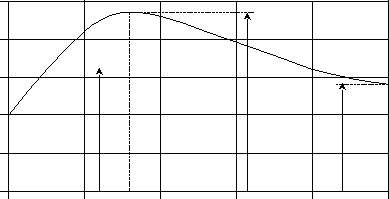 250 250200  150 100 МН МК МПУСК 50 s 0 sH 0,2 sK 0,4 0,6 0,8 1 Рисунок 2.2 – Скоростная характеристика n, [об/мин] 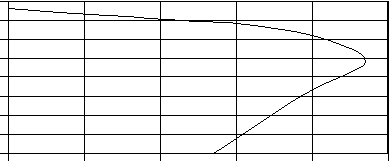 1600 1600 1400 1200 1000 800 600 400 200 М, [Нм] 0 50 100 150 200 250 Рисунок 2.3 – Механическая характеристика Контрольная работа Задача № 1 Для цепи постоянного тока, изображенной на рис. заданы величины сопротивлений и величина ЭДС.
Данные по вариантам приведены в таблице 1 Таблица 1
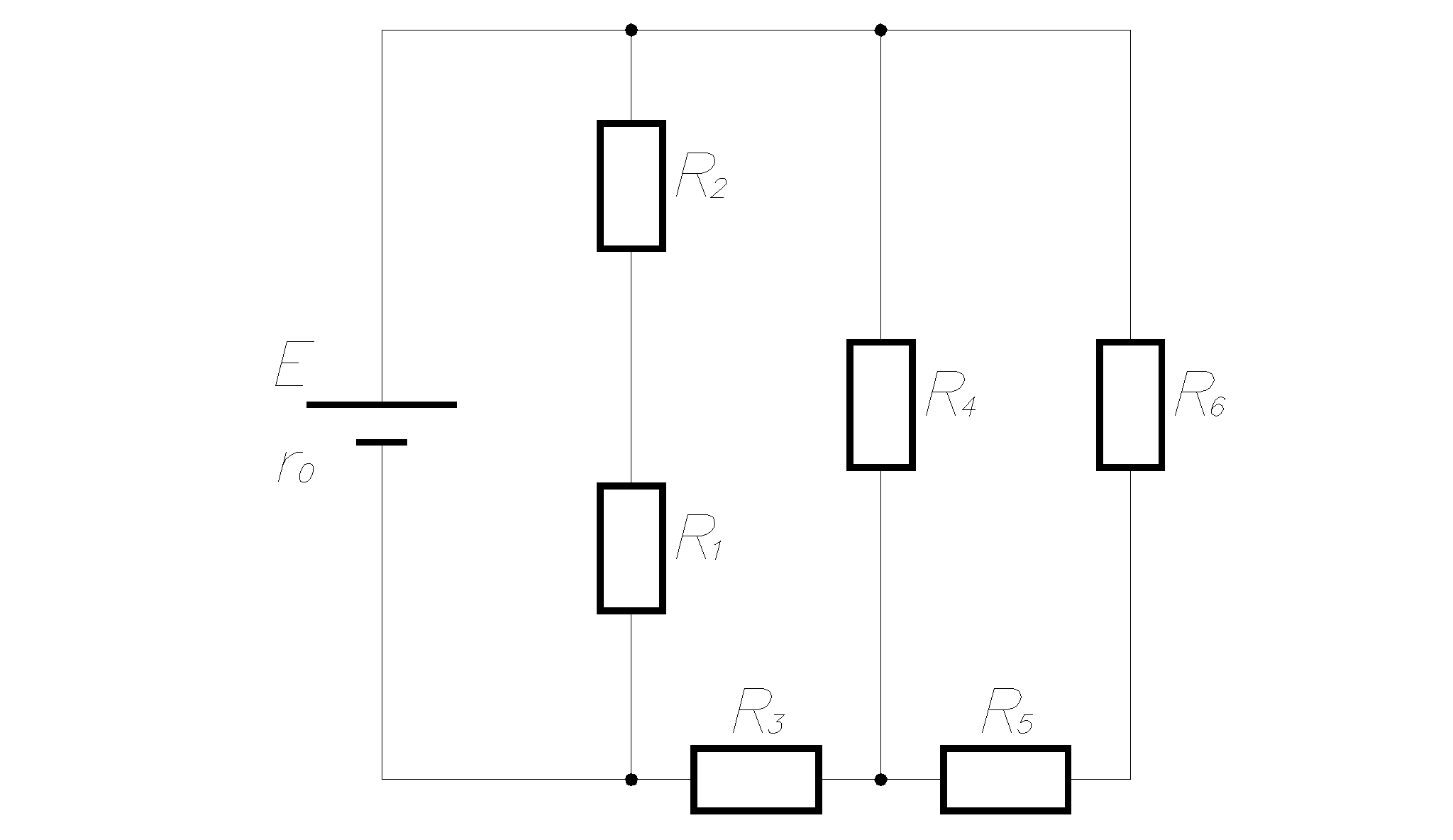 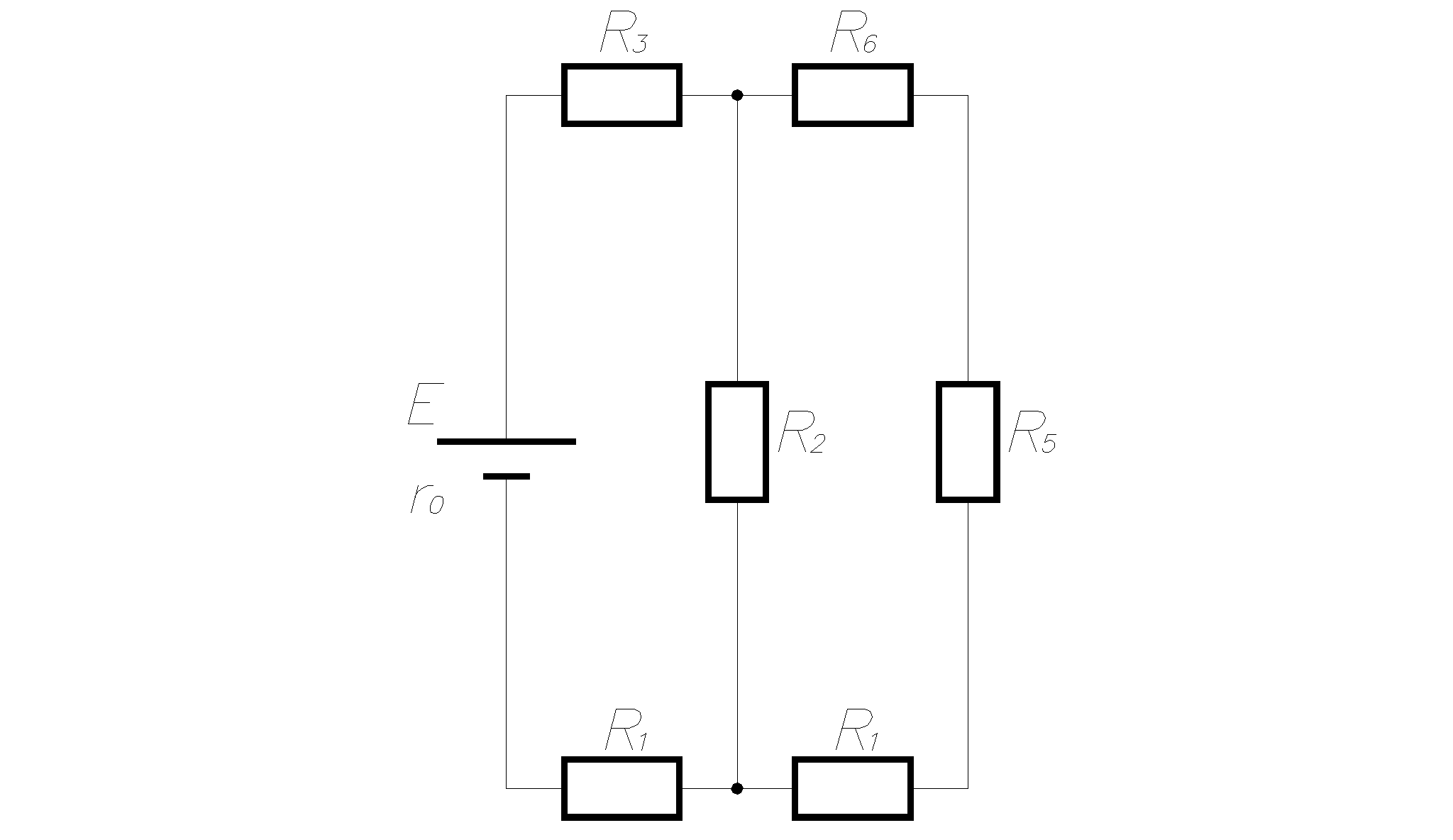 рис1.1 рис1.2 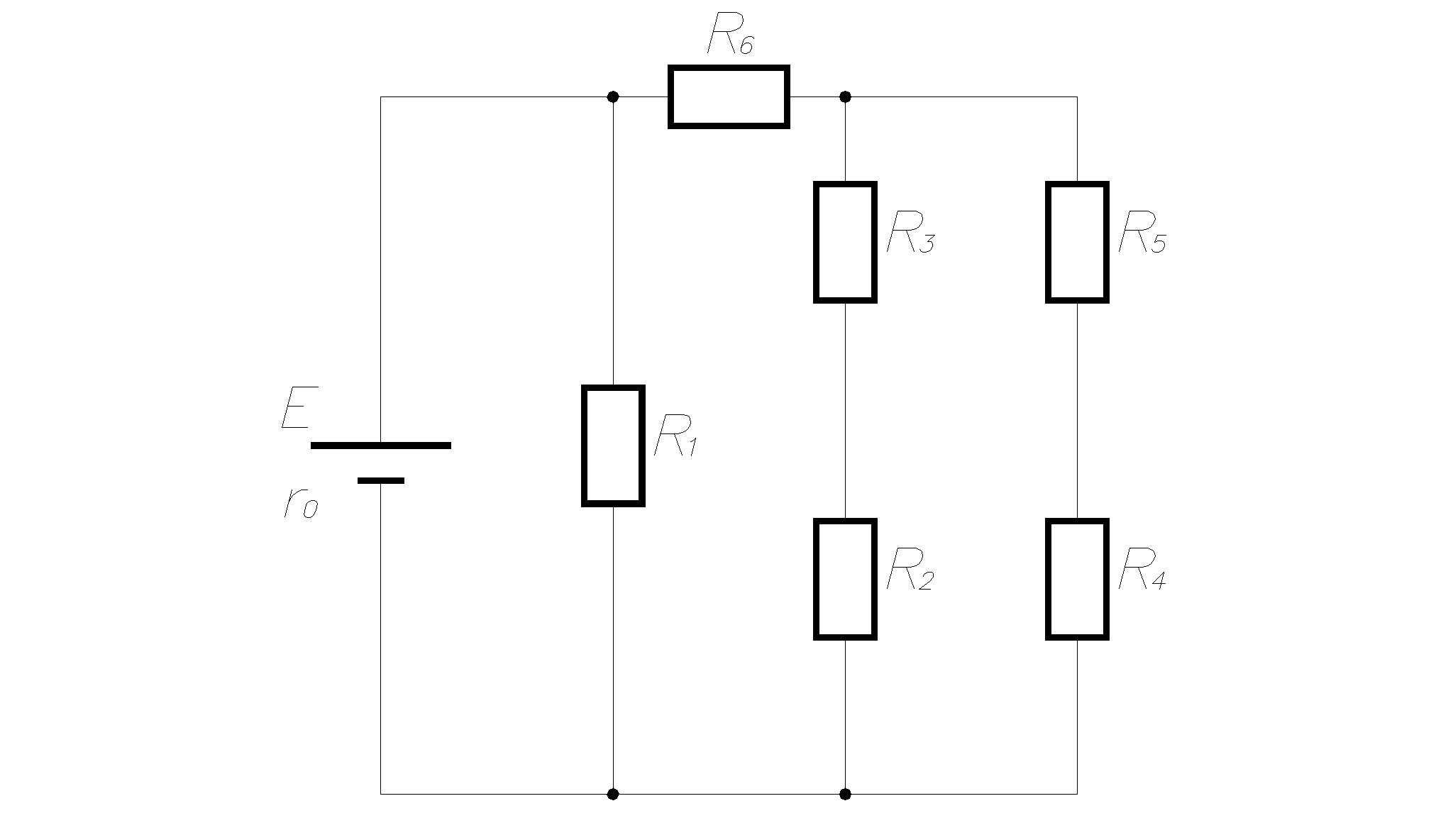 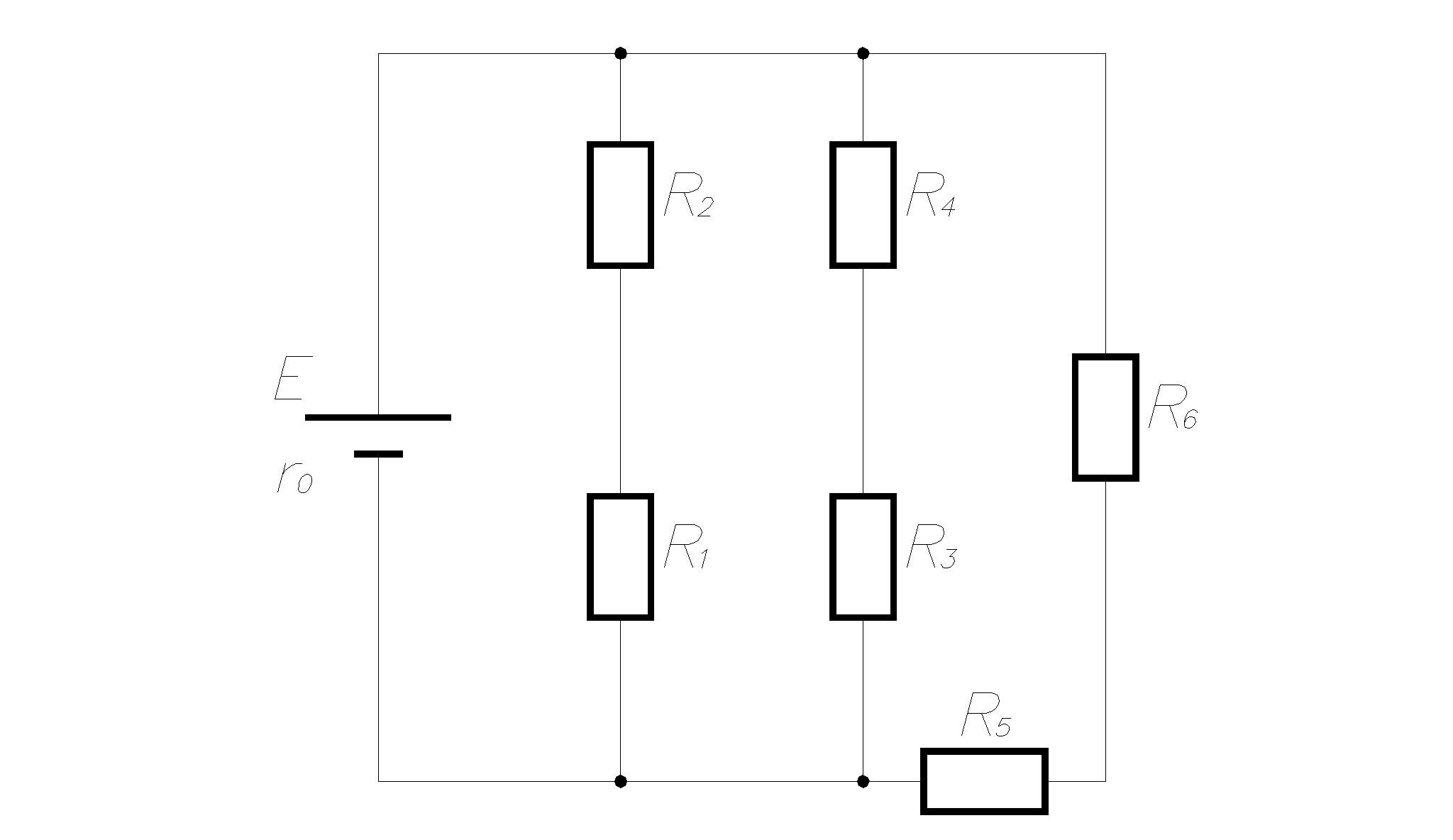 рис1.3 рис 1.4 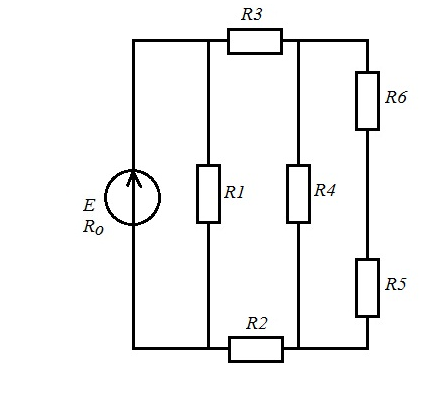 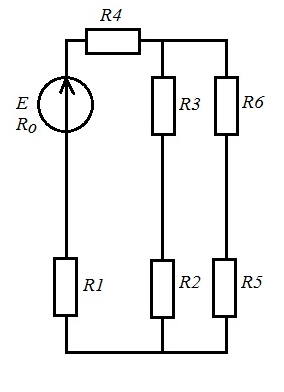 рис 1.5 рис 1.6 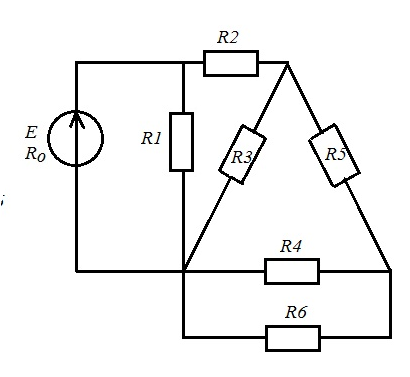 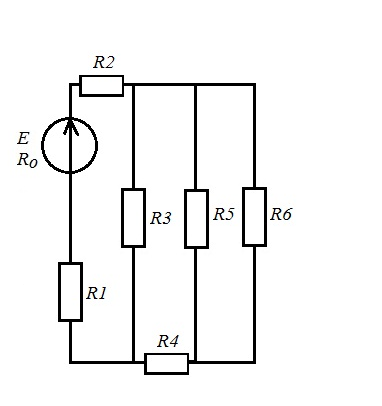 рис 1.7 рис 1.8 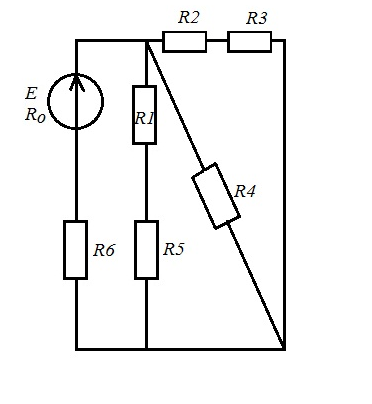 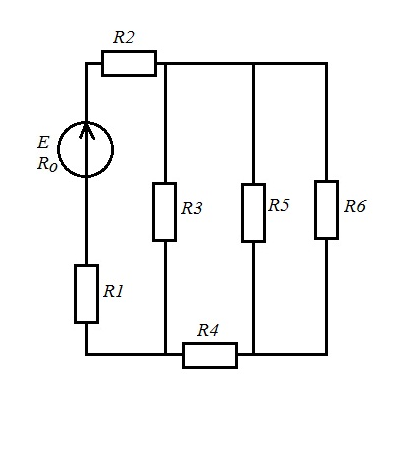 рис 1.9 рис 1.10 Задача № 2 Для сложной электрической цепи, приведенной на рис. выполнить следующее:
Данные по вариантам приведены в таблице 2 Таблица 2
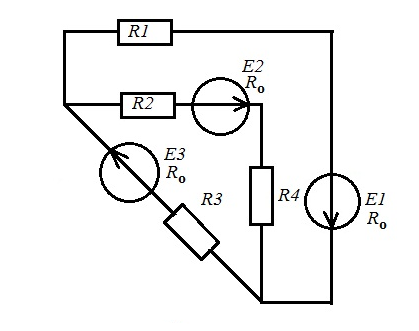 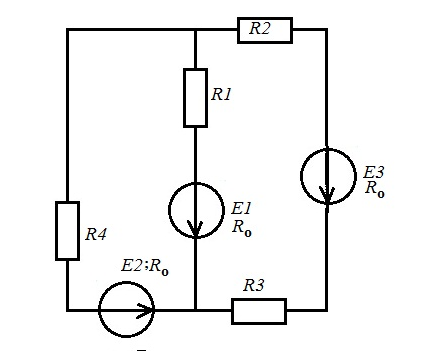  рис 2.1 рис 2.2 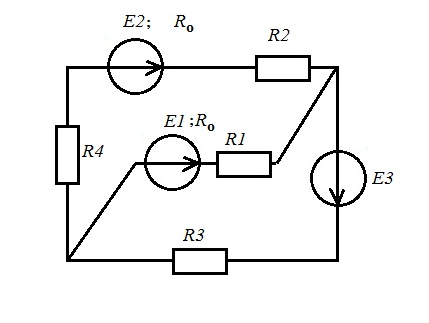 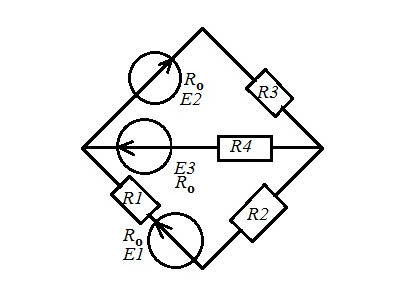 рис 2.3 рис 2.4   рис 2.5 рис2.6   рис 2.7 рис 2.8 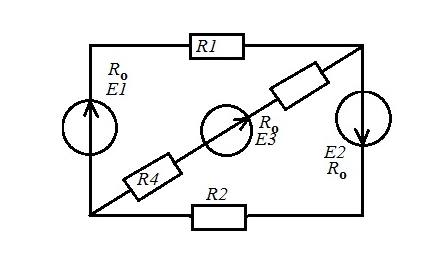 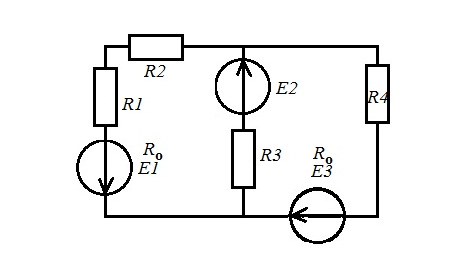 1 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
