Динамическое программирование (методические указания). Методические указания и задания для лабораторной работы по теме Динамическое программирование. Одесса 2004
 Скачать 419.5 Kb. Скачать 419.5 Kb.
|
|
Задача распределения ресурсов. Построение модели ДП и построение вычислительной схемы Задача 1. Планируется распределение начальной суммы средств 0 между п предприятиями П1, П2, ..., Пn. Предполагается, что выделенные предприятию Пk в начале планового периода средства xk приносят доход fk(xk) (k=l,2, ..., n).Будем считать, что: доход, полученный от вложения средств в предприятие Пk, не зависит от вложения средств в другие предприятия; 2) доход, полученный от разных предприятий, выражается в одинаковых единицах; 3) общий доход равен сумме доходов, полученных от распределения всех средств по всем предприятиям. Определить, какое количество средств нужно выделить каждому предприятию, чтобы суммарный доход был максимальным. Запишем математическую постановку задачи. Суммарный доход определяется функцией Z = 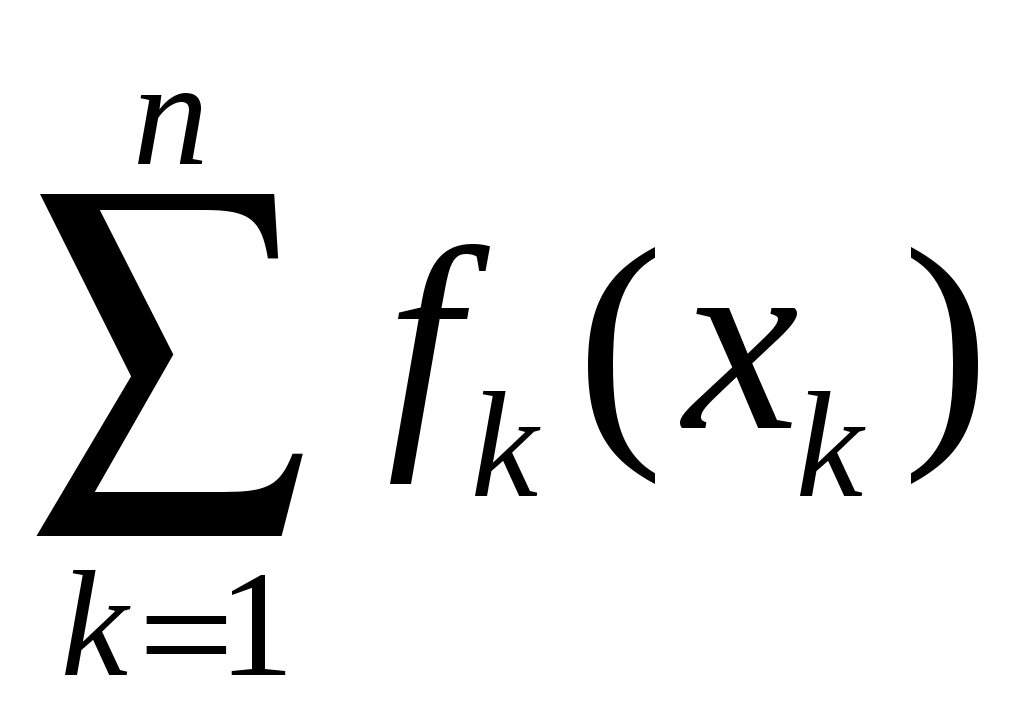 (*) (*)Переменные xkдолжны удовлетворять условиям x1 + x2 +…+ xn = 0 ; xk 0 (k=1,…,n) (**) Требуется определить переменные х\, ..., хп, которые удовлетворяют ограничениям (**) и обращают в максимум целевую функцию (*). Аналогичная задача оптимизации решалась в классическом анализе с помощью множителей Лагранжа. В прикладных задачах классический метод Лагранжа, как правило, неприменим по многим причинам и прежде всего — по причине размерности. Искать абсолютный максимум функции п переменных, даже если эта функция дифференцируема, дело трудоемкое. Если к тому же учесть, что экстремум может достигаться на границе, то к исследованию стационарных точек внутри области прибавляется исследование стационарных точек на ее границе. В практических задачах переменные xk могут принимать дискретные значения (например, средства выделяются в размерах, кратных 10 ед.), а функции дохода fk(xk) могут быть недифференцируемыми или даже заданными таблично. Во всех этих случаях классические методы оптимизации неприменимы. К решению задачи можно применить методы нелинейного программирования. Однако и они оказываются эффективными лишь при ряде дополнительных свойств функций fk(xk),которые на практике часто не выполняются. Наконец, иногда бывает важно не только получить решение конкретной задачи при определенных 0 и n, но и исследовать чувствительность решения к изменению этих исходных данных, что при использовании классических методов затруднительно. Покажем, как с помощью методов ДП указанные трудности легко преодолеваются. Перейдем к описанию задачи в виде модели ДП. Внутреннее свойство процесса распределения средств между п предприятиями позволяет рассматривать его как n-шаговый процесс. За номер k-гoшага примем номер предприятия, которому выделяются средства хk. На 1-м шаге выделяем 1-му предприятию средства х1,на 2-м шаге — 2-му предприятию выделяем средства х2из оставшихся и т. д. Очевидно, что переменные xk (k=1, ..., n)можно рассматривать как управляющие переменные. Начальное состояние системы характеризуется величиной o средств, подлежащих распределению. После выделения х1остается 1 = 0–x1 средств и т. д. Величины go, 1,2,…,n характеризующие остаток средств после распределения на предшествующих шагах, будем рассматривать как параметры состояния. Уравнениями состояния служат равенства k = k-1–xk (k=1, ..., n) (1.6) Суммарный доход за п шагов составляет Z = Ф (o ,U) = 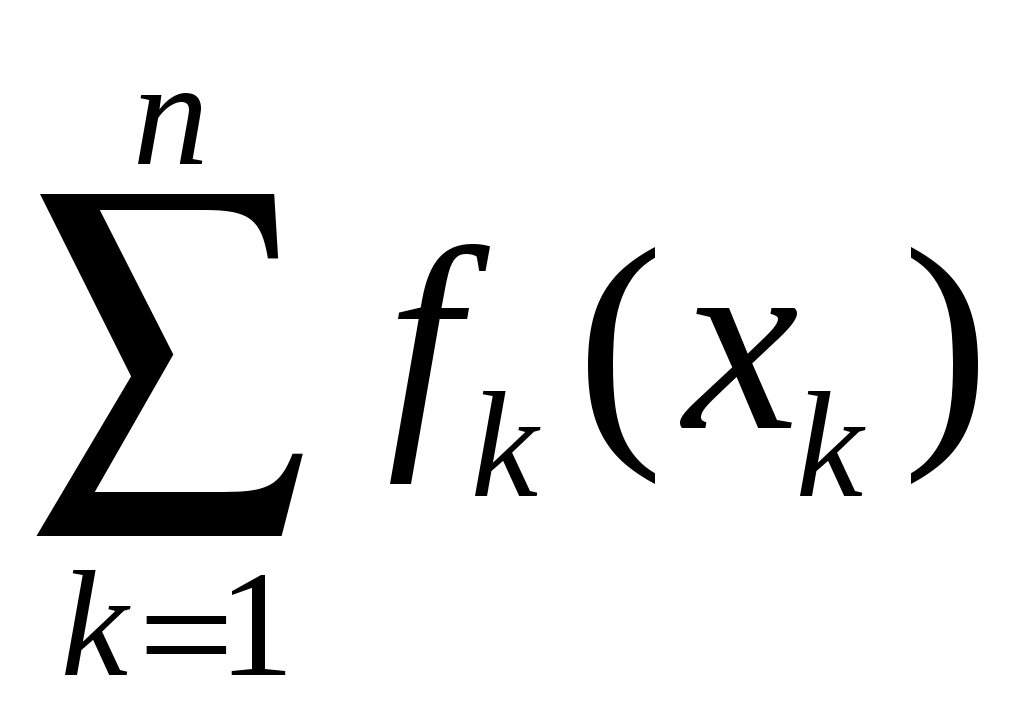 (1.7) (1.7)и представляет собой показатель эффективности процесса, имеющий, как видно из этого равенства, аддитивную форму. Если к началу k-гoшага остаток средств равен k-1 то доход, который можно получить на оставшихся n-k+1 шагах (т. е. от выделения средств предприятиям Пk, Пk+1, ..., Пn), составит Zk = 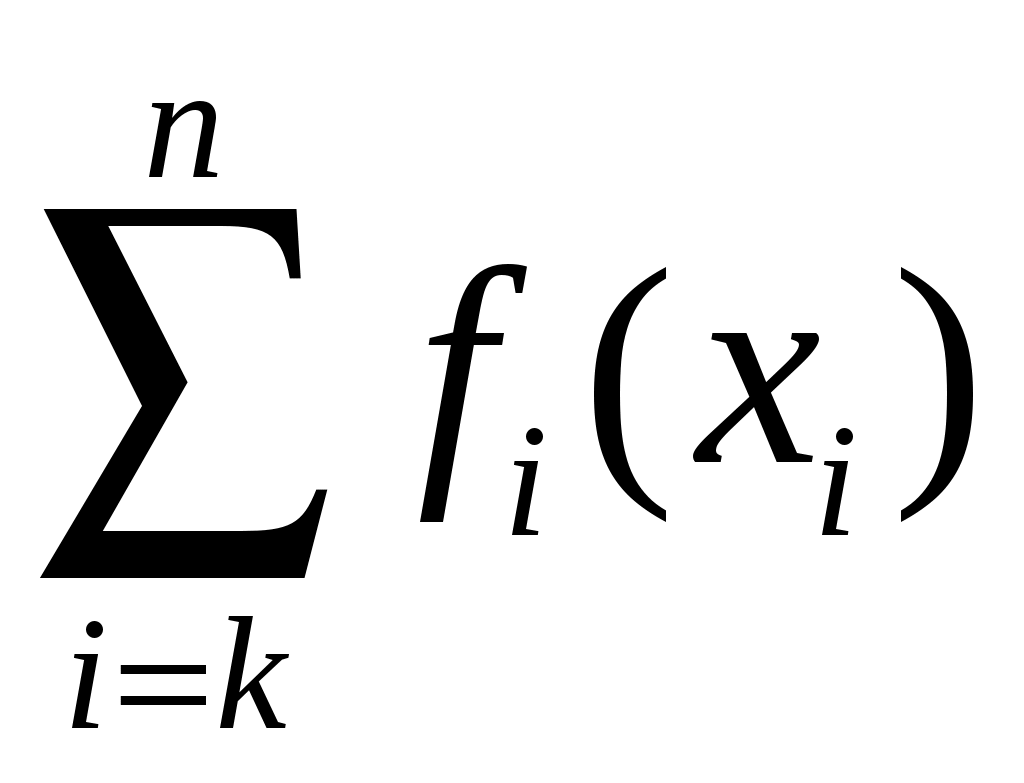 Максимальный доход за эти n-k+1шагов зависит от того, сколько средств осталось от предыдущих k-1 шагов, т. е. от величины k-1. Поэтому будем его обозначать через Zk*(k-1). Очевидно, что Z1*(0) =Zmax, т. е. Z1*(0) представляет собой суммарный максимальный доход за п шагов (доход, полученный при оптимальном распределении средств 0 между п предприятиями). Рассмотрим любой k-й шаг. Очевидно, что xkможно выбирать из условия 0 xk k-1 .Значение xk,удовлетворяющее этому двойному неравенству, называется допустимым. Принцип оптимальности в этом конкретном случае означает, что, выделив величину xkи получив от k-гoпредприятия доход fk(xk), мы должны распорядиться оставшимися средствами k = k-1–xkнаивыгоднейшим образом и получить от предприятий Пk+1, ..., Пn максимальный доход Zk+1*(k). Ясно, что величину xkследует определять из условия максимизации суммы fk(xk)+ Zk+1*(k). Таким образом, получаем уравнение Беллмана Zk*(k-1) = Перейдем к схеме вычислений. Нас интересует Z1*(0) , но если начать с 1-го шага, т.е. с решения задачи Z1*(0) = то необходимо знать Z2*(1). В свою очередь, при определении Z2*(1) нужно знать Z3*(2), и т. д. Однако имеется шаг, за которым нет последующих. Таким является n-й шаг, на котором выделяются средства последнему предприятию Пп. Для него равенство (1.8) имеет вид Zn-1*(n-1) = Будем считать, что функция дохода fn(xn)монотонно возрастает, поэтому решением этой задачи является условное оптимальное управление xn*(n-1) при котором достигается условный максимум Zn*(n-1) =fn(xn*). Следовательно, предприятию Пп выделяются все оставшиеся средства (n-1) , которые приносят доход fn(n-1). Вернемся к предыдущему, (n-1)-му шагу, в начале которого имеется остаток средств n-2 . Уравнение (1.8) в этом случае примет вид Здесь оптимальный выбор xn-1не столь очевиден, как при решении предыдущей задачи (1.9). Прежде всего, выразив из уравнения состояния n-1 через n-2- xn-1, получим Zn-1*(n-2) = Оба слагаемых в фигурных скобках — известные функции, зависящие от управляющей переменной xn-1.Параметр n-2 является начальным состоянием для данной задачи. Выполнив исследование на максимум функции Zn-1(xn-1,n-2) = fn-1(xn-1)+ Zn*(n-2- xn-1) от одной переменной xn-1 получим условное оптимальное управление xn-1*(n-2) и соответствующий условный максимум суммарного дохода Zn-1*(n-2). На языке данной задачи это решение означает, что если перед выделением средств предприятию Пn-1 в нашем распоряжении имеется остаток n-2,то предприятию Пn-1 необходимо выделить xn-1*(n-2) средств. При этом сумма доходов от предприятий Пn и Пn-1 достигает максимума. Закончив решение задачи (1.10), перейдем к следующему с конца (n-2)-му шагу, определим аналогичным образом условное оптимальное управление xn-2*(n-3) и соответствующий остатку n-3 условный максимум Zn-2*(n-3). В результате, проходя последовательно все шаги с конца процесса распределения к его началу (т. е. к 1-му шагу), получим две последовательности функций: Zn*(n-1), Zn-1*(n-2),…, Z2*(), Z1*(0) (условные максимальные доходы) и xn*(n-1), xn-1*(n-2),…, x2*(1), x1*(0) (условные оптимальные управления). Этим завершается первый и основной этап вычислительного процесса, получивший название условной оптимизации. Теперь приступаем ко второму этапу вычислительной схемы — безусловной оптимизации. На этом этапе, прежде всего, зная функцию Z1*(0), по заданному значению 0* определяем Zmax= Z1*(0*). Далее, обращаемся к последовательности xk*(k-1), которую проходим от начала к концу процесса. Выделяем x1*= x1*(0*) 1-му предприятию; тогда для распределения остается 1*= 0*- x1*. По этой величине определяем оптимальное количество средств х2* = х2*(1*), выделяемых 2-му предприятию. Снова находим 2*= 1*- x2*, после чего определяем х3*,ит. д., пока не будет определено искомое оптимальное управление (х1*, х2*,...,хn*). Пример. Решим задачу о распределении средств при заданных конкретных условиях. Тем самым на числовом примере продемонстрируем общую вычислительную схему Задача. Решить задачу 1 по следующим данным: 1) 0 = 200 млн. руб.; 2) п = 4; 3) средства выделяются только в размерах, кратных 40 млн. грн.; 4) функции дохода на каждом из четырех предприятий заданы в табл. 1: Таблица 1.
Условие 3) определяет дискретность задачи, а наличие на каждом шаге только одной переменной управления и одного параметра состояния показывают, что задача является одномерной. Учитывая это условие, можно было бы принять за единицу масштаба 40 млн. грн. Вследствие этого 0 = 5 ед. и возможные значения для управляющих переменных были бы равны 0, 1, 2, 3 и 4. Однако мы сохраним реальные единицы, в которых указаны исходные данные. В соответствии с обозначением § 3 имеем четыре управляющие переменные х1, х2, х3, х4и пять параметров состояния 0, 1, 2, 3, 4 . Уравнениями состояния служат следующие равенства: 1= - x1, 2= 1- x2, 3= 2- x3, 4= 3- x4 . (1.11) Уравнение Беллмана запишется в форме (1.8). Данный процесс является четырехшаговым. При этом, так как на последнем шаге (при k=5)процесс завершается и прибыль на «последующих» шагах отсутствует, то и Z5*(4)=0. Запишем уравнение (1.8) для последнего шага: Z4*(3) = и для всех предыдущих (k = 3, 2,1) шагов: Zk*(k-1) = Выражение, стоящее в фигурных скобках последнего равенства, обозначим через Zk(k-1,xk) = fk(xk)+ Zk+1*(k) (1.13) где к = к-1-хк. тогда уравнение Беллмана для любого шага запишется в виде Zk*(k-1) = Расчеты располагаем в двух таблицах – основной, в которой помещаем результаты условной оптимизации, т.е. последовательность функций Zk*(k-1) и xk*(k-1), и вспомагательной , в которой определяем Zk(k-1,хк) и выполняем условную оптимизацию. В основной таблице входом является параметр , для которого возможны значения 0,40,80,120,160 и 200 (см. табл.2) Таблица 2.(основная)
Условную оптимизацию начнем с расчета 4-го шага, для чего используем уравнение (1.12). Так как функция дохода f4(x4) монотонно возрастает (чем больше вкладывается средств, тем больше доход), то ее максимум достигается при наибольшем значении x4(3) = 3. При этом получим Z4*(3) = f4(3), где 0 3 200. Этот результат условной оптимизации 4-го шага помещаем непосредствено во 2-й и 3-й столбцы таблицы 2, переписав необходимые данные из последнего столбца таблицы 1. Условная оптимизация 3,2, и 1-го шагов выполняется сначала в таблице 3. Расчет ведется по формулам (1.13) и (1.14) при k =3, k =2, k =1. | |||||||||||||||||||||||||||||||||||||
