лабораторная 5. Лабораторная работа №5. Лабораторная работа Краткие теоретические сведения Метод множителей Лагранжа
 Скачать 306.02 Kb. Скачать 306.02 Kb.
|
|
Лабораторная работа № 5. Краткие теоретические сведения Метод множителей Лагранжа Метод множителей Лагранжа позволяет решить задачу оптимального управления, постановка которой в общем случае имеет вид: Уравнения движения объекта управления 𝑥̇𝑖 = 𝑓𝑖(𝐱, 𝐮, 𝑡), 𝑖 = 1, 2, … , 𝑛, где 𝐱 = (𝑥1 𝑥2 … 𝑥𝑛)𝑇 – вектор фазовых координат, 𝐮 = (𝑢1 𝑢2 … 𝑢𝑟)𝑇 – вектор управляющих переменных. Уравнения движения объекта управления должны быть приведены к дифференциальным уравнениям первого порядка, разрешенным относительно производных всех фазовых координат 𝑥𝑖. Таким образом, количество дифференциальных уравнений совпадает с количеством фазовых координат 𝑛. Ограничения 𝜑𝑘(𝐱, 𝐮, 𝑡) = 0, 𝑘 = 1, 2, … , 𝑙. Ограничения представляют собой алгебраические уравнения, кото рым должны удовлетворять фазовые и управляющие переменные. Ограничения могут отсутствовать (то есть 𝑙 = 0), если все процессы, протекающие в объекте управления, описаны с помощью дифференциальных уравнений. Граничные условия 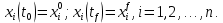 В задаче с фиксированными концами все фазовые координаты заданы в начальный 𝑡0 и конечный 𝑡𝑓 моменты времени. Таким образом, будет 2𝑛 граничных условий. В задаче с подвижным концом отсутствуют одно или несколько граничных условий и их будет меньше чем 2𝑛. В более общем случае граничные условия имеют вид 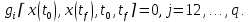 где 𝑞 ≤ 𝑛 – количество граничных условий. Критерий оптимальности 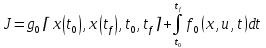 Критерий оптимальности в общем случае включает терминальное слагаемое 𝑔0 и интегральное. Терминальное слагаемое может присутствовать только в задаче с подвижным концом или нефиксированным временем, так как в задаче с закрепленными концами и фиксированным временем исключена вариация величин 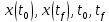 . .Алгоритм решения такой задачи включает следующие действия: Составить гамильтониан 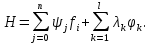 При 𝑙 = 0 вторая сумма отсутствует. Множитель Лагранжа 𝜓0 = −1. Составить уравнения Эйлера–Лагранжа 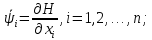 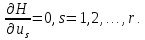 Последние уравнения называют условием стационарности. Выразить управляющие переменные 𝑢𝑠 (𝑠 = 1, 2, … , 𝑟) из условия стационарности и подставить в уравнения движения и уравнения Эйлера– Лагранжа. Получится система дифференциальных уравнений: 𝑥̇𝑖 = 𝑓𝑖(𝐱, 𝐮, 𝑡), 𝑖 = 1, 2, … , 𝑛; 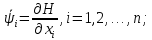 Решить данную систему уравнений с учетом граничных условий. В случае отсутствия некоторых граничных условий (задача с подвижным концом) записываются условия трансверсальности: 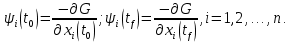 Для задачи с нефиксированным временем составляются условия трансверсальности, обусловленные вариацией начального или конечного момента времени: 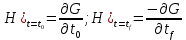 . .Количество граничных условий и условий трансверсальности должно совпадать с количеством постоянных интегрирования, то есть с количеством дифференциальных уравнений. Найти постоянные интегрирования. Подставить найденные постоянные интегрирования в выражения для 𝑥𝑖(𝑡) и 𝜓𝑖(𝑡), затем выразить 𝑢𝑗(𝑡) и записать в ответе оптимальные функции управления 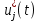 и функции переменных состояния и функции переменных состояния 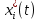 . Построить графики функций . Построить графики функций 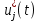 и и 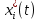 . . |
