лабораторная 5. Лабораторная работа №5. Лабораторная работа Краткие теоретические сведения Метод множителей Лагранжа
 Скачать 306.02 Kb. Скачать 306.02 Kb.
|
Пример выполнения лабораторной работы № 8Исходные данные: Исходные данные: Уравнения движения: 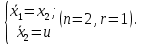 Ограничение : 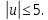 Граничные условия: Граничные условия:𝑥1(0) = 𝑥2(0) = 0, 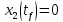 , 𝑡𝑓 = 10 с. , 𝑡𝑓 = 10 с.Критерий оптимальности в случае минимального расхода энергии управляющего воздействия равен: 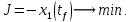 Решение:Гамильтониан 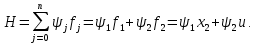 Уравнения Эйлера–Лагранжа 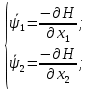 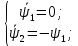 Решение данной системы уравнений с точностью до постоянных интегрирования: 𝜓1 = 𝐶1, 𝜓2 = −𝐶1𝑡 + 𝐶2. Условие принципа максимума: max 𝐻 = max(𝜓1𝑥2 + 𝜓2𝑢) = 𝜓1𝑥2 + max(𝜓2𝑢). |𝑢|≤5 |𝑢|≤5 |𝑢|≤5 Из условия принципа максимума следует, что 𝑢 = 5sign(𝜓2). То есть принимает значение 5 или –5 в зависимости от знака функции 𝜓2 = −𝐶1𝑡 + 𝐶2. Так как функция 𝜓2 линейная, то она может изменить знак только один раз и может быть только одна точка переключения. Обо- значим момент переключения 𝑡1. Возможно два варианта: 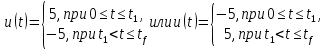 Далее необходимо полностью выполнить решение для обеих гипотез и выбрать ту из них, для которой ответ получится оптимальным. Для начала рассмотрим первую гипотезу: 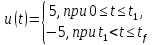 Найдем решение системы уравнений движения для двух участков а) Первый участок 0 ≤ 𝑡 ≤ 𝑡1, 𝑢 = 5. 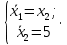 С учетом граничных условий в начальный момент времени 𝑥1(0) = 𝑥2(0) = 0 решение данной системы дифференциальных уравнений будет следующим: 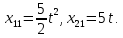 б) Второй участок 𝑡1 < 𝑡 ≤ 𝑡𝑓, 𝑢 = −5. 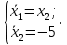 С учетом граничного условия в конечный момент времени 𝑥2(10) = 0 решение данной системы дифференциальных уравнений будет иметь одну произвольную постоянную: 𝑥12 = 𝐶 + 𝑡(50 − 5𝑡), 𝑥22 = 50 − 5𝑡. Для определения постоянной 𝐶 и времени переключения 𝑡1 запишем условия неразрывности: 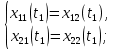 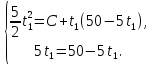 Решив данную систему уравнений, получим: 𝑡1 = 5 c, 𝐶 = −125. Таким образом, оптимальные управляющая переменная и пере менные состояния будут равны: 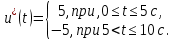 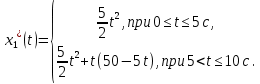 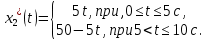 Графики функции управления 𝑢∗(𝑡) и переменных состояния 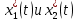 представлены на рис. 8.1. Контрольные вопросы к лабораторной работе № 8В чем суть принципа максимума? Что общего с методом множителей Лагранжа и в чем отличие? В каких случаях следует применять принцип максимума Понтрягина? Расскажите алгоритм решения задачи оптимального управления с помощью принципа максимума Понтрягина. Чему равен критерий оптимальности в задаче? Как записать критерий оптимальности исходя из условий задачи? Классифицируйте задачу, решаемую в лабораторной работе. Как составляется условие максимума? Для чего оно используется? Как составляется условие неразрывности? Для чего оно используется? 
5  u* 0 -5 0 1 2 3 4 5 6 7 8 9 10 t, с 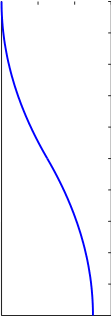 150 150100  x * 1 50 0 0 1 2 3 4 5 6 7 8 9 10 t, с 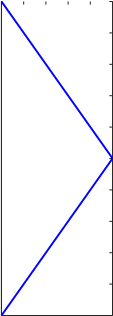 25 2520 15  x * 2 10 5 0 0 1 2 3 4 5 6 7 8 9 10 T, c Рис. 8.1. Зависимости управления 𝑢∗(𝑡) и переменных состояния 𝑥1 ∗(𝑡), 𝑥2 ∗(𝑡) от времени  |
