лабораторная 5. Лабораторная работа №5. Лабораторная работа Краткие теоретические сведения Метод множителей Лагранжа
 Скачать 306.02 Kb. Скачать 306.02 Kb.
|
Пример выполнения лабораторной работы № 6Исходные данные: Уравнения движения: 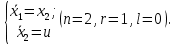 Граничные условия: Граничные условия:𝑥1(0) = 𝑥2(0) = 0, 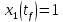 , 𝑡𝑓 = 1 с. , 𝑡𝑓 = 1 с.Критерий оптимальности в случае минимального расхода энергии управляющего воздействия равен: 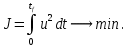 Решение:Гамильтониан 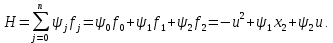 Уравнения Эйлера–Лагранжа 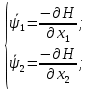 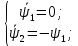 Условие стационарности 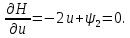 Из условия стационарности выразим 𝑢 = 𝜓2⁄2. Подставив 𝑢 в уравнения движения и уравнения Эйлера–Лагранжа, получим систему уравнений 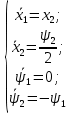 Решение данной системы дифференциальных уравнений с учетом трех имеющихся граничных условий имеет вид: 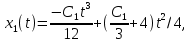 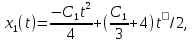 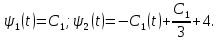 Для поиска постоянной 𝐶1 запишем условие трансверсальности: 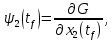 где 𝐺 = 𝑔0 = 0, так как в критерии оптимальности отсутствует терми нальное слагаемое. Таким образом, 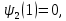 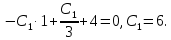 Подставив найденные постоянные в выражения для 𝑥𝑖(𝑡) и 𝜓𝑖(𝑡), получим 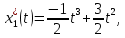 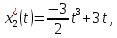 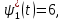 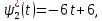 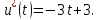 Графики функции управления 𝑢∗(𝑡) и переменных состояния 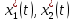 представлены на рис. 6.1. представлены на рис. 6.1. 3 32  u* 1 0 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 t, с  
1 0.8  1 0.6  x 0.4 02 0 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 t, с  
1.5 1   x 2 0.5 0 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 t, с Рисунок. 6.1.Зависимости управления 𝑢∗(𝑡) и переменных состояния 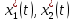 от времени от времени |
