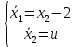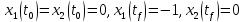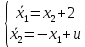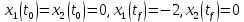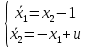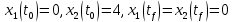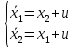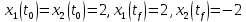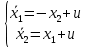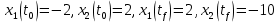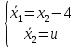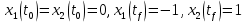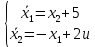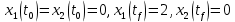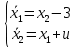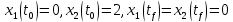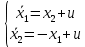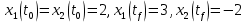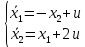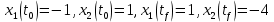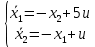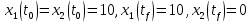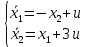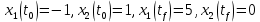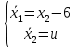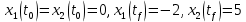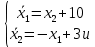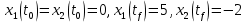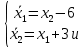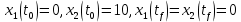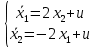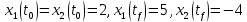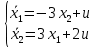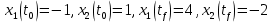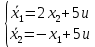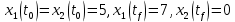лабораторная 5. Лабораторная работа №5. Лабораторная работа Краткие теоретические сведения Метод множителей Лагранжа
 Скачать 306.02 Kb. Скачать 306.02 Kb.
|
Метод Эйлера–Лагранжа: задача с фиксированными концамиЗаданиеРешите задачу оптимального управления: перевести объект управления, уравнения движения которого заданы, в заданное положение при минимальном расходе энергии управляющего воздействия. Начальный момент времени 𝑡0 = 0. Уравнения движения, граничные условия и конечное время 𝑡𝑓 заданы в табл. 5.1 по вариантам. Постройте графики 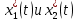 и график функции управления 𝑢∗(𝑡). и график функции управления 𝑢∗(𝑡).Пример выполнения лабораторной работы № 5 Исходные данные: Уравнения движения: 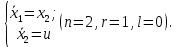 Граничные условия: Граничные условия: 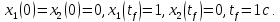 Критерий оптимальности в случае минимального расхода энергии управляющего воздействия равен: 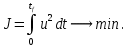 Решение:Гамильтониан 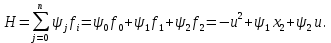 Уравнения Эйлера–Лагранжа 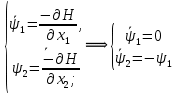 Условие стационарности 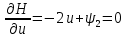 Из условия стационарности выразим 𝑢 = 𝜓2⁄2. Подставив 𝑢 в уравнения движения и уравнения Эйлера-Лагранжа, получим систему уравнений Решение данной системы дифференциальных уравнений имеет вид 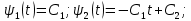 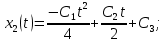 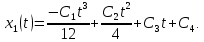 Данное решение содержит четыре постоянных интегрирования: 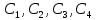 , которые можно найти, используя граничные условия: , которые можно найти, используя граничные условия: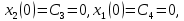 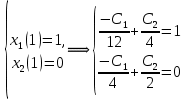 откуда 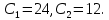 . .Подставив найденные постоянные в выражения для 𝑥𝑖(𝑡) и 𝜓𝑖(𝑡), получим  1 𝑥∗(𝑡) = −2𝑡3 + 3𝑡2;  2 𝑥∗(𝑡) = −6𝑡2 + 6𝑡;  1 𝜓∗(𝑡) = 24;  2 𝜓∗(𝑡) = −24𝑡 + 12; 𝑢∗(𝑡) = −12𝑡 + 6. Графики функции управления 𝑢∗(𝑡) и переменных состояния 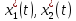 представлены на рис. 6.1. представлены на рис. 6.1.Таблица 5.1 Исходные данные к лабораторной работе № 5 Задание №1.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||