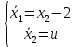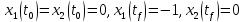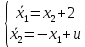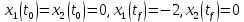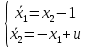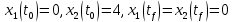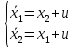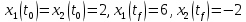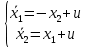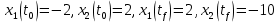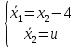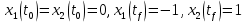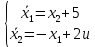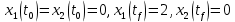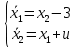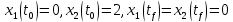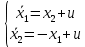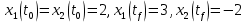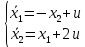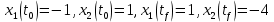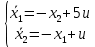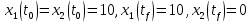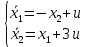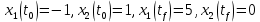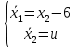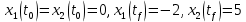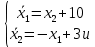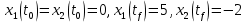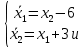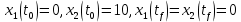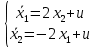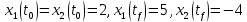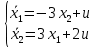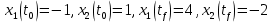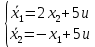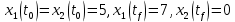лабораторная 5. Лабораторная работа №5. Лабораторная работа Краткие теоретические сведения Метод множителей Лагранжа

• Название: Лабораторная работа Краткие теоретические сведения Метод множителей Лагранжа
• Анкор: лабораторная 5
• Дата: 05.12.2021
• Размер: 306.02 Kb.
• Имя файла: Лабораторная работа №5.docx
• Тип: Лабораторная работа; #292270
• страница: 6 из 9

Контрольные вопросы к лабораторной работе № 6

1. 
   Расскажите алгоритм решения задачи оптимального управления с помощью метода множителей Лагранжа.
   
2. 
   Чему равен критерий оптимальности в задаче? Как записать критерий оптимальности исходя из условий задачи?
   
3. 
   Классифицируйте задачу, решаемую в лабораторной работе.
   
4. 
   Чем отличаются решения задач с закрепленными концами и с подвижным концом?
   
5. 
   Как составляются уравнения Эйлера–Лагранжа? Для чего используются эти уравнения?
   
6. 
   Как составляется условие стационарности? Для чего оно используется?
   
7. 
   Как записываются условия трансверсальности? Для чего они ис пользуются?
   
8. 
   Как определяются постоянные интегрирования в задаче с подвиж ным концом?
   
9. 
   Расскажите о назначении команд Matlab: syms, clc, clear, for.
   
10. 
    Расскажите о назначении функций Matlab: solve, dsolve, diff, subs, eval, plot. Какие аргументы принимают и что возвращают эти функции?
    

Лабораторная работа № 7.

Метод Эйлера–Лагранжа: задача с изопериметрическим ограничением

Решите задачу оптимального управления: перевести объект управления, уравнения движения которого заданы, в заданное положение за минимальное время при изопериметрическом ограничении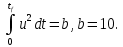



Начальное время 𝑡₀ = 0. Уравнения движения, граничные условия заданы в табл. 7.1. по вариантам.

Постройте графики 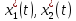и график функции управления 𝑢^∗(𝑡).

Таблица7.1.

Исходные данные к лабораторной работе № 7

Задание 1.

Вариант	Уравнения движения	Граничные условия
1
2
3
4
5
6
7
8
9
Задание 2.
1
2
3
4
5
6
7
8
9