метрология. Контрольная работа Метрология для заочников. Методические указания и задания к контрольной работе для студентов заочной формы обучения
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
3.2. Обработка данных при прямых многократных измеренияхПри прямых измерениях с многократными наблюдениями ставится задача оценивания результата измерения и уточнения случайных составляющих погрешности этого результата. Для обработки данных используют статистические методы, при этом подразумевается, что производится многократное наблюдение величины, которая за период наблюдения не изменяется или ее изменения лежат в диапазоне случайного разброса. Результатом многократного измерения является среднее арифметическое n отдельных независимых наблюдений, составляющих массив экспериментальных данных X1, Х2, ... ,Xi... Хn: 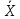 = = 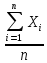 . .Приведенное 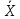 является оценкой среднего значения результата измерения, так как точного знания этого результата измерения получить невозможно из-за ограниченного объема экспериментальных данных. является оценкой среднего значения результата измерения, так как точного знания этого результата измерения получить невозможно из-за ограниченного объема экспериментальных данных.Среднее квадратическое отклонение (СКО) результата многократного измерения определяется зависимостью: σ = 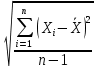 , а для среднего арифметического результата измерения: , а для среднего арифметического результата измерения: 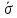 = = 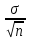 . Абсолютная ошибка измерений составит ∆ = . Абсолютная ошибка измерений составит ∆ = 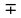 tα∙ tα∙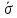 , относительная ошибка – δ = , относительная ошибка – δ = 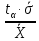 ∙100%, где tα - коэффициент Стьюдента, определяемый доверительной вероятностью α. ∙100%, где tα - коэффициент Стьюдента, определяемый доверительной вероятностью α.Рассмотрим пример обработки массива экспериментальных данных (табл. 2) . В таблице приведены 15 наблюдений при измерении температуры Tiв °С. Таблица 2 - Экспериментальныеданныенаблюдениятемпературы
Согласно априорной информации, систематических составляющих погрешностей нет, а разброс наблюдений подчиняется нормальному закону распределения вероятностей. Тогда параметры наблюдений температуры составят: 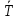 = 20,404°С, σ = 0,033 = 20,404°С, σ = 0,033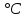 , , 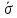 = 0,008 = 0,008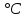 . Рассчитаем оценку случайной составляющей погрешности с доверительной вероятностью Рα =0,997 (tα = 3), получим: ∆ = . Рассчитаем оценку случайной составляющей погрешности с доверительной вероятностью Рα =0,997 (tα = 3), получим: ∆ = 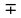 tα∙ tα∙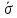 = 3∙0,008 = 0,024 = 3∙0,008 = 0,024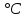 , т. е. после округления результат измерения температуры можно представить в одном из двух вариантов: , т. е. после округления результат измерения температуры можно представить в одном из двух вариантов: 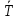 = 20,40 °С; ∆ = ±0,02°С; Рα = 0,997 или = 20,40 °С; ∆ = ±0,02°С; Рα = 0,997 или 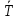 = (20,40 ± 0,02)°С; Рα = 0,997, относительная ошибка - δ = = (20,40 ± 0,02)°С; Рα = 0,997, относительная ошибка - δ = 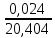 ∙100% ∙100% 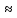 0,1%. 0,1%.Задание По экспериментальным данным (приложение 2) многократных наблюдений при прямом измерении параметра X, вычислить результат измерения - 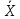 и его случайную составляющую погрешности ∆, при Pα = 0,68 (tα = 1), Pα = 0,95 (tα = 2), Pα = 0,997 (tα = 3). и его случайную составляющую погрешности ∆, при Pα = 0,68 (tα = 1), Pα = 0,95 (tα = 2), Pα = 0,997 (tα = 3). |

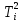 ∙10-6
∙10-6