метрология. Контрольная работа Метрология для заочников. Методические указания и задания к контрольной работе для студентов заочной формы обучения
 Скачать 0.63 Mb.
|
2. Рекомендации по выполнению и оформлениюконтрольной работы Студенты выполняют контрольную работу, в которой нужно выполнить расчетные задания. Номерварианта студент выбирает по двум последним цифрам шифра.Прежде чем приступить к выполнению контрольной работы, студенту необходимо изучить соответствующий материал по литературным источникам и получить полное представление по рассматриваемым темам дисциплины. Контрольная работа выполняется на сброшюрованных листах формата А4 в рукописном и печатном виде. Текст вопроса переписывается полностью под тем же номером. Ответ на вопрос помещается под текстом вопроса. Рисунки выполняются крупно (лучше на отдельной странице), с помощью чертежных инструментов, с указанием всех размеров, числовых данных и осей координат или с применением копировальных устройств. Все необходимые расчеты должны проводиться с точностью до 0,01 в системе СИ. В формулах в качестве символов следует применять обозначения, установленные соответствующими государственными стандартами. Пояснения символов и числовых коэффициентов, входящих в формулу, если они не пояснены ранее в тексте, должны быть приведены непосредственно под формулой. Пояснения каждого символа следует давать с новой строки в той последовательности, в которой символы приведены в формуле. Таблицы оформляются в соответствии с ГОСТ 2.105-95 "Единая система конструкторской документации. Общие требования к текстовым документам". Исправления работы после проверки преподавателем записываются в конце на чистых листах (а не в тексте решения). К работе, предоставляемой на повторную проверку, в обязательном порядке должен прилагаться ее первоначальный (незачтенный) вариант. 3. Задания контрольной работы3.1. Градуировка средств измеренийСредствами измерений (СИ) являются измерительные технические устройства, имеющие нормированные метрологические характеристики. Под метрологическими характеристиками понимают такие свойства СИ, которые позволяют оценить результат измерения физических величин и его погрешности. Техническое средство непосредственно после изготовления становится измерительным после передачи ему единицы (или шкалы) от другого более точного СИ. Эта операция называется градуировкой, что означает определение функциональной зависимости между входной (в частности, измеряемой физической величиной) и выходной величинами с использованием образцовых СИ на входе и выходе этого СИ. Градуировка выполняется в условиях, когда измеряемая величина либо не меняется, либо ее изменением можно пренебречь, а время позволяет снимать показания после того, как указатель отсчетного устройства окончательно остановится на какой-нибудь отметке шкалы. Различают градуировку в отдельных точках диапазона измерений и построение непрерывной градуировочной характеристики. Градуировка в отдельных точках диапазона измерений является наиболее простой. Так, например, при градуировке ртутного термометра в двух реперных точках (при температуре таяния льда и температуре кипения воды) получают по n значений длины ртутного столба в каждой точке. Затем в центрах рассеяния наносят отметки шкалы и присваивают этим отметкам значения 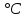0  и 100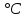 , соответственно. Если длина ртутного столба прямо пропорциональна измеряемой температуре, то расстояние между полученными отметками шкалы можно разбить на 100 равных частей и получить термометрическую шкалу с ценой деления 1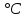 .Построение градуировочной характеристики предполагает две возможности. Первая из них заключается в том, что зависимость между входным воздействием и откликом на него известна (например, линейная, квадратичная, логарифмическая и т.п.), но неизвестны коэффициенты, входящие в соответствующее алгебраическое уравнение. Вторая возможность состоит в необходимости аппроксимации экспериментальных данных аналитической зависимостью. Если вид градуировочной характеристики Y = f(X),где X- входная величина, Y- выходная величина, то задача состоит в том, чтобы в её представлении полиномом соответствующей степени: Y = a0 + a1∙X + a2∙X2 +…+ am∙Xm найти такие значения коэффициентов a0, a1, a2,…,am, при которых эта зависимость наилучшим образом соответствовала бы экспериментальным данным. На рис. 1 показаны некоторые варианты построения линейной градуировочной характеристики по экспериментальным данным, обозначенным кружочками. Вопрос о том, какой из вариантов лучше, должен решаться на основе определенного критерия. Если значения входных воздействий X1, X2,...,Xnизвестны точно, а отклики на них Y1,Y2, …,Ynподчиняются нормальному закону распределения вероятности, то обычно используется метод наименьших квадратов (МНК). 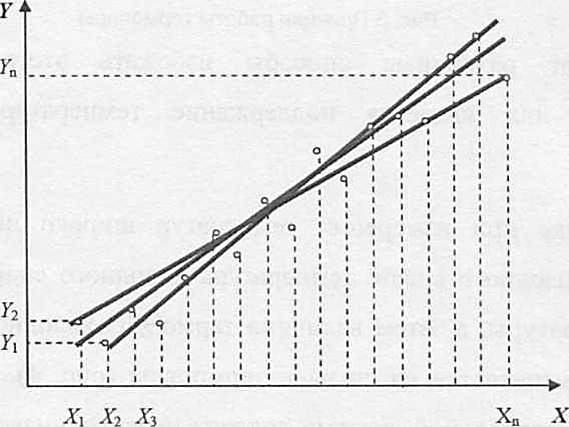 Рисунок 1 - Построение линейной градуировочной характеристики по экспериментальным данным Минимизируется сумма квадратов отклонений откликов по оси ординат от градуировочной характеристики: 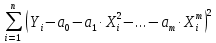 = min.Коэффициенты a0, al, a2,..., аm, определяющие оптимальную по критерию наименьших квадратов градуировочную характеристику, находятся из условия равенства нулю производных от этой суммы по каждому коэффициенту. Пример При градуировке измерительного прибора с линейной градуировочной характеристикой получены числовые значения экспериментальных данных, представленные в табл. 1. Таблица 1 - Экспериментальные данные
Найти методом наименьших квадратов аналитическое выражение для градуировочной характеристики и построить её графически. Решение: Линейная градуировочная характеристика описывается выражением: Y= а0 + а1∙X, где коэффициенты а0и a1 методом наименьших квадратов находятся по формулам: a0= 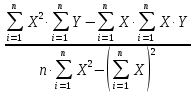 ,a1= 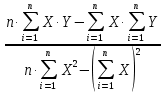 .В рассматриваемом случае а0= 0,7; а1 = 0,124, так что аналитическое выражение для градуировочной характеристики имеет вид: Y= 0,7 + 0,124 X. Графически она построена на рис. 2, где точками нанесены экспериментальные данные. 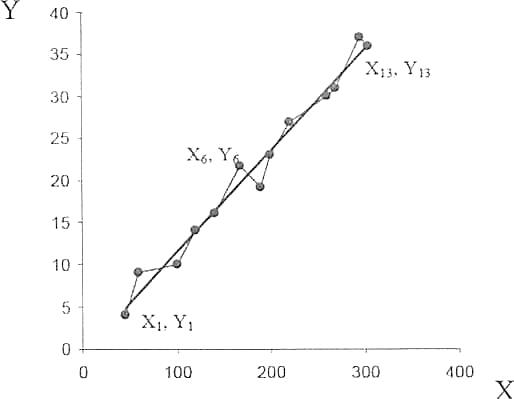 Рисунок 2 - Градуировочная характеристика Выражениями для a0 и a1, полученными в рассмотренном примере, можно пользоваться при градуировке измерительных приборов с нелинейными градуировочными характеристиками.Так, например, если она описывается зависимостью: Y= a0+ 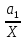 , то в формулы для коэффициентов a0 и a1 вместо X следует подставлять Z = 1/X, точно так же, если Y= а0 + а1∙X2, то задача линеаризуется подстановкой Z = X 2 .Иногда для линеаризации может использоваться логарифмирование. Если, например Y = a0∙ 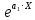 , то после логарифмирования по основанию натуральных логарифмов получается: lnY = lna0 + a1∙X.Если градуировочная характеристика СИ имеет вид: Y = k0∙ 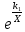 , то после логарифмирования выражения получим:lnY = lnk0+ 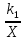 . Произведя замену переменных, составим линейное уравнение относительно новых переменных: Z = a0 + a1∙W, где Z= lnY,a0 = lnk0,а1 = k1∙W= X-1.Для линеаризации градуировочной характеристики СИ вида: Y = k0∙ln 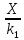 представим выражение в виде:Y =k0∙(lnX – lnk1),oтсюда:Y= k0∙lnX - k0∙lnk1, и получим линейную зависимостьY= а0 + а1∙Z, гдеа0 = -k0∙lnk1; а1= k0;Z = lnX. Если вид характеристики неизвестен, то возникает задача отыскания наилучшей аппроксимации экспериментальных данных, полученных при градуировке, аналитической зависимостью (рис. 3). 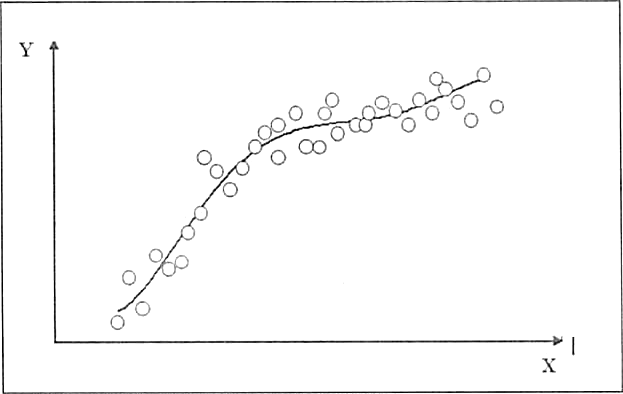 Рисунок 3 - Построение градуировочной характеристики, вид которой неизвестен Решение ее методом наименьших квадратов (МНК) отличается от решения предыдущей задачи только тем, что степень полинома Y = a0 + a1∙X + a2∙X2 +… неизвестна. Она устанавливается на основании требований к точности градуировки. Количество уравнений для определения коэффициентов a0, a1, a2,...всегда равно числу неизвестных, так что задача имеет единственное решение. Задание При градуировке средства измерения с линейной функциональной характеристикой получены числовые значения экспериментальных данных, приведенные в приложении 1. По полученным данным найти методом наименьших квадратов аналитические выражения для градуировочной характеристики и построить ее графически. |