Гидравлика_практ. Методические указания к индивидуальному домашнему заданию по дисциплине механика жидкостей и газов Волгодонск 2012 г
 Скачать 3.03 Mb.
|
|
Пример расчета. Задача 3. 3.1 Определение напора  Расчетные схемы 1,2. Определить напор , необходимый для пропуска расхода через гидравлический короткий трубопровод заданных размеров с эквивалентной шероховатостью труб  =0,5 мм. Угол закрытия пробкового крана  . Построить напорную и пьезометрическую линии.Решение. Запишем уравнение Бернулли в общем виде для двух выбранных сечений 1-1 и 2-2 относительно плоскости сравнения 0-0:  .Для обоих схем (см. бланк задания):   ;  ;  ;  ;  Для расчетной схемы 1  ,для схемы 2 -  .После подстановки выражений в уравнение Бернулли получим при свободном истечении (схема 1):  ,т.е. весь напор расходуется на преодоление всех сопротивлений и создание скоростного напора на выходе.Для случая затопленного истечения на выходе (схема 2) получим:  ,т.е. весь напор расходуется на преодоление всех сопротивлений (равен сумме всех потерь напора). Суммарные потери напора запишутся в соответствии со схемой трубопровода, используя формулу (3.1). Потери напора по длине (на трение) в первой и во второй трубах определяются по формуле (3.9), предварительно подсчитав скорости  и  по фомуле (3.7) и числа Рейнольдса  и  , и установив область сопротивления для выбора расчетной формулы  .Обоснование расчетной формулы для коэффициентов Дарси  и  в обоих трубах начать с проверки соответствия квадратичной области сопротивления в виде соотношения (3.15). При невыполнения условия (3.15), перейти к проверке соответствия потерь напора доквадратичной области сопротивления по зависимости (3.13) и т.д.Местные потери подсчитываются по формуле Вейсбаха (3.17), причем, коэффициенты местных сопротивлений принимаются равными  =0,5,  =1,0), а для других сопротивлений подсчитываются по формулам (2.18), (2.19) или принимаются по табличным данным, выше.Суммируя все потери напора для схем 1 и 2, получим: для схемы 1  для схемы 2  Построение напорной и пьезометрической линий На миллиметровке в выбранных вертикальном и горизонтальном масштабах вычерчивается короткий трубопровод (диаметр показывается в условном масштабе - схематично), откладывается рассчитанная величина напора .Откладывая потери напора на вход  от начального положения линии Е-Е и далее последовательно все потери по длине и местные с учетом их расположения, строится напорная линия. Ниже этой линии, на расстоянии равном величине скоростных напоров  и  , для каждой трубы строится пьезометрическая линия Р-Р. Пример построения линий показан на рисунке 3.2. Рисунок 3.2 - Построение напорной и пьезометрической линий для схемы 1 При свободном истечении на выходе (схема 1) пьезометрическая линия приходит в конце трубы к центру выходного сечения, а линия Е-Е рас-полагается выше на величинy удельной кинетической энергии , которой обладает поток на выходе.Для случая затопленного истечения (схема 2) линия Р-Р и Е-Е на выходе приходят к уровню воды в баке (нижнем бьефе сооружений), так как величина скоростного напора в баке (сечение 2-2) незначительна и была принята в расчете равной нулю. 3.2 Определение расхода  Определить расход, подаваемый из водохранилища в канал с помощью сифонного водовыпуска (схема 3) или проходящий через трубу дюкера (схема 4) заданных размеров при расчетном напоре .Дюкер - водопроводящее сооружение, которое устраивается на каналах в местах его пересечения с различными препятствиями (река, дорога, другой канал, овраг и др.). Решение. Для решения задачи необходимо записать уравнение Бернулли для двух сечений 1-1 и 2-2 относительно плоскости сравнения 0-0 (схемы 3 и 4), после преобразования которого получим: .Выражая потери напора по длине и местные по формулам (3.9), (3.17) и учитывая, что величина  получим зависимость для определения скорости, по известным коэффициентам сопротивления, и далее определяем расход по формуле (3.6). ПРИМЕЧАНИЕ: Вычисление расхода воды, проходящего через сифонный водовыпуск или дюкер, ведется в табличной форме (таблица 3.1) методом последовательного приближения в следующей последовательности: 1. Определяются коэффициенты местных сопротивлений для заданного трубопровода. Согласно справочным данным [7-9] и по таблицам приложения. 2. Предполагаем вначале, что потери напора по длине отвечают квадратичной области сопротивления, при которой потери не зависят от числа  , а коэффициент может определяться по формуле (3.16) Шифринсона (3.16) - первое приближение.3. Определяем среднюю скорость в трубе. 4. Для проверки соответствия, принятой в первом приближении квадратичной области сопротивления, подсчитываются число ,  и  . Если окажется , что  , то предположение о том, что область сопротивления квадратичная, подтвердилось, и тогда первое приближение является окончательным и последующие приближения не нужны.Расход воды определяется по основной формуле (3.6). 5. Если окажется, что  , то расчет ведется для доквадратичной области сопротивления по числу , полученному расчетами в первом приближении - второе приближение. Коэффициент определяется по формуле А.Д. Альтшуля (3.14). Далее подсчитывается  и . Сравнивая с и , устанавливается соответствие доквадратичной области сопротивлений. При подтверждении доквадратичной области, подсчитывается расход и дальнейший расчет в третьем приближении не ведется.6. Если  , необходимо продолжить расчет для области сопротивления, отвечающей гидравлически гладким руслам - третье приближение. Расчет ведется по аналогии с предыдущими приближениями.Таблица 3.1
Примечание: *) Расход подсчитывается, если область сопротивления подтверждена. Для построения напорной и пьезометрической линий с помощью расчетных зависимостей Вейсбаха (3.17) и Дарси-Вейсбаха (3.9) подсчитываются потери напора 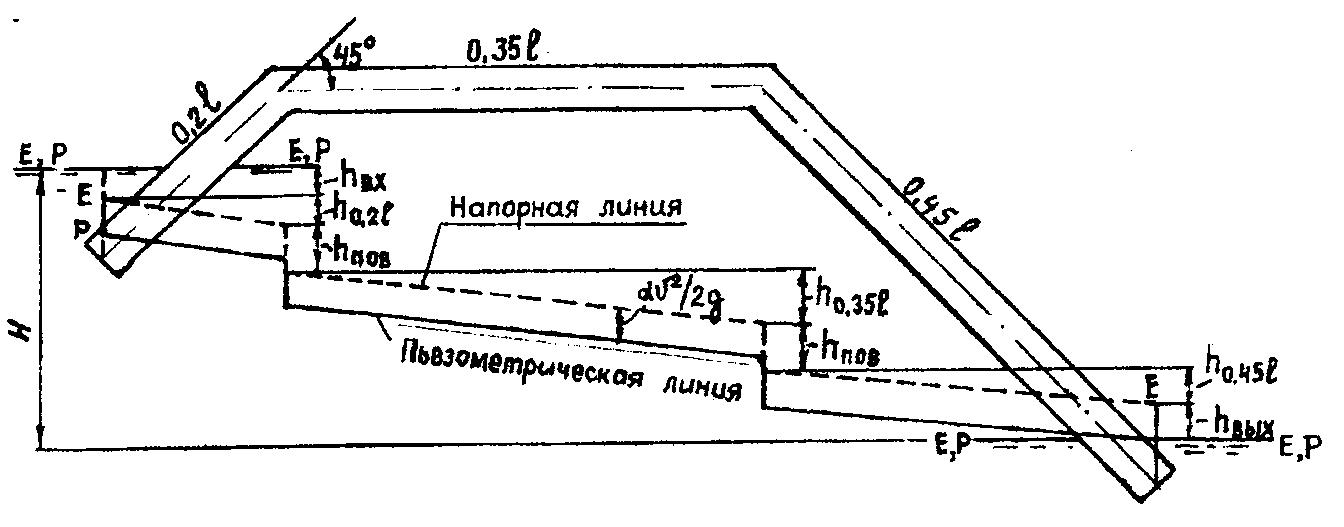,  ,  ,  . Порядок построения линий Е-Е и Р-Р изложен ранее, а для схемы 3, в качестве примера, показан на рисунке 3.2. Рисунок 3.2 - Построение напорной и пьезометрической линий для сифона 3.3 Определение диаметра трубопровода Определить диаметр сифонного водовыпуска (схема 3) или дюкера (схема 4), необходимого для пропуска расчетного расхода при заданных длине трубы, напоре .Решение. Записать уравнение Бернулли для двух сечений 1-1 и 2-2 относительно плоскости сравнения 0-0, показанных для схем 3,4. После расшифровки каждого члена уравнения и преобразований получим:  .Выражая суммарные потери  по зависимостям (3.1), (3.9), (3.17) и учитывая, что величина , получим формулу для определения , в которой две неизвестных величины - диаметр и средняя скорость в трубе. Искомый диаметр сифона, дюкера определяется методом подбора.ПРИМЕЧАНИЕ: Вычисление искомого диаметра сифона, дюкера определяется методом подбора. Расчет ведется в табличной форме (таблица 3.2) методом последовательного приближения в следующей последовательности: 1. Определяются коэффициенты местных сопротивлений. 2. Задаются рядом значений диаметра трубы. 3. Для каждого размера определяется средняя скорость, число Рейнольдса, область сопротивления, коэффициент гидравлического трения и суммарные потери напора  .Таблица 3.2
Примечание: *) Если будут больше расчетного напора , то в следующейстроке (подборе) необходимо увеличить  , если < - диаметр уменьшить.4. По данным таблицы 3.2 строится график зависимости 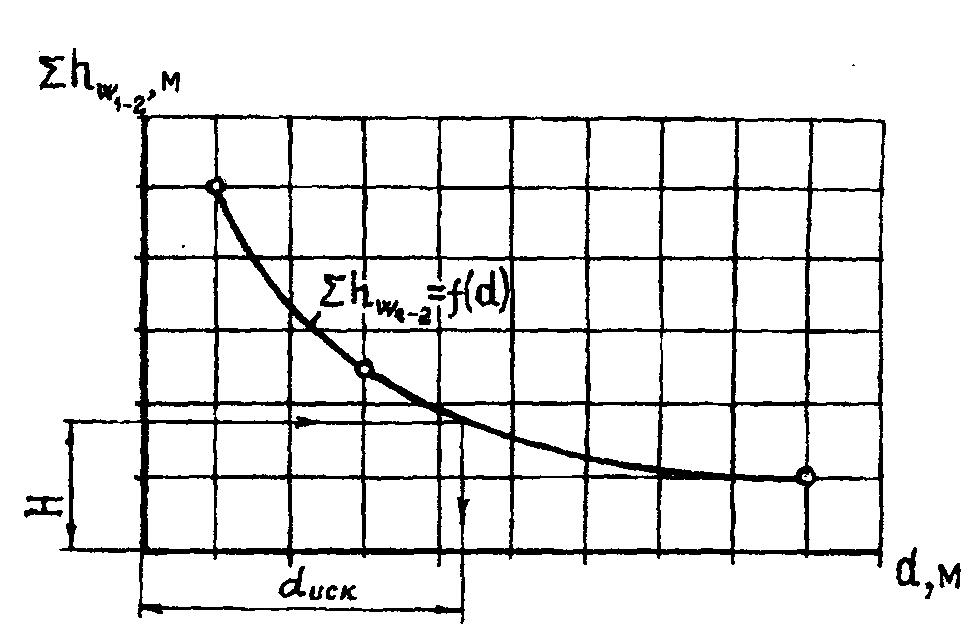 , как показано на рисунке 3.3, с помощью которого по расчетному напору (из бланка задания) определяется искомый диаметр сифона или дюкера. Рисунок 3.3 - График зависимости Для построения напорной и пьезометрической линий по определившемуся диаметру трубы подсчитываются: 1. Средняя скорость воды в трубе 2. Местные потери напора по формуле Вейсбаха (3.17). 3. Коэффициент гидравлического трения: для определения коэффициента подсчитываются число Рейнольдса,  и ; сравнивается с и ; устанавливается область сопротивления и выбирается расчетная формула для .4. Потери напора по длине по формуле Дарси-Вейсбаха (3.9) Порядок построения линий полной энергии и пьезометрической приведен в п. 3.1. Пример построения линий Е-Е и Р-Р показан на рисунке 3.2. |
,