Гидравлика_практ. Методические указания к индивидуальному домашнему заданию по дисциплине механика жидкостей и газов Волгодонск 2012 г

• Название: Методические указания к индивидуальному домашнему заданию по дисциплине механика жидкостей и газов Волгодонск 2012 г
• Анкор: Гидравлика_практ.doc
• Дата: 15.12.2017
• Размер: 3.03 Mb.
• Имя файла: Гидравлика_практ.doc
• Тип: Методические указания; #11548
• страница: 2 из 7

3. Гидравлический расчет коротких трубопроводов

Рассмотрим установившееся движение жидкости в напорных трубопроводах при постоянном напоре.

При движении реальных жидкостей в трубопроводах происходят потери напора (удельной энергии), которые в соответствии с законом наложения сопротивлений определяются между двумя расчетными сечениями 1-1 и 2-2 как сумма:

, (3.1)

где - сумма потерь напора на преодоление местных сопротивлений;

- сумма потерь напора по длине (на трение).

Все трубопроводы, работающие в напорном гидравлическом режиме, по принятой классификации делят на три вида:

1. Насадки - весьма короткие трубы, длина которых находится в пределах

. (3.2)

При гидравлическом расчете насадков учитываются только местные потери напора, потерями напора по длине ввиду их малости пренебрегают.

2. Короткие трубопроводы - трубопроводы, в которых местные потери напора и потери по длине сопоставимы по значению, поэтому при гидравлическом расчете коротких трубопроводов учитываются все потери напора как местные, так и по длине.

3. Длинные трубопроводы - трубопроводы, в которых потери напора по длине настолько превышают местные потери, что последними, ввиду малости, пренебрегают или учитывают долей в общих потерях, увеличивая найденные значения потерь напора по длине на 5-10 %.

Главнейшими уравнениями, которые применяются для расчета насадков и коротких трубопроводов, являются:

1) уравнение Бернулли для целого потока реальной жидкости;

2) уравнение неразрывности или баланса расхода;

3) уравнения для определения потерь напора.

В зависимости от исходных данных и методики расчета коротких трубопроводов различают три типа задач:

1) определение напора , необходимого для пропуска расчетного расхода в трубопроводе заданных размеров;

2) определение расхода при расчетном напоре в заданном трубопроводе;

3) определение диаметра трубопровода, обеспечивающего пропуск расчетного расхода при заданном напоре .

Часто в числе задач гидравлического расчета коротких трубопроводов требуется выполнить построение напорной (линии удельной энергии) и пьезометрической линий.

Следует отметить, что с гидравлической точки зрения к коротким трубопроводам (трубам) относятся все сооружения трубчатой конструкции, работающие в напорном гидравлическом режиме.

Основным уравнением гидродинамики, устанавливающим связь между основными характеристиками потока - скоростью, давлением в двух выбранных сечениях 1-1 и 2-2, является уравнение Бернулли:

. (3.3)

Каждый член, входящий в уравнение Бернулли, с геометрической и энергетической точек зрения имеет определенный смысл.

Геометрическая интерпретация уравнения Бернулли:

- высота положения, произвольно выбранной в рассматриваемом живом сечении, точки относительно любой горизонтальной плоскости сравнения 0 - 0; за характерную точку в большинстве случаев принимается центр тяжести сечения и тогда - высота положения сечения над плоскостью сравнения (геодезическая высота), определяется расстоянием от плоскости сравнения до центра тяжести сечения;

- пьезометрическая высота, соответствующая избыточному давлению в точке;

пьезометрический напор;

- скоростной напор;

гидродинамический напор;

- потери напора.

Энергетическая интерпретация уравнения Бернулли:

- удельная энергия положения;

- удельная энергия давления;

- удельная потенциальная энергия;

- удельная кинетическая энергия;

- полная удельная энергия;

- потери полной удельной энергии.

Слово «удельная » в энергетической интерпретации означает, что каждый член уравнения Бернулли отнесен к единице веса жидкости, проходящей через живое сечение в единицу времени.

Уравнение Бернулли может быть применено к потоку, только при выполнении трех условий:

1. Расход жидкости между двумя сечениями 1-1 и 2-2, из которых первое всегда располагается выше по течению, должен быть постоянным (Q=const).

2. Движение жидкости должно быть установившемся.

3. Движение жидкости в сечениях 1-1 и 2-2 должно быть параллельноструйным или плавноизменяющимся; в промежутке между выбранными сечениями движение может быть и резко изменяющимся.

В уравнении (3.3) коэффициент кинетической энергии (коэффициент Кориолиса) равен отношению действительной кинетической энергии потока, имеющего в живом сечении эпюру распределения скоростей, к кинетической энергии, вычисленной по средней скорости в живом сечении . По опытным данным при турбулентном прямолинейном движении воды в трубах .

Удельная энергия потока (гидродинамический напор) при движении реальной жидкости уменьшается в направлении движения от первого сечения ко второму. Поэтому, откладывая каждый раз (в расчетных сечениях по длине) от горизонтальной плоскости 0-0 величину в сечениях, получим напорную линию , уклон которой на прямолинейных участках трубопровода есть гидравлический уклон:

. (3.4)

Ниже линии на расстоянии от плоскости сравнения равном (или от линии на расстоянии ) располагается пьезометрическая линия , уклон которой называется пьезометрическим

, (3.5)

причем величина уклона может быть 0>>0, а в частном случае и равна нулю.

Если при построении пьезометрическая линия на некотором участке располагается ниже оси трубопровода, то это значит, что на участке давление меньше атмосферного, т.е. наблюдается вакуум. Разность между ординатами рассматриваемой точки сечения и пьезометрической линии на данной вертикали соответствует величине вакуума , выраженного в водяного столба.

В зависимости от положения уровня воды на выходе различают свободное и затопленное истечение из коротких трубопроводов. При свободном незатопленном истечении местные потери напора на выходе потока из грубы будут равны нулю, а пьезометрическая линия приходит к центру выходного сечения. При затопленном истечении потери напора на выход имеют место и определяются как на внезапное расширение, а линия приходит к отметке уровня воды на выходе.

Кроме уравнения Бернулли, к основным, которые используются при расчете коротких трубопроводов, относятся и другие зависимости, в том числе основное уравнение расхода, уравнение неразрывности, формулы Вейсбаха и Дарси - Вейсбаха.

Основное уравнение для расхода

, (3.6)

откуда

, (3.7)

где - площадь живого сечения;

- средняя скорость в живом сечении.

Уравнение неразрывности или баланса расхода:

. (3.8)

Потери напора по длине, обусловленные вязкостью жидкости и шероховатостью поверхности труб, вычисляются по формуле Дарси-Вейсбаха:

, (3.9)

где - коэффициент гидравлического трения или коэффициент Дарси.

Исследованиями зависимости коэффициента 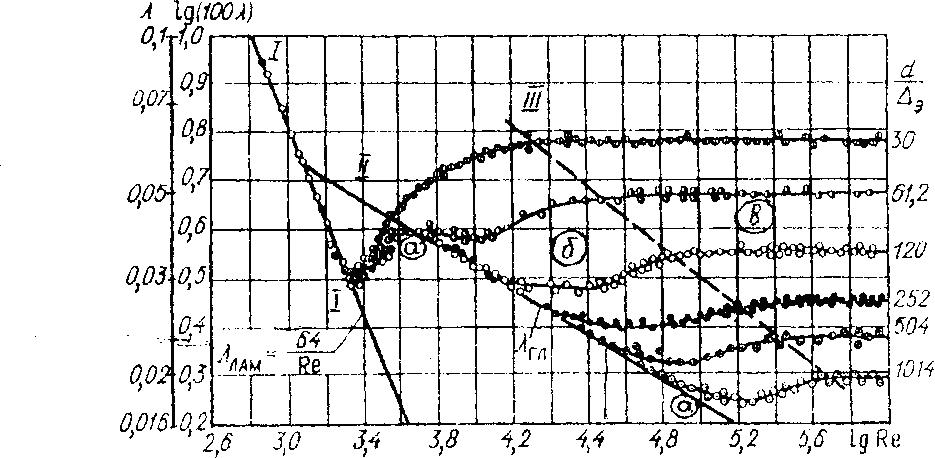, выполненными Никурадзе (рисунок 2.1) и др., установлены три зоны сопротивлений - зона ламинарного, переходного и турбулентного режима. Зона турбулентного режима, в свою очередь, подразделяется на три области - область гидравлически гладких русел (труб), доквадратичная и квадратичная области сопротивлений.

Рисунок 3.1 - График Никурадзе для труб с однородной равнозернистой шероховатостью

I - Зона ламинарного режима; II - Зона переходного режима; III - Зона турбулентного режима;

прямая a-a - область гидравлически гладких русел; б - доквадратичная область сопротивлений;

в - квадратичная область сопротивлений
Коэффициент трения, в общем случае зависящий от числа Рейнольдса и относительной шероховатости , где - эквивалентная шероховатость, может определяться по графикам, которые приводятся в справочной литературе [7-9], или с помощью эмпирических формул, полученных для разных зон и областей сопротивлений (см. ниже).

Металлические, железобетонные и другие трубы, используемые на практике, имеют неоднородную, разнозернистую (техническую) шероховатость, которая оценивается некоторой средней высотой выступов, называемой эквивалентной шероховатостью. Под эквивалентной шероховатостью понимают высоту выступов равнозернистой шероховатости из однородного песка, при которой в квадратичной области сопротивления получается такое же значение коэффициента трения , что и в рассматриваемой трубе. Числовые значения , приводятся в справочной литературе [7-9].

Для зоны ламинарного режима при коэффициент трения зависит от числа Рейнольдса и определяется по формуле:

, (3.10)

где - число Рейнольдса;

- кинематическая вязкость, зависящая от рода жидкости и ее температуры Т°С (табл. П1).

Зона переходного режима (неустойчивых режимов) имеет небольшой диапазон изменения чисел Рейнольдса. Здесь , но зависимость сложная и в учебном процессе не рассматривается.

При турбулентном режиме в области гидравлически гладких труб (русел), когда

, (3.11)

коэффициент трения зависит только от числа Рейнольдса и определяется по формуле Блазиуса (1913 г.):

. (3.12)

Для турбулентного режима движения в доквадратичной области сопротивления, когда

, (3.13)

коэффициент трения зависит и от числа Рейнольдса и от относительной шероховатости. Для этой области сопротивления может быть рекомендована формула А.Д. Альтшуля:

. (3.14)

Наиболее значимой для гидравлических расчетов является квадратичная область сопротивлений, которая наступает при числах Рейнольдса

. (3.15)

В этой области коэффициент зависит только от относительной шероховатости и может определятся по формуле Б.Л. Шифринсона:

. (3.16)

Местные потери напора в общем случае вычисляются по формуле Ю. Вейсбаха:

. (3.17)
где - коэффициент местного сопротивления, зависящий от вида местного сопротивления.

Численные значения коэффициентов , полученные, как правило, в результате экспериментальных исследований, кроме случая внезапного расширения, приведены в справочной литературе [7-9].

Коэффициент сопротивления на вход в трубу при острых кромках равен =0,5.

При внезапном (резком) сужении от сечения до коэффициент сопротивления на внезапное сужение определяется по формуле:

. (3.18)

При внезапном расширении коэффициент сопротивления равен: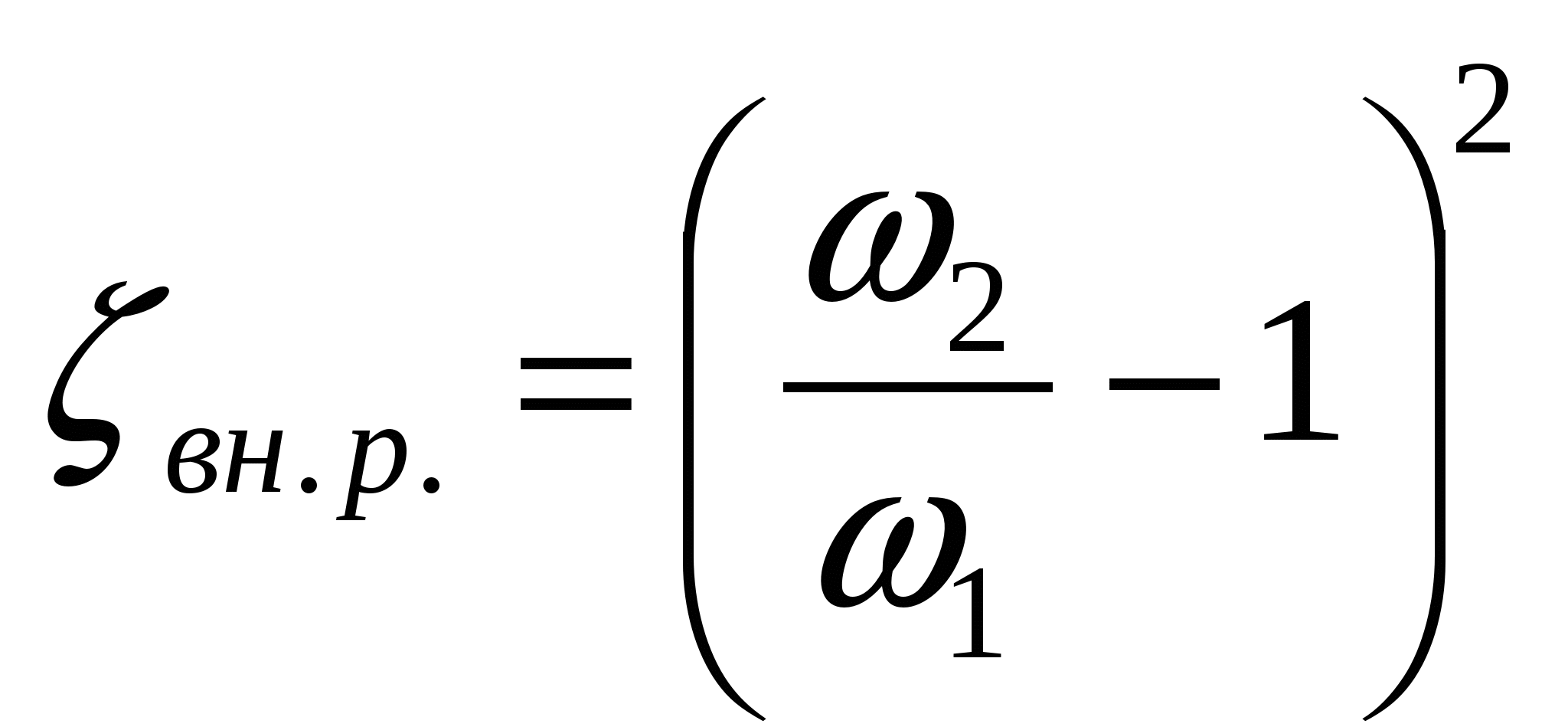

. (3.19)

При наличии на трубопроводе пробкового крана (схемы 1, 2) потери напора и коэффициент сопротивления крана зависят от угла его поворота (закрытия). Величина коэффициента для разных углов закрытия крана акр приведена,в таблице П2.

Потери напора при повороте трубы зависят от плавности и угла поворота трубы. В случае резкого поворота (колено) круглой или квадратной трубы коэффициент сопротивления принимается по таблице П3 в зависимости от угла поворота .

Коэффициент сопротивления на выход при затопленном истечении принимается =1.