физика Му к контрольным 2016. Методические указания к контрольным работам для студентов направления подготовки 21. 05. 04 Горное дело
 Скачать 453.28 Kb. Скачать 453.28 Kb.
|
|
Тело массой 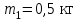 ударяется о неподвижное тело массой ударяется о неподвижное тело массой 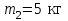 , которое после удара начинает двигаться с кинетической энергией , которое после удара начинает двигаться с кинетической энергией 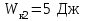 . Считая удар центральным и упругим, найти кинетическую энергию первого тела до и после удара. . Считая удар центральным и упругим, найти кинетическую энергию первого тела до и после удара.Человек массой 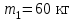 , бегущий со скоростью , бегущий со скоростью 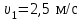 , догоняет тележку массой , догоняет тележку массой 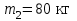 , движущуюся со скоростью , движущуюся со скоростью 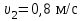 , и вскакивает на неё. Найти кинетическую энергию тележки с человеком и время движения до полной остановки, если коэффициент трения при движении тележки = 0,04. , и вскакивает на неё. Найти кинетическую энергию тележки с человеком и время движения до полной остановки, если коэффициент трения при движении тележки = 0,04.Шар массой 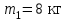 сталкивается с шаром массой сталкивается с шаром массой 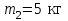 . Скорость первого шара . Скорость первого шара 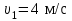 , второго – , второго – 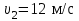 . Найти скорость шаров после удара и их кинетическую энергию, если шары движутся навстречу друг другу. Удар считать прямым, центральным, неупругим. . Найти скорость шаров после удара и их кинетическую энергию, если шары движутся навстречу друг другу. Удар считать прямым, центральным, неупругим.На железной платформе установлено орудие. Масса платформы с орудием 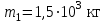 . Орудие стреляет под углом = 60 к горизонту в направлении железнодорожного пути. Какую кинетическую энергию получает орудие с платформой вследствие отдачи, если масса снаряда . Орудие стреляет под углом = 60 к горизонту в направлении железнодорожного пути. Какую кинетическую энергию получает орудие с платформой вследствие отдачи, если масса снаряда 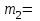 30 кг, и он вылетает со скоростью 500 м/с? 30 кг, и он вылетает со скоростью 500 м/с?Масса снаряда 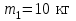 , масса ствола орудия , масса ствола орудия 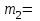 600 кг. При выстреле снаряд получает кинетическую энергию 600 кг. При выстреле снаряд получает кинетическую энергию 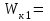 1,8·106 Дж. Определить кинетическую энергию, получаемую стволом орудия вследствие отдачи? 1,8·106 Дж. Определить кинетическую энергию, получаемую стволом орудия вследствие отдачи?Стержень длиной 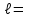 1,5 м и массой 1,5 м и массой 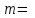 10 кг может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня. В середине стержня застревает пуля массой 10 кг может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня. В середине стержня застревает пуля массой 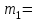 10 г, летевшая в горизонтальном направлении со скоростью 10 г, летевшая в горизонтальном направлении со скоростью 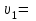 500 м/с. На какой угол отклонится стержень после удара? 500 м/с. На какой угол отклонится стержень после удара?Человек стоит на скамье Жуковского и ловит рукой мяч массой 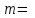 0,4 кг, летящий в горизонтальном направлении со скоростью 0,4 кг, летящий в горизонтальном направлении со скоростью 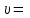 20 м/с. Траектория мяча проходит на расстоянии 20 м/с. Траектория мяча проходит на расстоянии 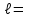 0,8 м от вертикальной оси Z вращения скамьи. С какой угловой скоростью ω начнет вращаться скамья Жуковского с человеком, поймавшим мяч? Считать, что суммарный момент инерции человека и скамьи 0,8 м от вертикальной оси Z вращения скамьи. С какой угловой скоростью ω начнет вращаться скамья Жуковского с человеком, поймавшим мяч? Считать, что суммарный момент инерции человека и скамьи 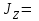 6 кг·м2. 6 кг·м2.На краю горизонтальной платформы, имеющей форму диска радиусом 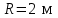 , стоит человек. Масса платформы , стоит человек. Масса платформы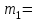 200 кг, масса человека 200 кг, масса человека 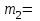 80 кг. Платформа может вращаться вокруг вертикальной оси, проходящей через её центр. Найти угловую скорость ω вращения платформы, если человек будет идти вдоль её края со скоростью 80 кг. Платформа может вращаться вокруг вертикальной оси, проходящей через её центр. Найти угловую скорость ω вращения платформы, если человек будет идти вдоль её края со скоростью 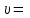 2 м/с относительно Земли? Трением пренебречь. 2 м/с относительно Земли? Трением пренебречь.Определить момент инерции проволочного равностороннего треугольника со стороной 0,1 м относительно оси, совпадающей с одной из сторон. Масса треугольника 12 г равномерно распределена по длине проволоки. Три маленьких шарика массой m = 10 г каждый расположены в вершинах равностороннего треугольника и скреплены между собой. Сторона треугольника а = 20 см. Определить момент инерции относительно оси: 1) перпендикулярной плоскости треугольника и проходящей через центр описанной окружности; 2) лежащей в плоскости треугольника и проходящей через центр описанной окружности и одну из вершин треугольника. Массой стержней, соединяющих шары, пренебречь. Вычислить момент инерции проволочного прямоугольника со сторонами а = 12 см, b = 16 см относительно оси, лежащей в плоскости прямоугольника и проходящей через середины малых сторон. Масса равномерно распределена по длине проволоки с линейной плотностью = 0,15 кг/м. Диаметр диска 20 см, масса 800 г. Определить момент инерции I диска относительно оси, проходящей через середину одного из радиусов перпендикулярно к плоскости диска. Длина одной стороны плоской однородной прямоугольной пластины а = 40 см, масса m = 800 г. Найти момент инерции пластины относительно оси, совпадающей со второй её стороной. Определить момент инерции тонкой плоской пластины со сторонами а = 10 см, b = 20 см относительно оси, проходящей через центр тяжести пластины параллельно большей стороне. Масса пластины равномерно распределена по её площади с поверхностной плотностью = 0,1 кг/м2. На конце тонкого стержня длиной = 60 см укреплен шарик массой m = 50 г. Пренебрегая размерами шарика, определить момент инерции системы относительно оси, перпендикулярной стержню и проходящей через его середину. Масса распределена вдоль стержня равномерно с линейной плотностью = 0,1 кг/м. Тонкий стержень длиной = 0,2 м и массой, равномерно распределённой с линейной плотностью = 0,2 кг/м, согнут пополам под прямым углом. Определить момент инерции стержня относительно оси, проходящей через конец стержня и лежащей в плоскости изогнутого стержня. Длина тонкого стержня = 0,6 м. Определить момент инерции стержня относительно оси, перпендикулярной к его длине и проходящей через точку стержня, удалённую на 0,2 м от одного из концов. Масса распределена равномерно с линейной плотностью = 0,15 кг/м. Определить момент инерции проволочного равностороннего треугольника со стороной а = 10 см относительно оси, лежащей в плоскости треугольника и проходящей через его вершину параллельно стороне, противоположной этой вершине. Масса треугольника равна 12 г и равномерно распределена по длине проволоки. Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек массой 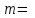 60 кг. На какой угол повернется платформа массой 60 кг. На какой угол повернется платформа массой 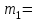 240 кг, если человек пойдет вдоль края платформы и, обойдя её, вернется в исходную точку на платформе? 240 кг, если человек пойдет вдоль края платформы и, обойдя её, вернется в исходную точку на платформе?Тонкий прямой стержень длиной 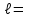 1 м может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня. Стержень отклонили на угол = 60 от положения равновесия и отпустили. Определить линейную скорость 1 м может вращаться вокруг неподвижной оси, проходящей через верхний конец стержня. Стержень отклонили на угол = 60 от положения равновесия и отпустили. Определить линейную скорость 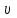 нижнего конца стержня в момент прохождения его через положение равновесия. нижнего конца стержня в момент прохождения его через положение равновесия.К стальному стержню длиной = 3 м и диаметром d = 2 см подвешен груз массой m = 2,5·103 кг. Определить напряжение в стержне, относительное и абсолютное удлинение стержня. Модуль Юнга для стали Е = 200 ГПа. Какой наибольший груз может выдержать стальная проволока диаметром 1 мм, если предел упругости 294 МПа? Какую долю первоначальной длины составляет удлинение проволоки при этом грузе? Пружина жёсткостью k = 500 Н/м сжата силой 100 Н. Определить работу внешней силы, дополнительно сжимающей пружину ещё на = 2 см. Какую работу А нужно совершить, чтобы пружину жёсткостью k= 800 Н/м, сжатую на 1 = 6 см, дополнительно сжать на 2 = 8 см. К вертикальной проволоке длиной = 5 м и площадью поперечного сечения S = 2 мм2 подвешен груз массой m = 5,1 кг. В результате проволока удлинилась на 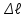 = 0,6 мм. Найти модуль Юнга E материала проволоки. = 0,6 мм. Найти модуль Юнга E материала проволоки.Вода течёт в горизонтально расположенной трубе переменного сечения. Скорость 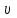 1 воды в широкой части трубы равна 20 см/с. Определить скорость 1 воды в широкой части трубы равна 20 см/с. Определить скорость 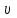 2 в узкой части трубы, диаметр d2 которой в 1,5 раза меньше диаметра d1 широкой части. 2 в узкой части трубы, диаметр d2 которой в 1,5 раза меньше диаметра d1 широкой части.Нижнее основание железного цилиндра диаметром d = 20 см и высотой h = 20 см закреплено неподвижно. На верхнее основание цилиндра действует горизонтальная сила F = 20 кН. Найти тангенциальное напряжение в материале, угол сдвига и смещение х верхнего основания цилиндра. Модуль сдвига для железа G =76 ГПа. Какой наибольший груз может выдержать стальная проволока диаметром d = 1 мм, если предел упругости упр = 294 МПа? Какую долю первоначальной длины составляет удлинение проволоки при этом грузе? Какая работа будет совершена силами гравитационного поля при падении на Землю из бесконечности тела массой m = 10 кг, если масса Земли МЗ = 5,98·1024 кг и её радиус RЗ = 6,37·106 м? С высоты h = 1000 км на поверхность Земли падает метеорит m = 30 кг. Определить работу А сил гравитационного поля Земли, если известны ускорение свободного падения у поверхности Земли g = 9,8 м/с2 и радиус Земли RЗ = 6,37·106 м. Определить импульс 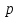 , полную , полную 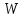 и кинетическую и кинетическую 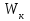 энергию нейтрона, движущегося со скоростью энергию нейтрона, движущегося со скоростью 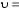 0,6 с. 0,6 с.Какую работу необходимо совершить, чтобы увеличить скорость частицы массой m0 от 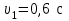 до до 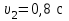 ? Сравнить полученный результат со значением, вычисленным ? Сравнить полученный результат со значением, вычисленнымпо классической формуле. Масса 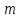 движущегося электрона вдвое больше его массы покоя m0. Найти кинетическую энергию движущегося электрона вдвое больше его массы покоя m0. Найти кинетическую энергию 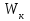 и импульс и импульс 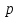 электрона. электрона.Найти скорость мезона, если его полная энергия 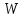 в 10 раз больше энергии покоя 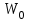 . .Какую долю скорости света должна составлять скорость 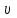 частицы, чтобы кинетическая энергия частицы, чтобы кинетическая энергия 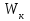 частицы была равна её энергии покоя частицы была равна её энергии покоя 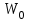 ? ?Синхрофазотрон даёт пучок протонов с кинетической энергией 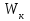 = 10 ГэВ. Какую долю скорости света в вакууме составляет скорость = 10 ГэВ. Какую долю скорости света в вакууме составляет скорость 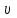 протонов в этом пучке? протонов в этом пучке?Циклотрон даёт пучок электронов с кинетической энергией 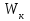 = 0,67 МэВ. Какова скорость = 0,67 МэВ. Какова скорость 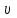 электронов в этом пучке? электронов в этом пучке?Какую ускоряющую разность потенциалов должен пройти электрон, чтобы его скорость составила 95 % скорости света в вакууме? Какую ускоряющую разность потенциалов должен пройти протон, чтобы его продольные размеры 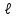 стали меньше стали меньшев два раза? Кинетическая энергия электрона 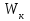 = 0,8 МэВ. Определить импульс = 0,8 МэВ. Определить импульс 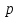 электрона. электрона.Найти среднюю кинетическую энергию 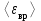 вращательного движения одной молекулы кислорода при температуре Т = 350 К, а также суммарную кинетическую энергию Wвр вращательного движения всех молекул, содержащихся вкислороде массой m = 4 г. вращательного движения одной молекулы кислорода при температуре Т = 350 К, а также суммарную кинетическую энергию Wвр вращательного движения всех молекул, содержащихся вкислороде массой m = 4 г.Найти среднюю кинетическую энергию 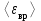 вращательного движения одной молекулы водорода, а также суммарную кинетическую энергию Wвр всех молекул, содержащихся вращательного движения одной молекулы водорода, а также суммарную кинетическую энергию Wвр всех молекул, содержащихсяв одном моле водорода при температуре Т = 190 К. Газ занимает объем V = 2 л под давлением р = 5·105 Па. Определить суммарную кинетическую энергию Wп поступательного движения молекул газа. Определить наиболее вероятную скорость 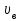 молекул газа при давлении р = 40 кПа, если при данных условиях его плотность молекул газа при давлении р = 40 кПа, если при данных условиях его плотность 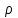 = 0,35 кг/м3. = 0,35 кг/м3.Колба емкостью V = 4 л содержит некоторый газ массой m = 0,6 г под давлением р = 2·105 Па. Определить среднюю квадратичную скорость 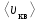 молекул газа. молекул газа.Коэффициент диффузии водорода при нормальных условиях D = 0,91 см2/с. Определить коэффициент теплопроводности водорода. Средняя длина 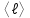 свободного пробега атомов гелия при нормальных условиях равна 1,8·10–7 см. Определить коэффициент диффузии D гелия при этих условиях. свободного пробега атомов гелия при нормальных условиях равна 1,8·10–7 см. Определить коэффициент диффузии D гелия при этих условиях.При нормальных условиях динамическая вязкость азота = 17 мкПа·с. Определить среднюю длину 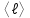 свободного пробега молекул газа. свободного пробега молекул газа.Азот находится под давлением p= 100 кПа при температуре T = 290 К. Определить коэффициент диффузии D и коэффициент внутреннего трения 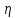 . Эффективный диаметр d молекул азота принять равным 0,38 нм. . Эффективный диаметр d молекул азота принять равным 0,38 нм.Определить плотность кислорода, если средняя длина свободного пробега его молекул 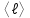 = 0,1 см. = 0,1 см.Водород занимает объем V = 10 м3 при давлении 105 Па. Газ нагрели при постоянном объёме до давления 3·105 Па. Определить изменение U внутренней энергии газа, работу А, совершаемую газом, и теплоту Q, сообщённую газу. Кислород нагревается при неизменном давлении р = 8·104 Па, при этом его объем увеличивается от V1 = 1 м3 до V2 = 3 м3. Определить изменение U внутренней энергии кислорода, работу А, совершаемую им при расширении, а также теплоту Q, сообщенную газу. Азот нагревался при постоянном давлении, причем ему была сообщена теплота Q = 2,1·105 Дж. Какую работу А совершил при этом газ? Каково было изменение U внутренней энергии? Азот массой m = 0,1 кг был изобарно нагрет от температуры Т1 =200 К до температуры Т2 =400 К. Определить работу А, совершенную газом, полученную им теплоту Q и изменение U внутренней энергии азота. Объем водорода при изотермическом расширении (Т = 300 К) увеличился в n = 3 раза. Определить работу А, совершенную газом, и теплоту Q, полученную им при этом. Масса водорода m = 200 г. При изотермическом расширении одного моля водорода, имевшего температуру Т = 300 К, затрачена теплота Q = 2 кДж. Во сколько раз увеличился объем газа? В цилиндре под поршнем находится азот массой 20 г. Газ был нагрет от температуры Т1 = 300 К до температуры 450 К при постоянном давлении. Определить теплоту Q, переданную газу, совершенную газом работу А и приращение U внутренней энергии. При изотермическом расширении водорода массой m = 1 г объем газа увеличился в два раза. Определить работу А расширения, совершенную газом, если температура газа 300 К. Определить теплоту Q, переданную при этом газу. 1 кмоль азота, находящегося при нормальных условиях, расширяется адиабатически от V1 до V2 = 5V1. Найти: 1) изменение внутренней энергии U газа; 2) работу A, совершенную при расширении. При адиабатическом расширении кислорода с начальной температурой t0 = 47 С внутренняя энергия уменьшилась на 8400 Дж. Определить массу m кислорода, если объем увеличился в 10 раз. КОНТРОЛЬНАЯ РАБОТА № 2 2.1–2.10. На рис. 3 показано распределение точечных зарядов 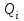 . Для заданных значений зарядов (табл. 5) определить силу, действующую на точечный заряд . Для заданных значений зарядов (табл. 5) определить силу, действующую на точечный заряд 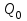 , помещенный в точку, указанную в последнем столбце, напряженность , помещенный в точку, указанную в последнем столбце, напряженность 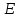 и потенциал и потенциал 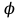 электростатического поля в этой точке. электростатического поля в этой точке.
|

 Q2
Q2