цвфавмы. Методические указания к лабораторным работам для студентов всех специальностей и направлений подготовки
 Скачать 7.09 Mb. Скачать 7.09 Mb.
|
|
Вопросы для подготовки к защите работы 1. Какова цель лабораторной работы? 2. Сколько характерных зон деформирования имеет диаграмма растяжения? 3. Как называют зоны деформирования диаграммы растяжения? 4. Что называют наклѐпом? Как изменяются механические свойства материала после наклѐпа? Как используют в технике явление наклѐпа? 5. По достижению какого напряжения появляется шейка на образце? 6. Как отличают истинное разрушающее напряжение от условного? 7. Для какого участка диаграммы справедлив закон Гука? 8. Что называется пределом пропорциональности? 9. Что называется пределом упругости? 10. Что называется пределом текучести? 11. Что называется площадкой текучести и при испытании каких материалов она бывает надиаграмме растяжения? 12. Покажите на диаграмме растяжения зону упругости и объясните ее суть. 13. Что называется пределом прочности? 14. Как определить параметры, характеризующие пластичность материала? 15. Что подразумевается под истинным напряжением? 2.2. Лабораторная работа №2. Определение модуля упругости и коэффициента Пуассона для стали Цель работы: изучение способа измерения модуля упругости и коэффициента Пуассона, определение упругих констант стали. 2.2.1. Теоретические основы При растяжении стержня в нем возникают продольные напряжения Zипродольные Z и поперечные X деформации. При растягивающих усилиях, соответствующих напряжениям, не превышающим предел текучести, продольные напряжения и деформации связаны соотношением, называемым законом Гука: 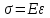 где Е — модуль упругости, который также называют модулем Юнга. Кроме продольных деформаций, в стержне возникают деформации в плоскости, перпендикулярной его оси (поперечные деформации), величину = εХ /εZ называюткоэффициентом Пуассона. При нагружении стержня в пределах упругой области коэффициент Пуассона является постоянной величиной и связь между продольными и поперечными деформациями в стержне линейна. 2.2.2. Экспериментальная часть. 1. Установить гидроцилиндр 2 на силовую раму стенда (рисунок 2.2.1) завернув два винта 1 и 3 на M10 с цилиндрической головкой и внутренним шестигранником. 2. Установить силоизмеритель на 50 кН с держателем (рисунок 2.2.2)на силовую раму стенда (рисунок 2.2.3).  Рисунок 2.2.1 Установка гидроцилиндра Наворачивание и затяжку гайки необходимо производить «от руки», применение гаечного ключа не требуется.  Рисунок 2.2.2 Монтаж силоизмерителя на 50 кН  Рисунок 2.2.3 Силоизмеритель на 50 кН с держателем 3. Измерить ширину b и толщинуt образца, вычислить площадь поперечного сеченияF0, занести данные в таблицу 2.2.1. 4. Установка образца показана на рисунке 2.2.4. Образец установить левой частью в вилку 1 с помощью пальца 2 (рисунок 2.2.4). После этого следует с помощью насоса сдвинуть гидроцилиндр в положение, обеспечивающее возможность установки пальца 9. Работа с насосом описана в пунктах 1.2.6 – 1.2.8. При необходимости повернуть вилку 10. Вращать вилку гидроцилиндра следует только по ходу часовой стрелки, если смотреть со стороны вилки.  Рисунок 2.2.4 Сборка стенда для проведения лабораторной работы №2 5. Установить (рисунок 2.2.4) микрометр 3 с цифровым выходом в держатель микрометра 5 и зафиксировать его с помощью винта 4. Установить второй держатель с упором микрометра. Расстояние между держателями для установки микрометра, измеряющего продольные перемещения, должно быть равно примерно 40 мм, а сами держатели должны быть параллельны. Установка держателей осуществляется путем затяжки стопорного винта 5 в середине пружинной части держателя. 6. После установки микрометра необходимо измерить рабочую длину l (расстояние между стопорными винтами двух опор), занести данные в таблицу 2.2.1. 7.Установить (рисунок 2.2.4) микрометр 6 в держатель для измерения поперечных перемещений, зафиксировав его с помощью винта 7. 8.Подключить разъемы силоизмерителя на 50 кН, микрометра и тензодатчиков, установленных на образце к измерительно- преобразовательному блоку. 9. Выполнить пункты 1.2.3 – 1.2.5. 10. В программе выбрать пункт меню «Тензометрирование». 11. Установить флажок напротив пункта «Определение упругих характеристик». Подождать пока значения деформаций (по тензорезисторам), отображаемые программой не перестанут меняться (произойдет прогрев тензоусилителей и тензорезисторов). Это может занять 5–10 минут. 12. В программе нажать кнопку «Балансировать деформации». 13. Перевести краны в положение, соответствующее втягиванию штока гидроцилиндра (рис. 1.2.3). 14.Обнулить показания микрометров, нажав кнопку «Zero». 15.Начать прикладывать нагрузку к образцу плавно вращая рукоятку привода насоса против часовой стрелки. Увеличить усилие, действующее на образец, на 3 кН. Текущее значение усилия следует наблюдать по программе «ОСМ измерения». 16.Записать значение усилия, показания микрометров (продольного ∆z и поперечного ∆Х) и значения деформации ZТР, ХТР, измеренных тензорезисторами в таблицу 2.2.1. Продольная деформация измеряется тензорезистором №2, поперечная - №1 (по обозначениям в программе «ОСМ измерения»). 17. Выполнить действия по п.п. 15 –16 до значения усилия в 27 кН. 18. Снять нагрузку с образца, для этого следует установить ручки обоих кранов вдоль корпусов. 19. Вынутьстопорные пальцы и снять образец. 20.Ослабить стопорные винты и демонтировать микрометры с образца. 21 .Демонтировать гидроцилиндр, силоизмеритель, и разложить все элементы на их места в ящиках и на стенде. Выключить питание измерительно-преобразовательного блока. Выйти из программы. 22. Рассчитать для каждого значения нагрузки значение действующего осевого напряжения б=P/F0, продольной εZ= ∆Z/l и поперечной εХ=∆Х/b деформации. Сравнить значения деформаций, полученные по микрометрам и по тензорезисторам. 23. Построить график зависимости б{∆Z), методом наименьших квадратов провести через полученные точки прямую линию и определить ее угловой коэффициент. Данный угловой коэффициент равен модулю упругости Е. Данное построение выполнить для деформаций определенных по микрометрам и по тензорезисторам. 24. Построить график зависимости εХ(εZ). Методом наименьших квадратов провести через полученные точки прямую линию и определить ее угловой коэффициент. Данный угловой коэффициент, взятый с обратным знаком, равен коэффициенту Пуассона (построение графиков и проведение прямой рекомендуется выполнять средствами Excel или аналогичных программ). Данное построение выполнить для деформаций определенных по микрометрам и по тензорезисторам.
Вопросы для подготовки к защите работы 1. Какова цель лабораторной работы? 2. Как записывают закон Гука при растяжении или сжатии в относительных параметрах? 3. Какие свойства материала характеризует модуль Юнга, коэффициент Пуассона? 4. Что называют базой рычажного тензометра? 5. С какой целью к образцу прикладывают начальную нагрузку? 6. Как определяется наибольшая нагрузка, прикладываемая к образцу? 7. Что собой представляет продольное растяжение - сжатие? 8. Напишите формулу для определения нормальных напряжений при продольном растяжении. 9. Как записывается формула абсолютного удлинения бруса при растяжении? Что такое жесткостьсечения бруса при растяжении? 10. Что происходит с поперечными размерами бруса при его растяжении в продольномнаправлении? 11. Что собой представляет относительная линейная деформация? 12. Что представляют собой относительная продольная и поперечная деформации? 13. Что такое коэффициент Пуассона? Каковы пределы его изменения? 14. Какие свойства материала характеризует коэффициент Пуассона? 15.Закон Гука при растяжении (сжатии). Связь каких величин отражает закон Гука? 2.3. Лабораторная работа №3. Определение модуля сдвига Цель работы: изучение способа испытаний материалов на чистый сдвиг, определение модуля сдвига стали. 2.3.1.Теоретические основы Существует такое напряженное состояние, когда на гранях выделенного элемента возникают только касательные напряжения (рисунок 2.3.1). Такое напряженное состояние называютчистым сдвигом. Кручением называется такой вид деформации, при котором в поперечных сечениях бруса возникает только один внутренний силовой фактор – крутящий момент Мк. Кручение возникает в валах, винтовых пружинах и других элементах конструкций. Кручение прямого бруса происходит при нагружении его внешними скручивающими моментами Мк (парами сил), плоскости действия которых перпендикулярны к его продольной оси. При кручении бруса круглого поперечного сечения в его сечениях возникают только касательные напряжения. 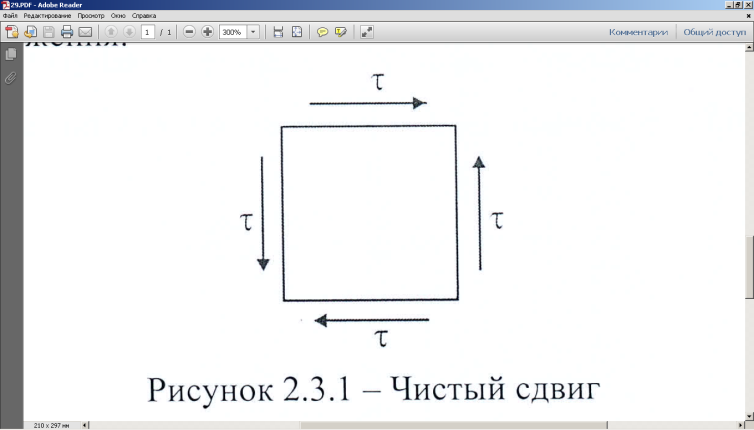 Рисунок 2.3.1 Чистый сдвиг Экспериментально однородный чистый сдвиг может быть осуществлен нагружением тонкостенной цилиндрической трубки моментами, приложенными в торцевых плоскостях (рисунок 2.3.2). Величина касательных напряжений определяется зависимостью (рис.2.3.3): 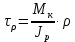 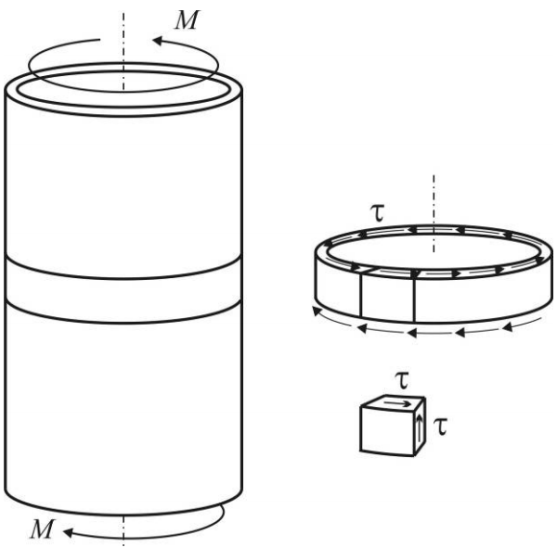 к к Рисунок 2.3.2 Кручение тонкостенной трубы Касательное напряжение связано с углом сдвигав пределах упругих деформаций соотношением: 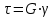 где G- модуль сдвига или модуль упругости второго рода: 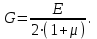 Он характеризует жесткость материала при деформации сдвига в результате возникающих деформаций торцовые сечения трубки (рисунок2.3.3)поворачиваются на некоторый угол, называемый углом закручивания. Характер возникающих смещений показан на рисунке2.3.3, причем 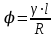 . .Для случая трубы со стенкой конечной толщины взаимный угол закручивания двух сечений, расположенных на расстоянии l определяется следующим образом: 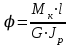 где JP- полярный момент инерции сечения трубы. 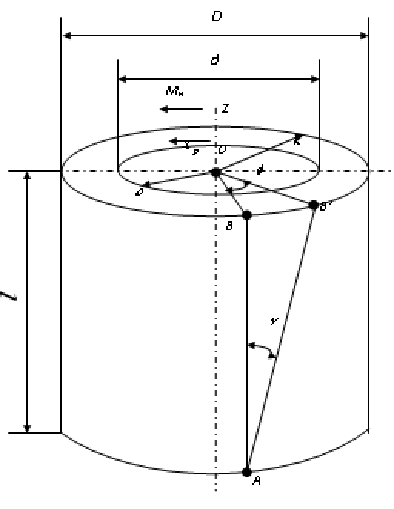 Рисунок 2.3.3 Перемещения при кручении Для случая трубы с внутренним диаметром dи внешним D: 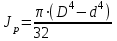 Взаимный угол поворота двух сечений может быть определен как разность двух углов поворота каждого из сечений относительно некоторого неподвижного основания, тогда 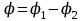 . .Если к скручиваемой трубе радиально прикрепить тонкий стержень (рисунок 2.3.4), то при малых углах поворота величина угла поворота может быть определена следующим образом: 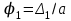 . .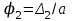 . .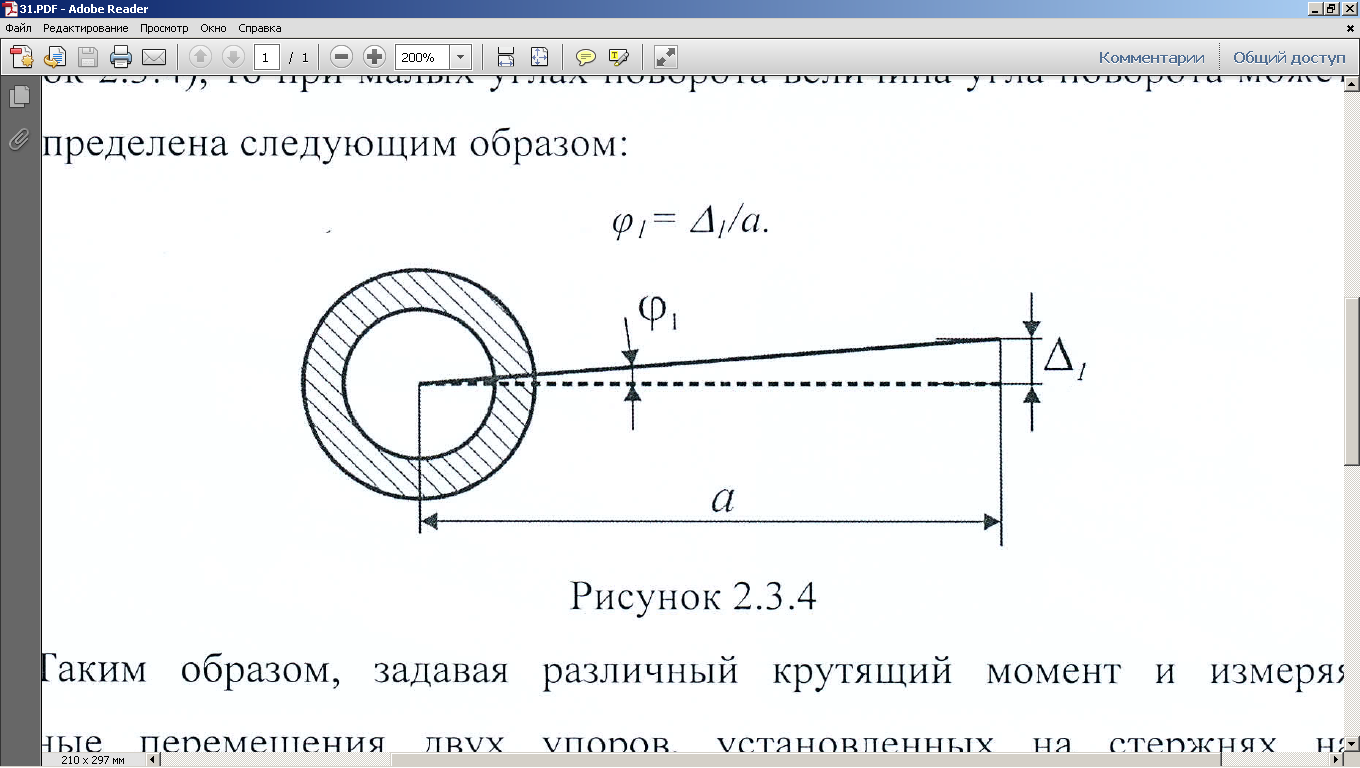 Рисунок 2.3.4 Схеме к расчету угла поворота Таким образом, задавая различный крутящий момент и измеряя линейные перемещения двух упоров, установленных на стержнях на расстоянии а от оси трубы, можно определить модуль сдвига материала трубы по следующей формуле: 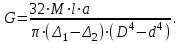 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
