Исследование логических схем. Методические указания к лабораторным занятиям УланУдэ 20220226. Оглавлени
 Скачать 347.95 Kb. Скачать 347.95 Kb.
|
|
Министерство образования и науки Российской Федерации Бурятский государственный университет Л.М. Макшанова С.А. БадмаеваМикропроцессорные системы МЕТОДИЧЕСКИЕ УКАЗАНИЯ к лабораторным занятиям Улан-Удэ 2022-02-26 .ОГЛАВЛЕНИ ПРАВИЛА ВЫПОЛНЕНИЯ ЛАБОРАТОРНЫХ РАБОТ 3 ОФОРМЛЕНИЕ ОТЧЁТОВ 4 ЛАБОРАТОРНАЯ РАБОТА №1 Исследование логических элементов интегральных микросхем (ИМС) серии К155 транзисторно-транзисторной логики (ТТЛ) 6 1. Цель работы: 6 2. Предварительная подготовка к работе: 6 3. Контрольные вопросы: 6 4. Порядок выполнения работы: 6 5. Теоретическая часть: 10 6.Содержание отчета: 19 7.Тест: 19 ПРАВИЛА ВЫПОЛНЕНИЯ ЛАБОРАТОРНЫХ РАБОТ 3 ОФОРМЛЕНИЕ ОТЧЁТОВ 3 ЛАБОРАТОРНАЯ РАБОТА №1 Исследование логических элементов интегральных микросхем (ИМС) серии К155 транзисторно-транзисторной логики (ТТЛ) 5 1. Цель работы: 5 2. Предварительная подготовка к работе: 5 3. Контрольные вопросы: 5 4. Порядок выполнения работы: 5 5. Теоретическая часть: 9 6.Содержание отчета: 18 7.Тест: 18 ПРАВИЛА ВЫПОЛНЕНИЯ ЛАБОРАТОРНЫХ РАБОТВыполнению каждой лабораторной работы предшествует самостоятельная предварительная подготовка студента путём изучения по литературе необходимых разделов курса, выполнения расчётов, изучения описания лабораторного макета, задания и порядка выполнения соответствующей лабораторной работы. Подготовленный студент должен также отчётливо представлять, что и как он будет делать, и какие результаты ожидаются в каждом из пунктов работы (мысленный эксперимент). В начале лабораторного занятия каждый студент представляет преподавателю рабочий листок с результатами предварительной подготовки по выполняемой работе: расчетами, схемами отдельных измерений по каждому пункту лабораторного задания. К выполнению работы допускаются только подготовленные студенты. Поэтому в начале занятия преподаватель проводит проверку готовности каждого студента путем устного собеседования или с помощью технических средств в объеме материала, указанного в описании лабораторной работы. Студенты, не допущенные к выполнению лабораторной работы, остаются в лаборатории для дополнительной подготовки. В процессе выполнения работы результаты эксперимента аккуратно оформляются в рабочих листках в виде таблиц, графиков. Результаты каждого пункта должны иметь соответствующие заголовки и пояснения исходных данных, режимов измерений. По окончании работы студент (бригада) представляет рабочий листок преподавателю для проверки и отметки о выполнении в журнале. Самовольный уход студентов из лаборатории не допускается. По результатам лабораторной работы каждый студент должен оформить отчёт и защитить работу. Студенты, хорошо подготовившиеся к работе и успешно выполнившие её, могут защитить эту работу в конце занятия (при наличии времени) по рабочим листкам без последующего оформления отчёта. При выполнении работы не рекомендуется часто включать и выключать питание электронных приборов. Питание всех приборов, применяющихся в лабораторной работе, выключается студентами только после выполнения всех пунктов лабораторного задания с разрешения преподавателя. Студенты, пропустившие лабораторное занятие без уважительной причины или не допущенные к выполнению лабораторной работы, выполняют её в специально установленное время (как правило, в конце семестра). При выполнении лабораторных работ необходимо соблюдать правила техники безопасности. Рабочее место в лаборатории должно быть оставлено в полном порядке: приборы должны стоять на положенных местах, провода аккуратно сложены, стулья ставятся вплотную к столу. ОФОРМЛЕНИЕ ОТЧЁТОВОтчёт по лабораторной работе должен содержать: название лаборатории; фамилию и инициалы студента; номер группы; наименование работы; номер лабораторной работы; предварительные расчеты; алгоритм исследования; результаты измерений в виде таблиц, графиков и расчётов; выводы по работе и оценку результатов; дату выполнения работы и личную подпись. При выполнении отчёта не следует переписывать с начала все пункты лабораторного задания, а затем приводить таблицу с результатами всех измерений. Результаты различных измерений необходимо представить в виде нескольких самостоятельных таблиц и графиков. Каждая таблица и каждый график должны иметь свой заголовок и исходные данные эксперимента. При выполнении численных расчетов надо записать формулу определяемой величины, сделать соответственную численную подстановку и произвести вычисления, а не писать сразу готовый результат. Результаты со всеми промежуточными вычислениями сложных нелинейных зависимостей следует приводить в виде таблицы. Все графики необходимо выполнять на миллиметровой бумаге или обычной бумаге в клетку. Оси координат на графиках должны быть обозначены и масштабированы. Масштаб следует выбирать таким образом, чтобы координаты любой точки графика могли быть определены быстро и с удовлетворительной точностью. Нанесение на графике точек, соответствующих расчетным или экспериментальным данным, должно быть выполнено отчетливо и аккуратно. Кривая, проводимая через экспериментальные точки, должна быть плавной, без резких искривлений и углов. Кривая не обязательно должна проходить через каждую отдельную точку. Её следует провести через большую часть точек так, чтобы наилучшим образом аппроксимировалась экспериментальная зависимость. Если на графике имеется несколько кривых, каждая кривая должна быть снабжена соответствующими надписями. Осциллограммы, характеризующие один и тот же процесс, например, напряжение на входе и выходе четырехполюсника, следует располагать строго друг под другом с общим началом отсчета и с соблюдением масштабов по осям координат. То же относится и к спектральным диаграммам. Необходимо пользоваться общепринятыми условными обозначениями величин и сокращениями названий. ЛАБОРАТОРНАЯ РАБОТА №1 1. Цель работы:1.1. Ознакомление с интегральными микросхемами (ИМС) ТТЛ серии К155, соответствие ИМС американской серии NS74 и российской серии К155. 1.2. Исследование логических схем «И2», «И-НЕ», «ИЛИ2», «ИЛИ-НЕ», «исключающее ИЛИ». 2. Предварительная подготовка к работе:2.1. Изучить следующие вопросы: а) ИМС серии 155, условные графические обозначения; б) Аналоги ИМС серии К155 и NS74 и их соответствие; 2. Составление таблицы истинности для логических элементов «И», «И-НЕ», «ИЛИ», «ИЛИ-НЕ», «исключающее ИЛИ». 3. Контрольные вопросы:Кроме таблицы истинности, какие дополнительные формы отображения основных логических функций существуют? Что такое логическая функция? Что такое логический элемент? Какие устройства называются логическими или цифровыми? Каким образом удобно проводить анализ комбинационных схем? Для логических элементов «И», «И-НЕ», «ИЛИ», «ИЛИ-НЕ», «исключающее ИЛИ» указать ИМС ТТЛ серии К155 и их зарубежные аналоги. Для логических элементов «И», «И-НЕ», «ИЛИ», «ИЛИ-НЕ», «исключающее ИЛИ» указать условные графические обозначения. 4. Порядок выполнения работы:Загрузить программу «Multisim» и выполнить все пункты задания. Собрать схему 1 для исследования логического элемента «2И-НЕ» (рис.1.). 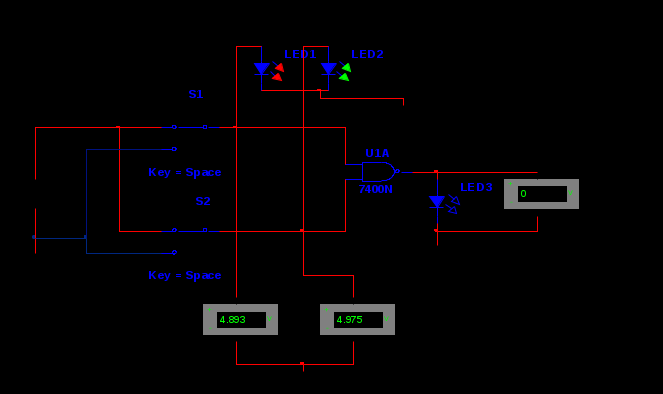 Рис.1. Исследование логического элемента 2И-НЕ (ИМС К155ЛА3) 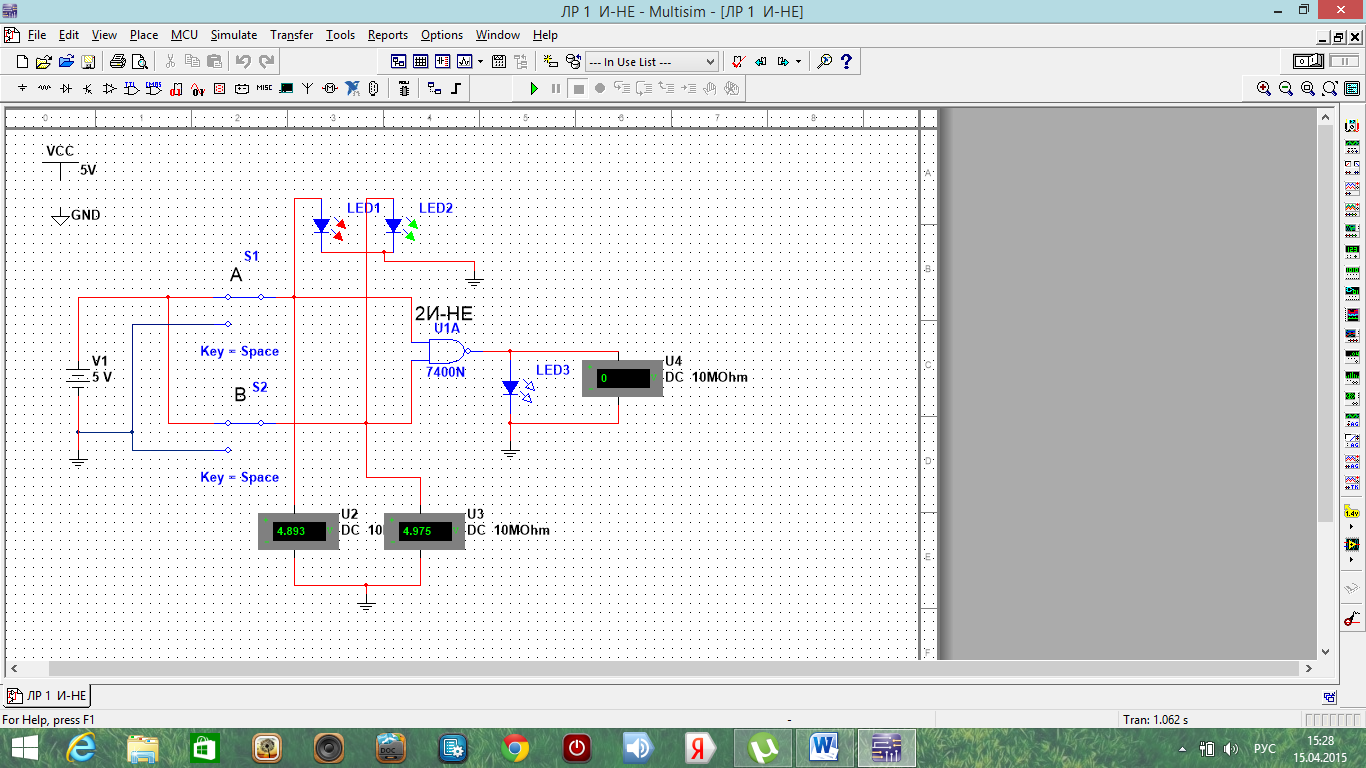 Рис. 2. Исследование логического элемента 2И-НЕ при А=В=1 Схема 1 содержит исследуемую функцию «И-НЕ» ИМС К155ЛА3 (7400N) - элемента И-НЕ с 2 входами, два двухпозиционных переключателя (S1, S2), управляемые клавишами А и В (заглавные буквы латинского алфавита), источники сигналов логической единицы (+5 В источника постоянного напряжения), логического нуля (0 В - заземление источника постоянного напряжения), три светодиода (A, B, Q), три вольтметра, источник постоянного напряжения 5В (VCC) для питания интегральной микросхемы, электронное заземление (GND). Выполнить следующие действия: Запустить процесс моделирования. Подать на входы схемы «И-НЕ» все возможные комбинации уровней сигналов А и В с помощью переключателей S1 и S2. Для каждой комбинации зафиксировать показания вольтметров и уровни входных сигналов А и В, уровень выходного сигнала Q (логическая единица – соответствующий светодиод светится, логический ноль – соответствующий светодиод не светится). Результаты измерений занести в таблицу истинности (табл. 1). Собрать схему 2 с логическим элементом «И», предварительно выбрав зарубежный аналог 7408N для данного элемента ИМС серии 155 и результаты измерений занести в таблицу 1. 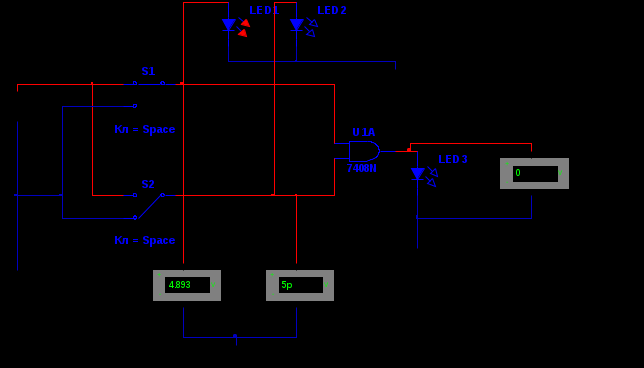 Рис.3. Исследование логического элемента И (ИМС К155ЛИ1) Собрать схему 3 с логическим элементом «ИЛИ-НЕ», предварительно выбрав зарубежный аналог 7402N для данного элемента ИМС серии 155 и результаты измерений занести в таблицу 1. 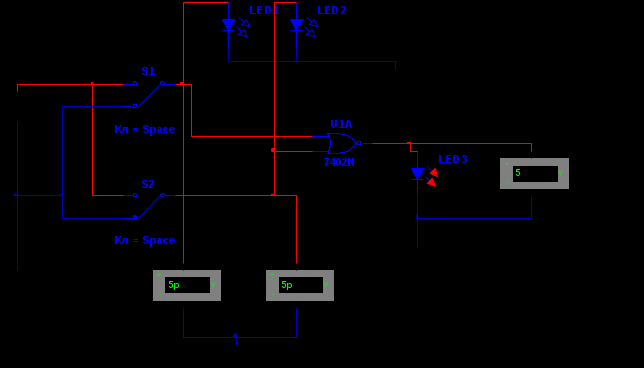 Рис.4. Исследование логического элемента ИЛИ-НЕ (ИМС К155ЛЕ1) Собрать схему 4 с логическим элементом «ИЛИ», предварительно выбрав зарубежный аналог 7432N для данного элемента ИМС серии 155 и результаты измерений занести в таблицу 1. 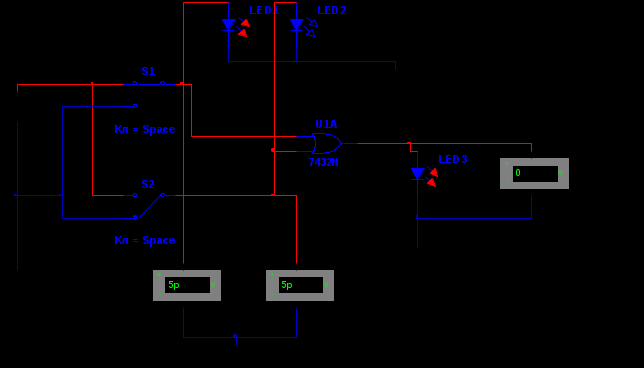 Рис.5. Исследование логического элемента ИЛИ (ИМС К155ЛЛ1) Собрать схему 5 с логическим элементом «Исключающее ИЛИ», предварительно выбрав зарубежный аналог 7486N для данного элемента ИМС серии 155 и результаты измерений занести в таблицу 1. 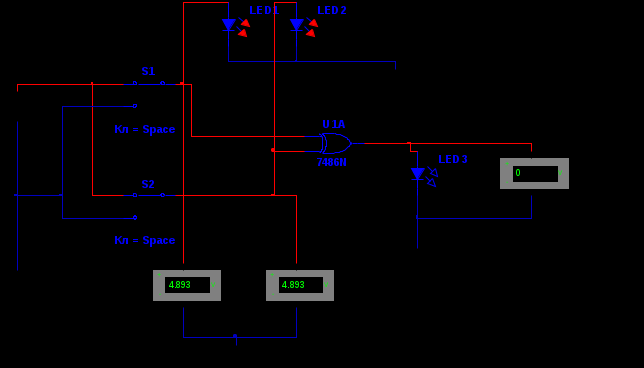 Рис.6. Исследование логического элемента «исключающее ИЛИ» (ИМС К155ЛП5) Т а б л и ц а 1 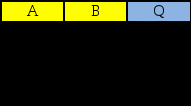 5. Теоретическая часть:Аксиомы алгебры логики Переменные, рассматриваемые в алгебре логики, могут принимать только два значения: ноль или единица. В алгебре логики определены: отношение эквивалентности, обозначаемое знаком =; операция сложения (дизъюнкция), обозначаемая знаком + или ; операция умножения (конъюнкция), обозначаемая знаком & или *; операция отрицания (или инверсия), обозначаемая знаком надчеркивания или апострофом ’. Алгебра логики определяется следующей системой аксиом: x = 0, если х  1, 1, 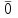 = 1, = 1,x = 1, если х 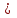 0, 0, 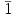 = 0, = 0,1+ 1 = 1, 0 * 0 = 0, 0 + 0 = 0, 1 * 1 = 1, 0 + 1 = 1 + 0 = 1, 1 * 0 = 0 * 1 + 0. Логические выражения Логические выражения связывают значение логической функции со значениями логических переменных. Они могут записываться в конъюнктивной или дизъюнктивной нормальных формах. В дизъюнктивной форме логические выражения записываются как логическая сумма логических произведений, в конъюнктивной – как логическое произведение логических сумм. Порядок действий в логических выражениях такой же, как и в обычных алгебраических выражениях. Логические выражения связывают значение логической функции со значениями логических переменных. Законы булевой алгебры Они вытекают из аксиом и имеют две формы выражения: для конъюнкции и дизъюнкции. Эти законы используются при преобразованиях логических выражений. Переместительный закон: 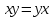 ; ; 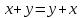 ; ;сочетательный закон: 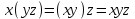 ; ; 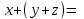 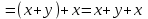 ; ;распределительный закон: 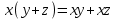 ; ; 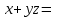 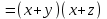 ; ; закон повторения: 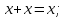 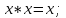 закон обращения: если 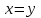 , то , то 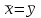 ; ;закон двойной инверсии: 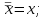 закон универсального множества: 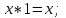 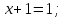 закон дополнительности: 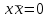 ; ; 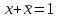 ; ;закон нулевого множества: 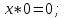 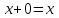 ; ;закон поглощения: 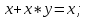 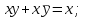 закон склеивания: 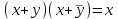 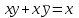 ; ;закон инверсии (закон Де Моргана): 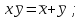 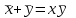 . .Логические функции Любое логическое выражение, составленное из nпеременных xn,,xn-1, …,x1c помощью конечного числа операций алгебры логики, можно рассматривать как некоторую функцию n переменных, называемую логической. В соответствии с аксиомами алгебры логики функция может принимать в зависимости от значения переменных значение 0 или 1. Функция n логических переменных может быть определена для 2n значений переменных, соответствующих всем возможным значениям n-разрядных двоичных чисел. Основной интерес представляют следующие функции двух переменных xи y: f1(x,y) = x*y – логическое умножение, f2(x,y) = x + y – логическое сложение, f3(x,y) = 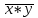 – логическое умножение с инверсией, – логическое умножение с инверсией,f4(x,y) = 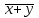 – логическое сложение с инверсией, – логическое сложение с инверсией,f5(x,y) = 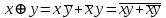 – суммирование по модулю два или «Исключающее ИЛИ», – суммирование по модулю два или «Исключающее ИЛИ»,f6(x,y) = 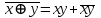 – равнозначность. – равнозначность.Логические схемы Физическое устройство, реализующее одну из операций алгебры логики или простейшую логическую функцию, называется логическим элементом. Схема, составленная из конечного числа логических элементов по определенным правилам, называется логической. Основным логическим функциям соответствуют выполняющие их схемные элементы. Например, функции f1(x,y) соответствует логическая схема «И», функции f2(x,y) – логическая схема «ИЛИ», функции f3(x,y) – логическая схема «И-НЕ», функции f4(x,y) – логическая схема «ИЛИ-НЕ». Таблица истинности Так как область определения любой функции n переменных конечна (может принимать 2n значений), то такая функция может быть задана таблицей значений f(x), которые она принимает в точках xi, где i= 0,1, …, 2n-1. Такие таблицы называются таблицами истинности. В табл. 2 представлены значения функций f1(x,y), …, f6(x,y). Т а б л и ц а 2
Основные логические операции ИЛИ, И и НЕ позволяют аналитически описать, а логические элементы ИЛИ (дизъюнктор), И (конъюнктор) и НЕ (инвертор) реализовать комбинационное устройство любой степени сложности, т. е. операции 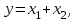 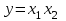 и и 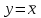 обладают функциональной полнотой и составляет функционально полный набор. обладают функциональной полнотой и составляет функционально полный набор. Условные графические обозначения (УГО) элементов цифровой техники содержит ГОСТ 2.743-91 ЕСКД. Обозначения условные графические в схемах. Элементы цифровой техники. Программа EWB поддерживает две системы условных графических обозначение (УГО) моделей электронных компонентов - ANSI и DIN. ANSI - это американский стандарт (American National Standart Institute), DIN - европейский стандарт (Deutsche Ingenieuring Normen - немецкий инженерный стандарт). Российский ГОСТ ближе к стандарту DIN. По умолчанию в EWB используется стандарт ANSI, но предусмотрена возможность перехода к стандарту DIN. Для этого при установке программы (Setup) в окне выбора компонентов (Select Components) следует выбрать опцию DIN. В противном случае ряд компонентов окажется с неузнаваемыми УГО, например, резистор будет похож на острозубую пилу, а индуктивность - на пружину от старого матраца. На принципиальных схемах логический элемент И обозначают как на рис.4. 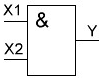 Рис.4. УГО логического элемента И (ГОСТ) На зарубежных схемах обозначение элемента "И" имеет другое условное графическое обозначение (Рис.5). Его кратко называют AND. 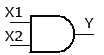 Рис.5. УГО логического элемента И (ANSI) На схемах элемент "ИЛИ" изображают как на рис.6. 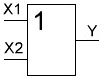 Рис.6. УГО логического элемента ИЛИ (ГОСТ) На зарубежных схемах его изображают чуть по-другому и называют элементом OR. 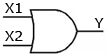 Рис.7. УГО логического элемента ИЛИ (ANSI) Логический элемент НЕ изображают на схемах (Рис.8). 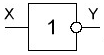 Рис.8. УГО логического элемента НЕ (ГОСТ) В зарубежной документации элемент "НЕ" изображают следующим образом. Сокращённо называют его NOT (Рис.9.). 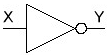 Рис.9. УГО логического элемента НЕ (ANSI) Логический элемент «Исключающее ИЛИ» изображается на схемах знаком равенства перед единицей "=1" (Рис.10). 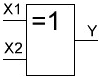 Рис.10. УГО логического элемента «исключающее ИЛИ» (ГОСТ) На зарубежный манер "исключающее ИЛИ" называют XOR и на схемах обозначают как на Рис.11. 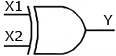 Рис.11. УГО логического элемента «исключающее ИЛИ» (ANSI) Транзисторно-транзисторная логика Интегральные микросхемы транзисторно-транзисторной логики (ТТЛ) получили широкое распространение благодаря сравнительно высокому быстродействию и надежности, технологичности изготовления, функциональной полноте серии ТТЛ элементов. Основной элемент ТТЛ представлен на рис.12. Вход интегральной схемы (ИС) представляет собой многоэмиттерный транзистор VT1. Отдельно такие транзисторы не выпускаются, а используются только в интегральных схемах. 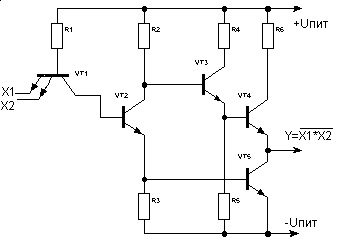 Рис.12. Базовый элемент 2И-НЕ ТТЛ Если на все его эмиттеры подать напряжения высокого уровня, то эмиттерный переход транзистора окажется закрытым. При этом ток. протекающий через резистор R1 и коллекторный переход транзистора VТ1, откроет транзистор VТ2. Падение напряжения на резисторе RЗ будет достаточным для открывания транзистора VТ5. Напряжение на коллекторе транзистора VТ2 таково, что транзистор VТЗ закрыт, соответственно закрыт и транзистор VТ4. В результате на выходе элемента появится напряжение низкого уровня, соответствующее логическому 0. Если же хоть на один из входов элемента подать напряжение низкого уровня, то эмиттерный переход транзистора VТ1 откроется, а транзисторы VТ2 и VТ5 будут закрыты. Транзистор VТЗ откроется за счет тока, протекающего через резистор R2, войдет в режим насыщения. Соответственно откроется транзистор VТ4, и на выходе элемента появится напряжение высокого уровня, соответствующее логической 1. Следовательно, рассмотренный элемент выполняет функцию И-НЕ. В состав микросхем серий ТТЛ входит также логический элемент И-НЕ без коллекторной нагрузки в выходном каскаде. Это так называемый элемент И-НЕ с открытым коллектором. Он предназначен для работы на внешнюю нагрузку, в качестве которой могут быть использованы электромагнитные реле, индикаторные приборы и т. д. Логические уровни ТТЛ микросхем В настоящее время применяются два вида ТТЛ микросхем — с пяти и с трёхвольтовым питанием, но, независимо от напряжения питания микросхем, логические уровни нуля и единицы на выходе этих микросхем совпадают. Поэтому дополнительного согласования между ТТЛ микросхемами обычно не требуется. Допустимый уровень напряжения на выходе цифровой ТТЛ микросхемы показан на рисунке 13. 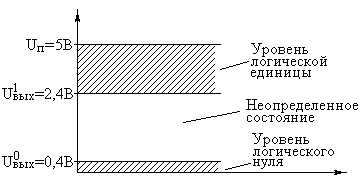 Рис.13. Уровни логических сигналов на выходе цифровых ТТЛ микросхем Как уже говорилось ранее, напряжение на входе цифровой микросхемы по сравнению с выходом обычно допускается в больших пределах. Границы уровней логического нуля и единицы для ТТЛ микросхем приведены на рисунке 14. 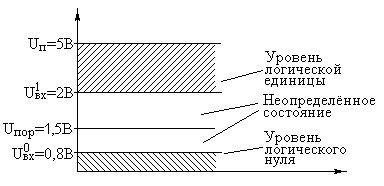 Рис. 14. Уровни логических сигналов на входе цифровых ТТЛ микросхем Семейства ТТЛ микросхем Промышленность выпускает интегральные схемы в пластмассовых, керамических или металлокерамических корпусах. Один из вариантов корпуса ИС приведен на рис. 15. С одной из сторон корпуса микросхемы нанесен ключ, от которого против хода часовой стрелки отсчитываются номера выводов.  Рис.15. Корпуса интегральных микросхем DIP (Dual In-line Package) Первые ТТЛ микросхемы оказались на редкость удачным решением, поэтому их можно встретить в аппаратуре, работающей до сих пор. Это семейство микросхем серии К155. Стандартные ТТЛ микросхемы — это микросхемы, питающиеся от источника напряжения +5 В. Зарубежные ТТЛ микросхемы получили название SN74. Конкретные микросхемы этой серии обозначаются цифровым номером микросхемы, следующим за названием серии. Например, в микросхеме SN74S00 содержится четыре логических элемента "2И-НЕ". Аналогичные микросхемы с расширенным температурным диапазоном получили название SN54 (отечественный вариант — серия микросхем К133). Отечественные микросхемы, совместимые с SN74 выпускались в составе серий К134 (низкое быстродействие низкое потребление — SN74L), К155 (среднее быстродействие среднее потребление — SN74) и К131 (высокое быстродействие и большое потребление). Затем были выпущены микросхемы повышенного быстродействия с диодами Шоттки. В названии зарубежных микросхем в обозначении серии появилась буква S. Отечественные серии микросхем сменили цифру 1 на цифру 5. Выпускаются микросхемы серий К555 (низкое быстродействие низкое потребление — SN74LS) и К531 (высокое быстродействие и большое потребление — SN74S). В настоящее время отечественная промышленность производит микросхемы серий К1533 (низкое быстродействие низкое потребление — SN74ALS) и К1531 (высокое быстродействие и большое потребление — SN74F). За рубежом производится трехвольтовый вариант ТТЛ микросхем — SN74ALB 6.Содержание отчета:Цель работы. Схемы для исследования логических элементов. Таблицы истинности логических элементов. Скриншоты, представляющие значение функции при определенном наборе входных данных. Ответы на контрольные вопросы. Выводы. 7.Тест:1. Укажите свойство, характеризующее основные логические элементы. На входах логических элементов аналоговые сигналы, а на выходах цифровые Операции логического сложения, логического умножения и инверсия не составляют функционально полный набор Используя основные логические операции И, ИЛИ и НЕ, можно аналитически выразить любую сложную логическую функцию На входах логических элементов цифровые сигналы, а на выходах аналоговые 2.Укажите логическое выражение логической функции двух переменных х1 и х2, реализуемой элементом конъюнктором. 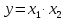 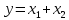 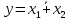 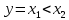 3.Укажите логическое выражение логической функции двух переменных х1 и х2, реализуемой элементом дизъюнктором. 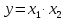 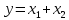 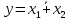 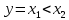 Укажите логическое выражение логической функции двух переменных х1 и х2, реализуемой элементом "Стрелка Пирса". 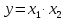 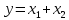 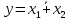 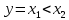 Укажите выражение логической функции двух переменных х1 и х2, реализуемой элементом "Штрих Шеффера". 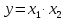 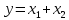 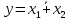 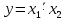 Логический элемент «Конъюнктор» выполняет операцию Логического умножения Логического сложения Логического отрицания Сложения Логический элемент «Исключающее ИЛИ» выполняет операцию Логического сложения Логического отрицания Логического умножения Сложения по модулю «2» Логический элемент «Инвертор» выполняет операцию Логического сложения Логического умножения Логического отрицания Вычитания Логический элемент «Дизъюнктор» выполняет операцию Логического сложения Логического умножения Сложения Умножения Может ли логический элемент «Инвертор» иметь количество входов Один Два Пять Десять | |||||||||||||||||||||||||||||||||||||||||||||||||||||
